
مدل آزاد توزیع برای مسئله مکان یابی آمبولانس با تقاضای مبهم
مشکل مکان یابی آمبولانس یک مسئله کلیدی در سیستم خدمات اورژانس پزشکی (EMS) برای تعیین موقعیت مکانی آمبولانس است تا با استفاده از آن بتوان به تماس های اضطراری به طور موثر پاسخ داد. بیشتر تحقیقات مربوطه بر مشکلات قطعی متمرکز هستند و یا فرض می کنند که توزیع احتمالی تقاضا را می توان برآورد کرد. با این حال در عمل، کسب اطلاعات کامل در مورد توزیع احتمال مشکل است. این مقاله، مسئله مکان یابی آمبولانس را با اطلاعات تقاضای جزئی مورد بررسی قرار می دهد؛ این به این معنی است که تنها ماتریس میانگین و کوواریانس خواسته ها شناخته شده اند. این مشکل شامل تعیین مکان های پایه و به کارگیری آمبولانس ها، برای به حداقل رساندن کل هزینه ها است. یک مدل آزاد توزیع جدید با محدودیت های شانسی پیشنهاد شده است. سپس دو فرمول برنامه ريزي عدد صحیح مختلط تقریب زده شده (MIP)، براي حل آن توسعه داده شده است. در نهایت، آزمایش های عددی بر روی معیارها (Nickel et al.، 2016) و 120 نمونه ایجاد شده به صورت تصادفی، انجام شده و نتایج محاسباتی نشان می دهد که این دو فرمول پیشنهادی ما می توانند یک سطح خدمات بالا در یک زمان کوتاه را تضمین کنند. به طور خاص، فرمول دوم هزینه کمتری را اتخاذ می کند، در حالی که یک سطح خدمات مناسب را تضمین می کند.
1. مقدمه
طراحی سیستم های خدمات اورژانس پزشکی (EMS) که سلامت و زندگی مردم را تحت تأثیر قرار می دهد، بر نحوه پاسخ سریع به موارد اضطراری متمرکز است. مشکل مکان یابی آمبولانس یکی از مشکلات کلیدی در سیستم EMS است که عمدتا شامل تعیین پایگاه هایی است که به عنوان امکانات خدمات اورژانس نیز نامیده شده است، و همچنین به کارگیری آمبولانس ها به منظور ارائه خدمات کارآمدتر در شرایط اضطراری و تضمین کمک به زنده ماندن بیمار است. تحقیقات مختلفی، (به عنوان مثال [1، 2]) ارائه شده Toregas و همکاران (1974)، در مورد مسائل مربوط به مکان یابی آمبولانس انجام شده است.
6. نتیجه گیری
این مقاله یک مشکل مکان یابی آمبولانس با مجموعه ای از ابهام در تقاضا را مورد بررسی قرار می دهد که در آن توزیع احتمال تقاضای نامشخص، مجهول است. در این محیط داده محور، تنها تقاضاهای میانگین و کوواریانس در نقاط اضطراری شناخته شده اند. مشکل، تعیین موقعیت پایگاه ها و تعداد آمبولانس ها در هر پایگاه، با هدف به حداقل رساندن هزینه کل مرتبط با مکان یابی پایگاه ها و اختصاص دادن آمبولانس ها است. ما یک مدل آزاد توزیع با محدودیت های احتمالی پیشنهاد می کنیم. سپس دو فرمول MIP تقریبی با روش های تقریب مختلف محدودیت های شانسی پیشنهاد شده است که مبتنی بر مجموعه ابهام های توزیع احتمال ناشناخته هستند. آزمایش های عددی بر روی معیارها و 120 نمونه ایجاد شده به صورت تصادفی انجام شده و نتایج محاسباتی نشان می دهد که اولین فرمول MIP تقریبی با هزینه بالای سیستم بسیار محافظه کارانه تر است، در حالی که فرمول MIP تقریبی دوم صرفه جویی در هزینه بیشتر با سطح خدمات مناسب را تضمین می کند.
Ambulance location problem is a key issue in Emergency Medical Service (EMS) system, which is to determine where to locate ambulances such that the emergency calls can be responded efciently. Most related researches focus on deterministic problems or assume that the probability distribution of demand can be estimated. In practice, however, it is difcult to obtain perfect information on probability distribution. Tis paper investigates the ambulance location problem with partial demand information; i.e., only the mean and covariance matrix of the demands are known. Te problem consists of determining base locations and the employment of ambulances, to minimize the total cost. A new distribution-free chance constrained model is proposed. Ten two approximated mixed integer programming (MIP) formulations are developed to solve it. Finally, numerical experiments on benchmarks (Nickel et al., 2016) and 120 randomly generated instances are conducted, and computational results show that our proposed two formulations can ensure a high service level in a short time. Specifcally, the second formulation takes less cost while guaranteeing an appropriate service level.
1. Introduction
Te design of Emergency Medical Service (EMS) systems that afects people’s health and life focuses on how to respond to emergencies rapidly. Ambulance location problem is one of the key problems in EMS system, which mainly consists of determining where to locate bases, also named as emergency service facilities, and the employment of ambulances in order to serve emergencies efciently and to guarantee patient survivability. Tere have been various researches investigating ambulance location problem (e.g., [1, 2]) since it is introduced by Toregas et al. (1974).
6. Conclusion
Tis paper investigates an ambulance location problem with ambiguity set of demand, in which the probability distribution of the uncertain demand is unknown. In such a datadriven environment, only the mean and covariance demands at emergency points are known. Te problem is to determine the base locations and the number of ambulances at each base, aiming at minimizing the total cost associated with locating bases and assigning ambulances. We propose a distribution-free model with chance constraints. Ten two approximated MIP formulations with diferent approximation methods of chance constraints are proposed, which are based on diferent ambiguity sets of the unknown probability distribution. Numerical experiments on benchmarks and 120 randomly generated instances are conducted, and the computational results show that the frst approximated MIP formulation is much conservative with overhigh system cost, while the second approximated MIP formulation is more cost saving with service level appropriately ensured.
1. مقدمه
2. بررسی ادبیات
2.1 مشکل مکان یابی آمبولانس با تقاضای مبهم
2.2 روش های آزاد توزیع
3. شرح و فرمول بندی مشکل
3.1 شرح مشکل
3.2 ساخت محدودیت شانسی
3.3. فرمولاسيون آزاد توزيع
4. رویکردهای راه حل
4.1 فرمول تقریبی MIP MIP-DF1:
4.2 فرمول تقریبی MIP: MIP-DF2
5. آزمایشات محاسباتی
5.1 آزمایش خارج از نمونه
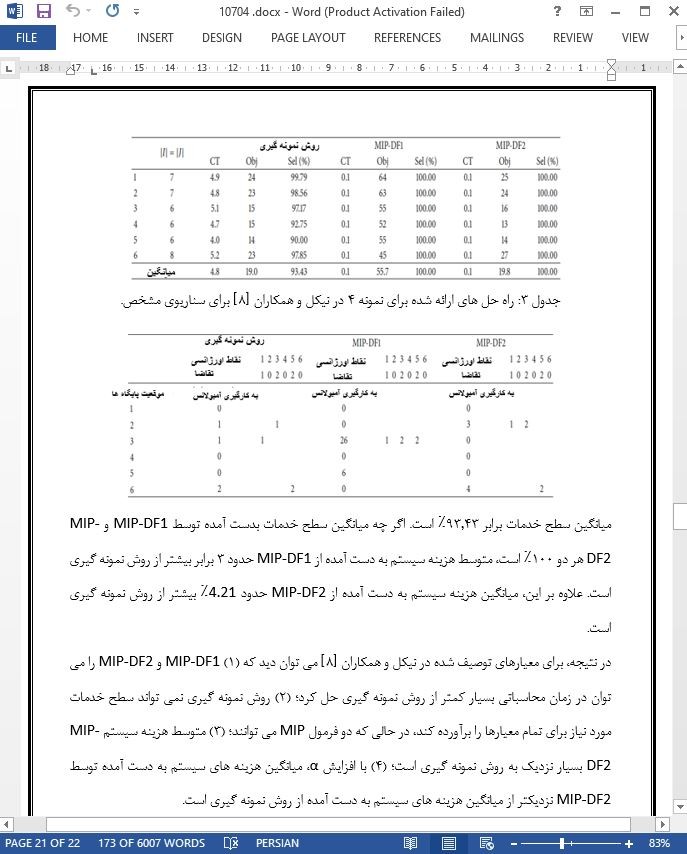
5.2 نمونه های معیار
5.3 آزمایش های محاسباتی بر روی نمونه های ایجاد شده به صورت تصادفی
6. نتیجه گیری
1. Introduction
2. Literature Review
2.1. Ambulance Location Problem with Uncertain Demand
2.2. Distribution-Free Approaches
3. Problem Description and Formulation
3.1. Problem Description
3.2. Chance Constraint Construction
3.3. Distribution-Free Formulation
4. Solution Approaches
4.1. Approximated MIP Formulation
4.2. Approximated MIP Formulation
5. Computational Experiments
5.1. Out-of-Sample Test
5.2. Benchmark Instances
5.3. Computational Tests on Randomly Generated Instances
6. Conclusion
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه
