
الگوریتم کنترل توزیع شده برای کنترل بهینه توان راکتیو در شبکه های قدرت
چکیده
تولید توان راکتیو همواره برای حداقل کردن تلفات توان و بهبود پروفایل ولتاژ در سیستمهای قدرت استفاده شده است. به هرحال، به دلیل اینکه تولید توان راکتیو تا حدی بر قابلیت کنترل فرکانس ژنراتور تاثیر میگذارد، هزینههای مربوط به آن باید درنظر گرفته شود. این مقاله یک روش کنترل غیرخطی مبتنی بر الگوریتم را پیشنهاد میدهد، تا به تولید توان راکتیو بهینه برای چندین ژنراتور در شبکه قدرت دست پیدا کند. هر ژنراتور برای به روز رسانی تنظیمات کنترل توان راکتیو خود تنها به اندازهگیرههای محلی و تبادل اطلاعات با باسهای مجاور خود نیاز دارد. در این مقاله نشان داده شده است که الگوریتم ارائه شده میتواند بطور یکنواخت از حالت غیرمحدب بودن تابع هدف بکاهد تا همگرا شود و با سرعت همگرایی بیشتر به جوابهای قابل قبول در مقایسه با تکنیک متمرکز PSO (بهینهسازی ازدحام ذرات) دست یابد. الگوریتم ارائه شده روی شبکه 9 باس، 39 باس و 162 باس IEEE پیادهسازی شده است تا کارایی و مقیاسپذیری آن بررسی شود.
مقدمه
تولید توان راکتیو به طور گسترده بمنظور بهبود ولتاژ باسها، همچنین حداقل نمودن تلفات توان در سیستمهای قدرت سنتی استفاده شده است. تکنیکهای بهینهسازی و کنترل بسیاری برای کنترل بهینه توان راکتیو مانند، برنامهریزی خطی، روش گرادیان، روش جستجوی نقطه میانی و الگوریتم برنامه ریزی مجذوری متوالی معرفی شدهاند. از نقطه ضعف این راهحلها میتوان حساسیت به شرایط اولیه و محدودیتهای ریاضی بر تابع هدفها مانند محدب بودن آنها را نام برد. اخیرا، ایدههای محاسباتی زیادی بصورت یک روش ارائه شدهاند تا بر عیبهای الگوریتمهای سنتی مانند، الگوریتم جستجوی گرانشی، الگوریتم تکاملی تفاضلی، الگوریتم ژنتیک پیشرفته، کلونی زنبور عسل مصنوعی، و بهینهسازی ازدحام ذرات (PSO) غلبه کنند. به هرحال، همه این الگوریتمها به یک شبکه ارتباطی پیشرفته برای جمعآوری اطلاعات سراسری نیاز دارند و همواره بصورت آفلاین در یک روش متمرکز میباشند.
نتیجهگیری
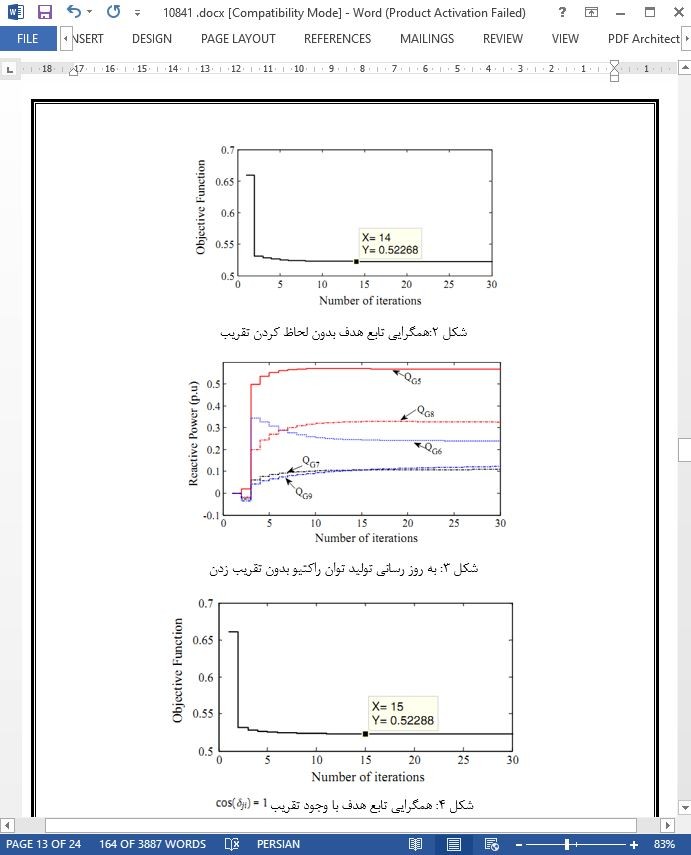
این مقاله یک الگوریتم کنترل غیر خطی توزیع شده برای کنترل بهینه توان راکتیو چندین ژنراتور در یک شبکه قدرت پیشنهاد کرد. تلفات توان اکتیو، انحراف ولتاژ و هزینه تولید توان راکتیو در تابع هدف منظور شدند و کنترل بهینه تولید توان راکتیو چندین ژنراتور بصورت یک مسئله غیر-محدب فرمولسازی شد. تنها از اطلاعات مبادله شده بین باسهای مجاور استفاده میشود تا جواب بهینه بدست آید، بنابراین در مقایسه با الگوریتمهای متمرکز بار محاسباتی و ارتباطی این الگوریتم کمتر خواهد بود. همچنین این موضوع اثبات شد که با در نظر گرفتن تقریب cos(δji) = 1 در حالت سطح بار/تولید معمولی، در مقایسه با حالتی که از این تقریب استفاده نشود، میتوان به نتایج قابل قبولی دست یافت و الگوریتم را برای کاربردهای آنلاین ساده نمود. کارایی الگوریتم کنترل غیرخطی توزیع شده معرفی شده در شبکههای 9، 39 و 162 باس IEEE مورد بررسی قرار گرفت و نتایج شبیهسازی با استفاده از این الگوریتم و با استفاده الگوریتم متمرکز PSO مورد مقایسه قرار گرفتند.
Abstract
Reactive power generation has been commonly used for power loss minimization and voltage profile improvement in power systems. However, the opportunity cost of reactive power generation should be considered since it affects the frequency control capability of the generator to some degree. This paper proposed a distributed nonlinear control based algorithm to achieve the optimal reactive power generation for multiple generators in a power grid. The reactive power control setting update for each generator only requires local measurement and information exchange with its neighboring buses. It is demonstrated that the proposed algorithm can reduce the non-convex objective function monotonically till convergence and achieve comparable solutions to the centralized technique: particle swarm optimization with faster convergence speed. The proposed algorithm has been tested on the IEEE 9-bus, 39-bus and 162-bus systems to validate its effectiveness and scalability.
Introduction
Reactive power generation has been widely used to improve the voltage of the buses as well as minimize the power loss in the conventional power systems. Abundant control and optimization techniques have been developed for the optimal reactive power control such as linear programming [1], gradient method [2], interior point method [3,4], and sequential quadratic programming algorithm [5]. Shortcomings of these solutions include sensitivity to initial conditions and mathematical restriction on objective functions, such as convexity. Recently, numerous computational intelligent based methods have been proposed to overcome the shortcomings of the traditional algorithms such as, Gravitational Search Algorithm [6], Differential Evolution Algorithm [7], Enhanced Genetic Algorithm [8], Artificial Bee Colony [9], and Particle Swarm Optimization (PSO) [10]. However, all these algorithms require sophisticated communication network for global information collection and are usually implemented offline in a centralized way.
Conclusions
This paper proposed a distributed nonlinear control based algorithm for optimal reactive power control of multiple generators in a power grid. Active power loss, voltage deviation and reactive power generation cost are taken into consideration, and the optimal reactive power control of multiple generators is formulized as a non-convex problem. Only information exchange among neighboring buses is used to achieve the optimal solution, thus, the computational and communication burden are reduced compared to centralized algorithms. It has been demonstrated that by approximating cos(dji) = 1, the calculation for online application is simplified and can still provide comparable results to that of the one without approximation at normal level of generation/load condition. The effectiveness of the proposed distributed nonlinear control based algorithm is validated by comparing to the centralized algorithm: PSO, for IEEE 9-bus, 39-bus and 162-bus systems.
چکیده
مقدمه
فرمولسازی مسئله
طراحی الگوریتم معرفی شده
کنترل غیرخطی توزیع شده برپایه الگوریتم
اجرای الگوریتم پیشنهاد شده
مطالعات شبیهسازی
مورد مطالعه 1: سیستم 9 باس
آنالیز تاثیر سطح تولید/مصرف بالا و ضرایب وزنی مختلف
مورد مطالعاتی 2: سیستم 39 باس
مورد مطالعاتی 3: سیستم 162 باس
نتیجهگیری
Abstract
Introduction
Problem formulation
Proposed algorithm design
Distributed nonlinear control based algorithm
Implementation of the proposed algorithm
Simulation studies
Case study 1: 9-bus system
High level of generation/load and different weight coefficients influence analysis
Case study 2: 39-bus system
Case study 3: 162-bus system
Conclusions
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه
