مدل ریسک متوسط برای انتخاب پورتفولیوی غیرقطعی با ریسک پس زمینه
چکیده
در زمان اتخاذ تصمیمات سرمایه گذاری، نه تنها با ریسک داراییهای مالی در پورتفولیو، بلکه با ریسک پس زمینه نیز مواجه می شویم. در این مقاله، یک مسئله انتخاب پورتفولیوی غیرقطعی مورد بحث قرار میگیرد که در آن ریسک پسزمینه در نظر گرفته میشود و بازده اوراق بهادار و داراییهای پسزمینه به جای ارقام و اطلاعات تاریخی توسط ارزیابی کارشناسان مجرب ارائه میشود. با در نظر گرفتن بازده اوراق بهادار و دارایهای پس زمینه به عنوان متغیرهای غیرقطعی، ما یک مدل ریسک متوسط غیرقطعی را با ریسک پس زمینه برای انتخاب پورتفولیو مطرح می کنیم و شکلهای قطعی این مدل را در زمانی که بازده اوراق بهادار و بازده دارایی پسزمینه از توزیع نرمال عدم قطعیت پیروی می کند ارائه می دهیم. نتیجه گرفته میشود که وقتی همه چیز یکسان باشد، بازده پرتفولیوی بهینه مورد انتظار با ریسک پسزمینه بطور معمول کمتر از زمانی است که ریسک پسزمینه وجود نداشته باشد. علاوه براین، ما در مورد رابطه بین راه حل بهینه مدل خود و مدل ارائه شده در مقاله Huang تحت عنوان " انتخاب پروتفولیوی غیرقطعی با ریسک پس زمینه" بحث می کنیم. در نهایت، مثالهای عددی را ارائه می دهیم تا کارایی مدل و همچنین تاثیر ریسک پس زمینه را بر تصمیم سرمایه گذاری نشان دهیم.
1. مقدمه
مسئله انتخاب پروتفولیو این است که چگونه در اوراق بهادار پرمخاطره سرمایه گذاری کنیم تا بازده پورتفولیو را با کنترل ریسک به حداکثر برسانیم. Markowitz (1) ابتدا در سال 1952 مدل واریانس متوسط را که اساس نظریه پورتفولیوی مدرن است و بیشترین تاثیر را در توسعه مدیریت مالی ریاضی داشته است، مطرح کرد. با این حال، ارزیابی ریسک با واریانس بازده یک پورتفولیو دارای محدودیت هایی است. با توجه به این امر، محققان روشهای دیگری را برای اندازه گیری سرمایه گذاری در نمونه کارها مورد مطالعه قرار دادند و مدل های زیادی از بهینه سازی پورتفولیو را ارائه دادند که عبارتند از مدل نیمه واریانس متوسط (2،3) ، مدل انحراف مطلق (4)، مدل ارزش در معرض خطر (5،6)، مدلهای شرطی ارزش در معرض خطر (7،8)، مدل CVaR نیمه واریانس متوسط (9) و غیره. در این مقاله، منحنی ریسک (10) به عنوان معیار ریسک مورد استفاده قرار می گیرد، زیرا آن اطلاعاتی را در مورد همه زیانهای احتمالی فراهم می آورد.
4. نتیجه گیری
در این مقاله، تاثیر ریسک پس زمینه بر سرمایه گذاریها مورد بحث قرار گرفته است. در یک محیط پیچیده مالی و اجتماعی، موقعیتهایی وجود دارد که در آن بازده داراییهای پس زمینه و بازده اوراق بهادار باید توسط کارشناسان مجرب با توجه به عوامل غیرمنتظره و کمبود داده ها و اطلاعات تاریخی مورد ارزیابی قرار گیرند. این مقاله در این خصوص بحث می کند که سطح ریسک می تواند با منحنی ریسک و مدل ریسک متوسط غیرقطعی با ریسک پس زمینه برای انتخاب پورتفولیو ارزیابی شود. معادلهای قطعی این مدل ارائه شده اند. علاوه براین، برای هر rتعیین شده، مشاهده کردیم که بازده مورد انتظار پورتفولیوی بهینه با ریسک پس زمینه کوچکتر از حالت بدون ریسک آن است. مدل ما که با مدل Huang متفاوت است، می تواند همه ریسکهای ممکنی را که سرمایه گذاران می توانند تحمل کنند مورد نظر قرار دهد.
در پایان، مثالهای عددی و همچنین تجزیه و تحلیلها نشان می دهند که مدل ریسک متوسط با ریسک پس زمینه می تواند مدل موثری باشد و ریسک پس زمینه دارای تاثیر زیادی بر تصمیم سرمایه گذاری است.
Abstract
When making investment decisions, one will face not only the risk of financial assets within portfolio but also background risk. This paper discusses an uncertain portfolio selection problem in which background risk is considered and the security returns and background assets return are given by experienced experts’ evaluations instead of historical data. Regarding the returns of the securities and background assets as uncertain variables, we propose an uncertain mean-risk model with background risk for portfolio selection and the crisp forms of the model are provided when security returns obey different uncertainty distributions. In addition, when everything else is same, it is concluded that the optimal expected return of the mean-risk model with background risk is usually smaller than that without background risk. Moreover, the relationship between the optimal solution of our model and that of the model in Huang’s paper “Uncertain Portfolio Selection with Background Risk” is discussed. Finally, numerical examples are presented to illustrate the effectiveness of the model and to show the effect of background risk on investment decision.
1. Introduction
Portfolio selection problem is to consider how to allocate one’s capital in different risky securities in order to maximize the return of portfolio with risk control. Markowitz [1] first proposed the mean–variance model in 1952, which is the foundation of modern portfolio theory and has been the most impact-making development in mathematical finance management. However, measuring the risk by the variance of return of a portfolio has some limitations. In view of this, scholars studied other methods to measure investment risk of the portfolio and built a lot of portfolio optimization models, such as, mean– semivariance model [2,3], expected absolute deviation model [4], Value-at-Risk model [5,6], Conditional Value-at-Risk models [7,8], mean–semivariance–CVaR model [9], etc. In this paper, risk curve [10] will be used as the risk measure since it provides information about all the likely losses.
4. Conclusions
In this paper, the effect of the background risk on investments has been discussed. In the complex financial and social environment, there are situations where background assets return and the security returns have to be evaluated by experienced experts due to the unexpected things and the lack of historical data. This paper has discussed that risk level can be measured by risk curve and proposed uncertain mean-risk model with background risk for portfolio selection. The crisp equivalents of the model are provided. In addition, for any given r, we have found that the expected return of the optimal portfolio with background risk is smaller than that without background risk. Different from Huang’s model, our model can consider all the possible risks that investors could tolerate.
Finally, both the numerical examples and the analysis show that the mean-risk model with background risk is effective and background risk has a great effect on the investment decision.
چکیده
1. مقدمه
2. مدلهای ریسک متوسط با ریسک پس زمینه
2.1. مدلهای غیرقطعی
2.2. شکل قطعی مدل ریسک متوسط با ریسک پس زمینه
2.3. بحث در مورد راه حل بهینه مدل ریسک متوسط با ریسک پس زمینه
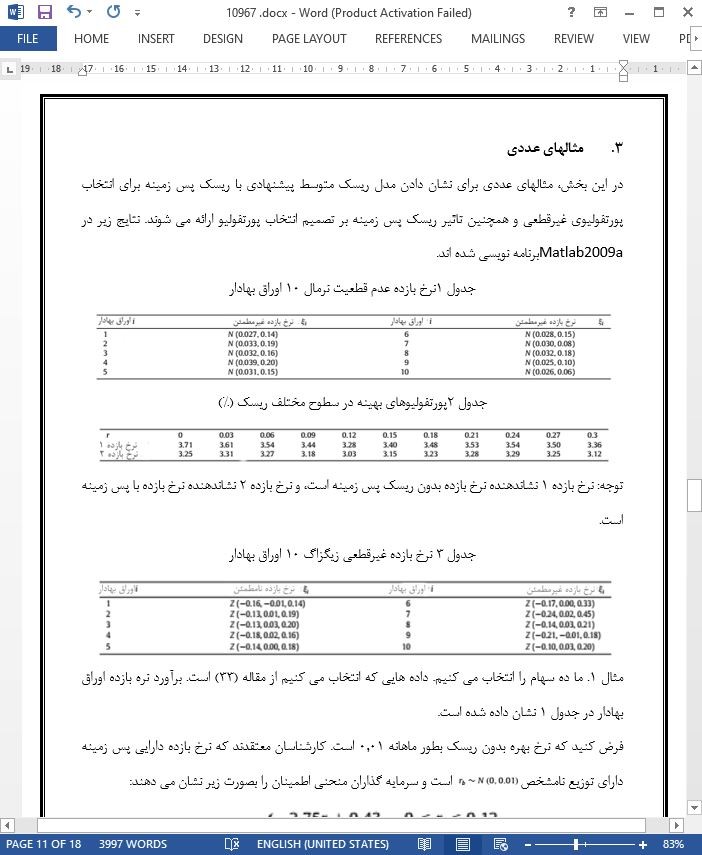
3. مثالهای عددی
4. نتیجه گیری
Abstract
1. Introduction
2. Mean-risk models with background risk
2.1. Uncertain models
2.2. Crisp form of mean-risk model with background risk
2.3. Discussion of the optimal solution of the mean-risk model with background risk
3. Numerical examples
4. Conclusions
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه