تير اويلر-برنولی سه بعدی غيرخطی ارتقا يافته با پایه متحرک
چکیده
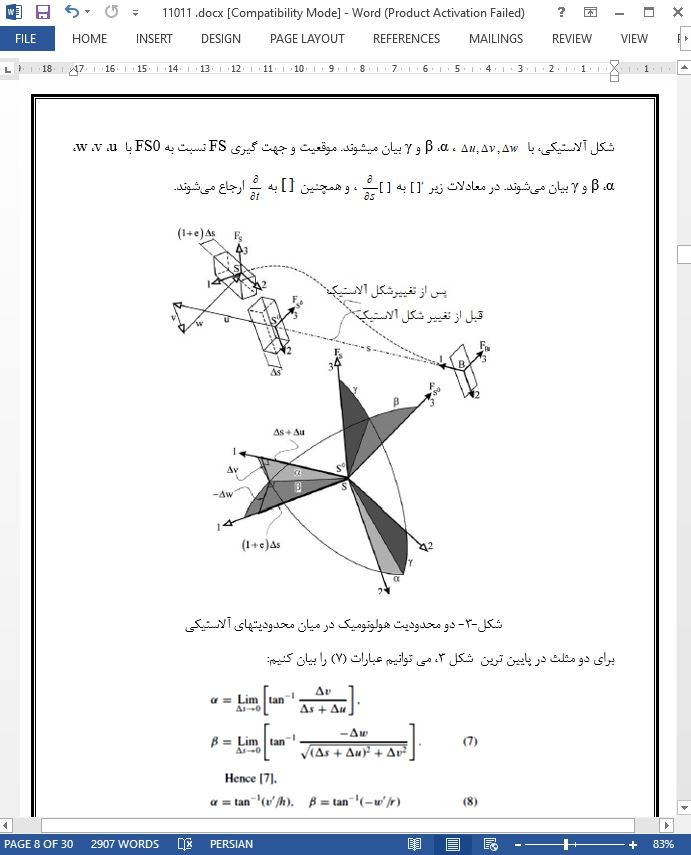
معادلات دیفرانسیل حرکت با مشتقات جزئی ، با استفاده از اصل همیلتون در تیر متحرک اویلر - برنولی سه بعدی حاصل میشود. تنش بصورت سه بعدی و با چشمپوشی از تابیدگی درون صفحه ای و برون صفحه ای سطح مقطع رفتار میکند. کشش، فشار،پیچش، خیزهای فضایی، با یکدیگر کوپلشدگی غیرخطی دارند. پایه متحرک تیر دارای سه درجه آزادی انتقالی و سه درجه آزادی دورانی است. تیر از ماده ارتجاعی ایزوتروپیک به صورت خطی ساخته شده است و به صورت دینامیکی دقیق تر از تیر اویلر- برنولی مدل شده است. دقت در تئوری اویلر برنولی غیرخطی سه بعدی معمولی، ناشی از دو ترم آلاستیکی جدید است که با دیفرانسیل گیری از میدان تقریب کرنشی مربوط به گرایش آلاستیکی ناچیز از قاب مقطع عرضی، در این تئوری آشکار نشده بود. در این مقاله، از میدان کرنشی دقیق مربوط به گرایش آلاستیکی قابل توجه در قاب عرضی به عنوان منبع مشتقگیری استفاده میکنیم، گرچه از گرایش آلاستیکی سطح مقطع چشم پوشی میشود.
مقدمه
تیرها یکی از مهمترین المانهای سازه در زمینههای مهندسی هستند. طراح تیرهای انعطافپذیر را برای ارائه سازه با وزن کم انتخاب میکند. هرچقدر انعطافپذیری تیرها افزایش پیدا کند، درمقابل مدلسازی دینامیکی پیچیدهتر میشود.
کارای وهمکارانش ، در زمینه دو لینک انعطاف پذیر فضایی، مبتنی بر بازوی مکانیکی انعطاف پذیر به صورت تیرهای اویلر برنولی بحث کردند که آزادانه و به صورت مقطعی در صفحه مداری تغییر شکل داده میشوند. هیلر تنها سه درجه آزادی آلاستیک را برای هر لینک، بصورت تیر اویلر برنولی درنظر گرفت. شی و همکارانش ]3[، لینک انعطاف پذیر دو وجهی را با تیر اویلر- برنولی مدل کردند. چن [4] یک مدل دینامیکی خطی، برای بازوهای مکانیکی انعطاف پذیر چند لینکه و دو وجهی ارائه داده اند که شامل تعدادی لینک انعطاف پذیری اختیاری بود.
9- نتیجهگیری
معادلات دیفرانسیل حرکت غیرخطی با مشتقات جزئی تیر اویلر – برنولی 3 بعدی با پایه متحرک شش درجه آزادی بیان شد. فشار- کشش ، پیچش و دو خمش فضایی تیر آزمایش شد، درهنگامی که گرایش آلاستیکی ناچیزی در قاب سطح مقطع آن تولید می شود. معادلات حرکتی شامل دو اصطلاح آلاستیکی جدید است که در تئوری تیر اویلر – برنولی سه بعدی غیر خطی معمولی با مشتق گیری از میدان کرنش تقریبی مربوط به گرایش آلاستیک ناچیز در قاب سطح مقطع ظاهر نشده بود. دیفرانسیلگیری باید از میدان کرنش دقیق مربوط به گرایش آلاستیک بزرگ در قاب سطح مقطع بدست آید. این دو اصطلاح آلاستیکی جدید معادلات حرکتی دقیقتری نسبت به تئوری تیر اویلر –برنولی سه بعدی غیر خطی نتیجه میدهند. آنها برای تئوری تیر اویلر – برنولی سه بعدی خطی ارتقا یافته در نظر گرفته میشوند.
Abstract
Using Hamilton’s principle the coupled nonlinear partial differential motion equations of a flying 3D Euler–Bernoulli beam are derived. Stress is treated three dimensionally regardless of in-plane and out-ofplane warpings of cross-section. Tension, compression, twisting, and spatial deflections are nonlinearly coupled to each other. The flying support of the beam has three translational and three rotational degrees of freedom. The beam is made of a linearly elastic isotropic material and is dynamically modeled much more accurately than a nonlinear 3D Euler–Bernoulli beam. The accuracy is caused by two new elastic terms that are lost in the conventional nonlinear 3D Euler–Bernoulli beam theory by differentiation from the approximated strain field regarding negligible elastic orientation of crosssectional frame. In this paper, the exact strain field concerning considerable elastic orientation of crosssectional frame is used as a source in differentiations although the orientation of cross-section is negligible.
1 Introduction
Beams are one of the most important structural elements in engineering fields. To provide the structure with less weight makes designer choose more flexible beams. As the flexibility of the beam increases, its dynamic modeling becomes more complicated in return.
Karray et al. [1] have treated the two flexible links of space-based flexible manipulator as Euler–Bernoulli beams, free to deform transversely in the orbital plane. Hiller [2] has considered only three elastic degrees of freedom for each link as an Euler–Bernoulli beam. Shi et al. [3] have modeled a planar flexible link by an Euler–Bernoulli beam. Chen [4] has presented a linearized dynamic model for multilink planar flexible manipulators which can include an arbitrary number of flexible links. 9
Conclusions
Nonlinear partial differential equations of motion of a 3D Euler–Bernoulli beam with six-DOF flying support are exposed. The beam experiences compression, tension, torsion, and two spatial bendings elastically while negligible elastic orientation is produced in its crosssectional frame. The motion equations involve two new elastic terms that had been lost in the traditional nonlinear 3D Euler–Bernoulli beam theory by differentiation from the approximated strain field regarding negligible elastic orientation of cross-sectional frame. The differentiation should have been derived from the exact strain field concerning large elastic orientation of the crosssectional frame. These two elastic terms have given the resulting motion equations a higher accuracy than that of the nonlinear 3D Euler–Bernoulli beam theory. They account for the enhancement of the nonlinear 3D Euler–Bernoulli beam theory.
چکیده
1- مقدمه
2- پایه متحرک تیر
3-تیر
1-3- محدودیتهای سازه تیر
4- تغییرات انرژی جنبشی
5- تغییرات انرژی پتانسیل گرانشی
6- تغییرات انرژی پتانسیل آلاستیک
7- معادلات حرکت
8- بررسی وتایید معادلات حرکت
1-8- مورد I: جسم صلب متحرک تحت نیروی گرانشی
2-8- تیرکوتاه اویلر- برنولی سه بعدی غیرخطی ارتقا یافته
3-8- مورد III: تیر کوتاه اویلر – برنولی سه بعدی غیر خطی با پایه ثابت
9- نتیجهگیری
Abstract
1 Introduction
2 Flying support of the beam
3 Beam
3.1 Beam structural constraints
4 Variation of kinetic energy
5 Variation of gravitational potential energy
6 Variation of elastic potential energy
7 Motion equations
8 Verification of the motion equations
8.1 8.1 Case I: Flying rigid body under gravitational force
8.2 Case II: Enhanced nonlinear 3D short Euler–Bernoulli beam with a fixed support
9 Conclusions
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه