بهینه سازی استوار نسبت CVaR STARR مختلط با استفاده از مفصل ها
چکیده
ما مدلهای بهینه سازی استوار برای دو نوع نسبت بازده تنظیم شده با دنباله ثابت (STARR)، یکی با ارزش در ریسک شرطی ترکیبی (MCVaR) و دیگری با ارزش در ریسک ترکیبی انحرافی (DMCVaR)، با ابهام مشترک در توزیع مدلسازی شده با استفاده از مفصل ها، معرفی می کنیم. این دو مدل نشان داده می شوند تا برنامه های خطی از نظر محاسباتی، قابل ردیابی باشند. از یک روش دو مرحله ای برای بکارگیری ساختار وابستگی مشترک در میان دارایی ها استفاده می کنیم. در ابتدا، باقیمانده فیلتر شده از مجموعه های بازده هر دارایی را با استفاده از میانگین متحرک خودبازگشتی مدل تعمیم یافته واریانس ناهمگن شرطی خودبازگشتی گلاستن ، جاگاناتان و رانکل (ARMA-GJR-GARCH) استخراج می کنیم. در ادامه، از مفصل های واین با قاعده برای مدلسازی همبستگی اشتراکی بین باقیمانده های تبدیل شده استفاده می کنیم. ساختار درختی در واین های با قاعده با استفاده از تاو کندال انجام می شوند. ما عملکرد دو مدل استوار پیشنهادی را با مشابهت های معمولی بین آنها، که تنها با استفاده از مفصل گاوسی بیان می شود، هنگام توزیع مشترک در دومی مقایسه می کنیم. همچنین، عملکرد سبد سهام بدست آمده را در مقابل سبد سهام بدست آمده از مدل مارکوییتز و مدلهای GARCH چند متغیره، با استفاده از تحلیل پنجره نَوَرد بررسی می کنیم. ما عملکرد بالاتر مدلهای استوار پیش بینی شده را نسبت به مدلهای مشابه معمولی در بازده های میانگین اضافی، نسبت سورتینو ، نسبت راچِو ، نسبت VaR، و نسبت ترینر ، در سه مجموعه داده شامل شاخص های کلی نشان می دهیم.
1. مقدمه
از آغاز دوره نظریه جدید سبد سهام با تحقیق اولیه مارکوییتز [53]، که معیار ریسک سرمایه گذاری را به صورت انحراف استاندارد توزیع بازدهی در نظر گرفت، شاهد گسترش چندین مدل بهینه سازی پاداش-ریسک در متون تحقیقاتی بوده ایم. این مدل ها، هدف مشترکی برای یافتن یک سبد سهام بهینه با حداکثربازده و حداقل ریسک دارند. به طور کلی، مدلهای دو منظوره به مسائل یک منظوره با حداکثر بازده با توجه به حد بالای ریسک و حداقل ریسک باتوجه به حد پایین بازده یا حداکثرسازی تابع سود بازده-ریسکِ ترکیبی با یک پارامتر مشخص ریسک گریزی، تبدیل می شوند.راه حل های بهینه مسائل نتیجه شده، به ترتیب نسبت به انتخاب حد بالا، حد پایین، و پارامتر ریسک گریزی، حساس هستند.
7. نتایج
بازده سبد سهام، یک متغیر تصادفی چند متغیره است که توزیع ان وابسته به ساختار وابستگی در میان تشکیلات آن است. این وابستگی نیاز به بکارگیری دقیق تصمیمات درست سرمایه گذاری دارد. نظریه مفصل، یک مکانیسم بسیار پذیرفته شده برای بکارگیری ساختار وابستگی با در نظر گرفتن بیشترین ویژگی های روش موجود در داده های مالی، مانند عدم تقارن، دنباله های بزرگ، و غیر خطی بودن می باشد. با این حال، پویایی های همواره در حال تغییر بازار، پیچیده تر می شود تا به اندازه کافی توسط یک تابع مفصل واحد بیان شوند. فرض می کنیم که از مفصل های مختلط، ترکیبی خطی از مفصل های مختلف، استفاده کنیم تا ساختار وابستگی را در بازده های سبد سهام تطبیق دهیم.
Abstract
We introduce the robust optimization models for two variants of stable tail-adjusted return ratio (STARR), one with mixed conditional value-at-risk (MCVaR) and the other with deviation MCVaR (DMCVaR), under joint ambiguity in the distribution modeled using copulas. The two models are shown to be computationally tractable linear programs. We apply a two-step procedure to capture the joint dependence structure among the assets. We first extract the filtered residuals from the return series of each asset using AutoRegressive Moving Average Glosten Jagannathan Runkle Generalized Autoregressive Conditional Heteroscedastic (ARMA-GJR-GARCH) model. Subsequently, we exploit the regular vine copulas to model the joint dependence among the transformed residuals. The tree structure in the regular vines is accomplished using Kendall’s tau. We compare the performance of the proposed two robust models with their conventional counterparts when the joint distribution in the latter is described using Gaussian copula only. We also examine the performance of the obtained portfolios against those from the Markowitz model and multivariate GARCH models using the rolling window analysis. We illustrate the superior performance of the proposed robust models than their conventional counterpart models on excess mean returns, Sortino ratio, Rachev ratio, VaR ratio, and Treynor ratio, on three data sets comprising of indices across the globe.
1. Introduction
Since the beginning of the era of modern portfolio theory with the pioneering work of Markowitz [53], where the measure of risk in investment is taken to be the standard deviation of return distribution, the literature has seen a proliferation of several rewardrisk optimization models. These models have a common aim to find an optimal portfolio of maximum return and minimum risk. The bi-objective models generally are transformed into single objective problems of maximizing return given an upper bound on risk or minimizing risk given a lower bound on the return or maximizing the combined returnrisk utility function for a given risk-aversion parameter. The optimal solutions of the resulting problems are sensitive to the choice of the upper bound, lower bound, and riskaverse parameter, respectively.
7. Conclusions
Portfolio return is a multivariate random variable whose distribution depends on the underline dependence structure among its constitutes. This dependency needs to be capture carefully for correct investment decisions. Copula theory is a widely accepted mechanism to capture the dependency structure by accounting for most stylized features present in the financial data, like asymmetry, fat-tails, and nonlinearity. However, the ever-changing market dynamics is more complicated to be adequately represented by a single copula function. We propose to use mixture copulas, a linear combination of various copulas, to fit the dependence structure in portfolio returns.
چکیده
1. مقدمه
سهم ها
2. مرور ادبیات
2.1. نسبت پاداش-ریسک
2.2. مفصل های واین
2.3. بهینه سازی استوار
3. مدلسازی چند متغیره
3.1. مدل ARMA-GJR-GARCH برای توزیع حاشیه ای
3.2. مفصل ها
3.3. مفصل های واین
4. فرمولاسیون مدل ها
4.1. علائم
4.2. مدل نسبت STARR با CVaR مختلط و CVaR مختلط انحرافی
4.3. مدلهای استوار نسبت STARR
5. متدلوژی و داده ها
5.1. متدلوژی
5.2. داده ها
6. تحلیل تجربی
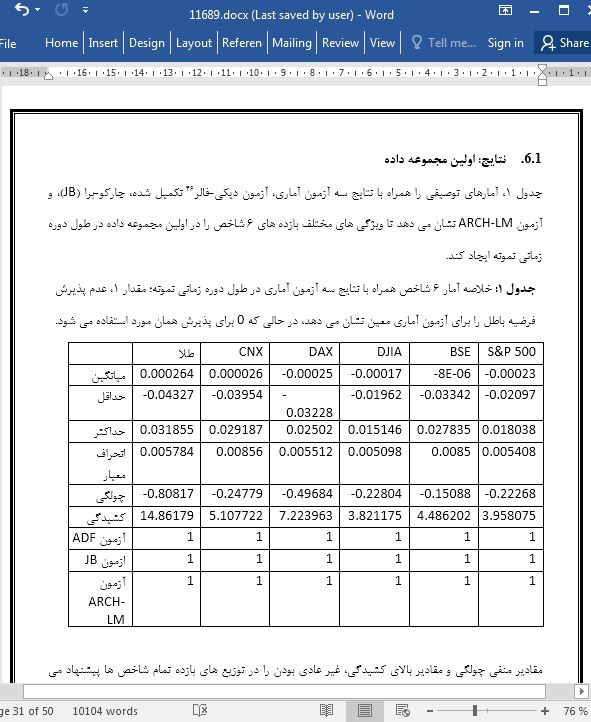
6.1. نتایج: اولین مجموعه داده
6.2. نتایج: دومین مجموعه داده
6.3. سومین مجموعه داده: تحلیل پنجره نورد
7. نتایج
ضمیمه
مفصل های ارشمیدسی
Abstract
1. Introduction
Contributions
2. Literature review
2.1. Reward-Risk Ratio
2.2. Vine Copulas
2.3. Robust Optimization
3. Multivariate modeling
3.1. ARMA-GJR-GARCH model for marginal distribution
3.2. Copulas
3.3. Vine Copulas
4. Models formulation
4.1. Notations
4.2. STARR Ratio Model with Mixed CVaR and Mixed Deviation CVaR
4.3. Robust STARR Ratio Models
5. Methodology and data
5.1. The Methodology
5.2. The Data
6. Empirical analysis
6.1. Results: First Data Set
6.2. Results: Second Data Set
6.3. Third Data Set: Rolling Window Analysis
7. Conclusions
Appendix.
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه