ریسک سیستماتیک زمان متغیر (متغیر با زمان)
چکیده
ما در این مقاله کلاس جدیدی از مدلهای پویای مبتنی بر مفصل را برای توزیعات شرطی بعد بالا (با ابعاد بزرگ) پیشنهاد میکنیم که برآورد ابزارهای سنجش متنوعی از ریسک سیستماتیک را تسهیل میکند. مدلهای پیشنهادی ما از ایده های موفقیت آمیز مقالات مربوط به مدلسازی ماتریس های کوواریانس بعد بالا، و از مطالعات اخیر در مورد مدلهای توزیعات عمومی زمان متغیر استفاده میکنند. استفاده ما از مدلهای مبتنی بر مفصل، برآورد مدل مشترک در مراحل را ممکن می سازد و بار مسئولیت محاسباتی را تا حد زیادی کاهش میدهد. ما برای مطالعه مجموعه ای از گستره های تبادل افول اعتبار روزانه (CDS) در 100 شرکت آمریکایی در دوره 2006 تا 2012 از مدلهای پیشنهادی جدید استفاده میکنیم. ما پی بردیم که با اینکه احتمال خطر برای شرکت های منفرد از زمان بحران مالی 2008-2009 تا حد زیادی کاهش پیدا کرده است اما احتمال توأم خطر (ابزار سنجشی برای ریسک سیستماتیک) اکنون نسبت به دوره قبل از بحران خیلی بالاتر است.
1. مقدمه
ریسک سیستماتیک را بطور کلی میتوانیم بصورت ریسک سختی و مشکلات (خطر) در تعداد زیادی از شرکت ها یا مؤسسات تعریف کنیم. ریسک سیستماتیک نشاندهنده یک رویداد انتهایی در دو مسیر است: یک ضرر بزرگ (بعنوان مثال در تطابق با یک تحقق تعقیبی چپ برای بازده سهام)، در امتداد نسبت (بخش) بزرگی از شرکتها. ریسک سیستماتیک با خطر سیستماتیک تفاوت دارد از این لحاظ که خطر سیستماتیک معمولاً به معنای قرارگیری یک دارائی در معرض یک ریسک عمومی بازار بکار میرود و هیچ ارتباطی با اندازه، جهت و رواج ذاتی در مفهوم «ریسک سیستماتیک» ندارد. روشهای مختلفی برای مطالعه ریسک و وابستگی به مجموعه های کوچک از دارائی ها وجود دارد (برای یک مرور اخیر به پاتون 2013 نگاه کنید) اما روشهای اندکی برای مطالعه وابستگی بین مجموعه بزرگی از دارائی ها موجود است، که این وابستگی برای تحلیل عمومی ریسک سیستماتیک لازم است.
6. نتیجه گیری
ما در مقاله حاضر با توجه رو به رشد در ابزارهای سنجش ریسک رویدادهای سیستماتیک ترغیب شدیم و مدلهای انعطاف پذیر جدید و صرفه جویی را برای توزیعات زمان متغیر بعد بالا (با ابعاد بزرگ) پیشنهاد کردیم. ما از تئوری مفصل استفاده کردیم و مدلهای معروف برای توزیعات تک متغیری را با مدلهای جدید ساختار (مفصل) وابستگی شرطی ترکیب کردیم تا توزیعات توأم پویا را بدست آوریم. ما میتوانیم مدلهای مفصل پویای جدید خود را در ابعاد 100 یا بیشتر اعمال کنیم، که این در مقایسه با ابعاد رایج در مقالات موجود خیلی بزرگتر است. این مدلها از ایده های موفقیت آمیز از مقالات مربوط به مدلسازی پویای ماتریس های همبستگی بعد بالا (بعنوان مثال اینگل 2002) و مطالعات اخیر در مورد مدلهایی برای توزیعات عمومی زمان متغیر (کریل و همکارانش 2013) استفاده میکنند. ما یک برآوردگر از نوع «هدفیابی واریانس» را برای این کلاس از مفصل های پویا پیشنهاد کرده ایم تا تعداد پارامترهایی که توسط بهینه سازی عددی برآورد میشود تا حد زیادی کاهش یابد.
Abstract
This paper proposes a new class of copula-based dynamic models for high-dimensional conditional distributions, facilitating the estimation of a wide variety of measures of systemic risk. Our proposed models draw on successful ideas from the literature on modeling high-dimensional covariance matrices and on recent work on models for general time-varying distributions. Our use of copula-based models enables the estimation of the joint model in stages, greatly reducing the computational burden. We use the proposed new models to study a collection of daily credit default swap (CDS) spreads on 100 U.S. firms over the period 2006 to 2012. We find that while the probability of distress for individual firms has greatly reduced since the financial crisis of 2008-09, the joint probability of distress (a measure of systemic risk) is substantially higher now than in the pre-crisis period.
1 Introduction
Systemic risk can be broadly defined as the risk of distress in a large number of firms or institutions. It represents an extreme event in two directions: a large loss (e.g., corresponding to a large left-tail realization for stock returns), across a large proportion of the firms. It differs from “systematic” risk in that the latter is usually taken to refer to the exposure of an asset to a general market risk, and carries no reference to the size, direction, and prevalence that is inherent in a notion of “systemic” risk. There are a variety of methods for studying risk and dependence for small collections of assets (see Patton (2013) for a recent review) but a paucity of methods for studying dependence between a large collection of assets, which is required for a general analysis of systemic risk.
6 Conclusion
Motivated by the growing interest in measures of the risk of systemic events, this paper proposes new flexible yet parsimonious models for time-varying high-dimensional distributions. We use copula theory to combine well-known models for univariate distributions with new models of the conditional dependence structure (copula) to obtain dynamic joint distributions. Our proposed new dynamic copula models can be applied in dimensions of 100 or more, which is much greater than commonly considered in the literature. These models draw on successful ideas from the literature on dynamic modeling of high-dimensional correlation matrices, (e.g., Engle (2002)) and on recent work on models for general time-varying distributions (Creal, et al. (2013)). We propose a “variance targeting” type estimator for this class of dynamic copulas to dramatically reduce the number of parameters to be estimated by numerical optimization.
چکیده
1. مقدمه
2. یک مدل مفصل پویا برای ابعاد بالا
2.1 مفصل های عاملی
2.2 پویایی امتیاز اتورگرسیو تعمیم یافته
2.3 مفصل های عاملی بعد بالا با پویایی امتیاز اتورگرسیو تعمیم یافته
2.4 وابستگی برابر در مقابل وابستگی ناهمگن
2.5 مدلهای دیگر برای مفصل های پویای بعد بالا
3. مطالعه شبیه سازی
4. توصیف داده و نتایج برآورد
4.1 گستره های تبادل افول اعتبار
4.2 آمار خلاصه
4.3 میانگین شرطی و مدلهای واریانس
4.4 انفجار بزرگ تبادل افول اعتبار
4.5 مقایسه مدلها برای مفصل شرطی
5. ریسک سیستماتیک زمان متغیر
5.1 احتمال توأم آشفتگی
6. نتیجه گیری
ضمیمه: اثبات گزاره 1
Abstract
1 Introduction
2 A dynamic copula model for high dimensions
2.1 Factor copulas
2.2 Generalized autoregressive score dynamics
2.3 High-dimensional factor copulas with GAS dynamics
2.4 Equidependence vs. heterogeneous dependence
2.5 Other models for dynamic, high-dimensional copulas
3 Simulation study
4 Data description and estimation results
4.1 CDS spreads
4.2 Summary statistics
4.3 Conditional mean and variance models
4.4 The CDS “Big Bang”
4.5 Comparing models for the conditional copula
5 Time-varying systemic risk
5.1 Joint probability of distress
5.2 Expected proportion in distress
6 Conclusion
Appendix: Proof of Proposition 1
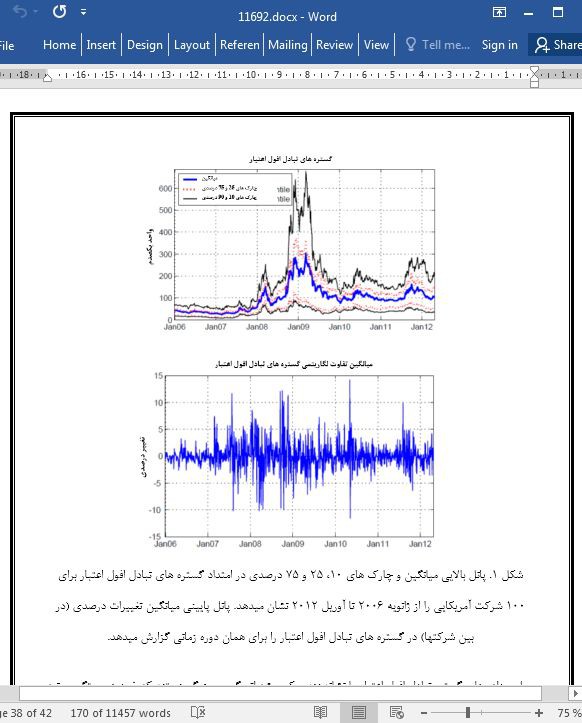
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه