فرآیند تحلیل فازی سلسله مراتبی: تحلیل عملکرد الگوریتم های مختلف
چکیده
فرایند تحلیل سلسله مراتبی( AHP) همراه با نظریه مجموعه فازی ، بطور گسترده در فرایند های تصمیم گیری چند معیاره (MCDM) استفاده شده اند ،که در این فرایند ها اعداد فازی بکارگرفته می شوند تا نشان دهند که قضاوت انسان واقع گرایانه می باشد. در چند دهه ی اخیر مقالات زیادی منتشر شده اند که الگوریتم هایی را با بردار ارجحیت (یا بردار وزنی ) ارائه می دهند که می توانند از طریق ماتریس مقایسه ای فازی محاسبه شوند. هدف این مقاله ، انجام تجزیه و تحلیل عملکرد جامع در رابطه با محبوب ترین الگوریتم های ارائه شده در این حوزه می باشد که از لحاظ دقت وزن دهی محاسبه می شوند و این کار با استفاده از ماتریس مقایسه فازی صورت می گیرد. چنین تحلیلی بسیار مورد نیاز محققان و متخصصان می باشد. اگرچه هیچ کدام در دسترس نمی باشند. تحلیل های تجربی صورت گرفته و عملکرد الگوریتم های مختلف از طریق 3 پارامتر مختلف مانند اندازه ی ماتریس مقایسه ای، سطح فازی و سطح ناسازگاری ، ارزیابی شده است . ما دریافته ایم که روش حداقل مربعات لگاریتمی اصلاح شده و معکوس فازی روش مجموع ستونی (FICSM) عموما بر دیگر الگوریتم ها برتری دارند ، در حالیکه تجزیه و تحلیل محدوده فازی (FEA) که رایج ترین الگوریتم مورد استفاده می باشد از کمترین دقت برخوردار می باشد. بطور بیشتر، مشاهده می شود که ورژن اصلاح شده ی تحلیل محدوده فازی (FEA) بطور عمده ای عملکرد خود را بهبود داده است.
1.معرفی
متدولوژی های تصمیم گیری چند معیاره (MCDM) تصمیم گیرندگان را در انتخاب بهترین گزینه کمک می کنند در حالیکه اغلب متدهای مختلف و شاخص های متضادی را ارزیابی می نمایند. در طول سالهای گذشته با انجام تحقیقات در رابطه با متدولوژی های تصمیم گیری چند معیاره (MCDM) شاهد رشد در این حوزه بوده ایم (1)و(2). فرایند تحلیل سلسله مراتبی( AHP) که توسط توماس ساتی (3) ارائه شده است، به عنوان مشهور ترین تکنیک های تصمیم گیری چند معیاره (MCDM) در نظر گرفته می شود. (4) فرایند تحلیل سلسله مراتبی( AHP) دیدگاه کارشناسان را در قالب مقایسه های زوجی بررسی می نماید و مقیاس نسبی را در رابطه با ماتریس مقایسه ای بدست می اورد. که ترجیح تصمیم گیرنده را در مورد گزینه های متفاوت ، از لحاظ شاخص و همچنین برتری ، نشان می دهد برای مثال، وزن شاخص ها. امتیاز کلی که وابسته به گزینه های موجود می باشد از طریق مجموع وزنی نرمال شده در شاخص ایجاد می شود و بنابراین تصمیم گیرنده را کمک می کند تا بهترین تصمیم را بگیرد.
6.نتیجه گیری و تحقیقات بیشتر
در این تحقیقات ما عملکرد 9 متد تحلیل سلسله مراتبی فازی ( FAHP) را که 5 متد ان مشهورترین متدهای ارائه شده در ادبیات موضوعی مربوطه می باشند، مقایسه می کنیم. مقدار شاخص سازگاری (CIV ) به عنوان معیار عملکرد به منظور ارزیابی 9 متد تحلیل سلسله مراتبی فازی ( FAHP) بکار گرفته می شود. 3 شرط تجربی به عنوان بخشی از تحلیل در نظر گرفته می شوند که به ترتیب سایز ماتریس (n)، سطوح فازی سازی(الفا)، ناسازگاری (CR)می باشند. برای پارامترهای فازی سازی 4 سطح 0.25و0.50 و 0.75 و 1.00 را در نظر می گیریم. پارامترهای فازی سازی بطور طبیعی به عنوان بخشی از مشکلاتی که تصمیم گیرندگان با ان مواجه می شوند ، نیستند، اما بیشتر متغیرهای تصمیم بخشی از فرایند می باشند. گفته می شود که تحلیل تصمیم می تواند سطوح فازی را و متعاقبا تحلیل سلسله مراتبی فازی ( FAHP) را تنظیم نماید .
Abstract
Analytical Hierarchical Process (AHP) along with fuzzy set theory has been used extensively in the Multi-Criteria Decision Making (MCDM) process in which fuzzy numbers are utilized to represent human judgments more realistically. Over the past couple of decades, numerous articles have been published proposing algorithms through which priority vector (or weight vector) can be calculated from fuzzy comparison matrices. The aim of this study is to conduct a comprehensive performance analysis of the most popular algorithms proposed in this domain in terms of accuracy of weights calculated from fuzzy comparison matrices. Such an analysis is much needed by the researchers and practitioners. However none is available. An experimental analysis is conducted and the performance of various algorithms are evaluated with varying three parameters i.e., the size of the comparison matrix, the level of fuzziness and the level of inconsistency. We found that modified Logarithmic Least Squares Method and Fuzzy Inverse of Column Sum Method (FICSM) generally outperformed other algorithms, while Fuzzy Extent Analysis (FEA) which is the most frequently used algorithm in the literature provides the least accurate results. Furthermore, it was observed that a modified version of FEA method significantly improved its performance.
1. Introduction
Multiple Criteria Decision Making (MCDM) methodologies assist decision makers in choosing the best alternative while evaluating various competing and often conflicting criteria. Over the past many years, literature on MCDM has observed a steady growth [1] [2] while Analytical Hierarchical Process (AHP) proposed by Thomas L. Saaty [3] remains the most popular MCDM technique [4]. AHP seeks expert opinions in the form of pairwise comparisons and later derives ratio scales from comparison matrices which indicate the preferences of the decision maker among different alternatives in terms of the criteria as well as the preference i.e., weights of the criteria themselves. The normalized weighted sum over the criteria provides an overall score associated with each available alternative and thus help decision maker to choose the best decision.
6. Conclusions and future research
In this research we compared performance of nine FAHP methods among which five FAHP methods are the most popular ones in the literature. Compatibility Index Value (CIV) is used as a performance metrics to evaluate all nine FAHP methods. Three experimental conditions are considered as part of the analysis, namely, size of the matrix (n), fuzzification level (α) and inconsistency (C.R). For the fuzzification parameter four levels are assumed as 0.25, 0.50, 0.75 and 1.00. The fuzzification parameter is not inherent to the problem that the decision maker is facing but more a decision variable as part of the process. That is to say, the decision analysts can set the fuzzification level and conduct FAHP accordingly.
چکیده
1.معرفی
2.1. میانگین هندسی و حسابی
2.2 مجموع ستونی
2.3 مجموع ستونی معکوس
2.4. فازی سازی متد فرایند تحلیل سلسله مراتبی( AHP)
3. طراحی تحلیل تجربی
3.1. الگوریتمی برای تولید ماتریس مقایسه ای فازی تصادفی
3.2. معیارهای تجزیه و تحلیل عملکرد
4. نتایج و بحث های محاسباتی
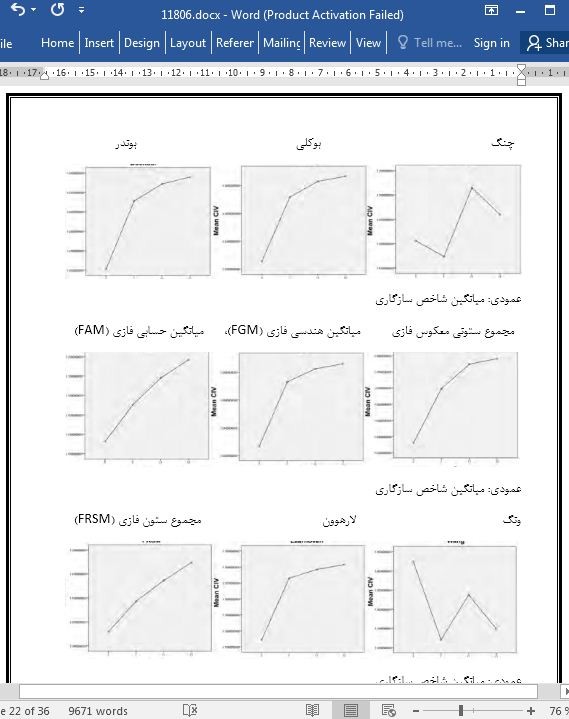
4.1.مقایسه ی تحلیل سلسله مراتبی فازی (FAHP) در 9روش انتخابی
4.2.اندازه ی ماتریس
4.3.پارامترهای فازی
4.4. سطوح ناسازگاری
5.بکارگیری نتایج و ارائه ی چارچوبی برای محققان و متخصصان
6.نتیجه گیری و تحقیقات بیشتر
منابع
Abstract
1. Introduction
2. Fuzzy Analytic Hierarchical Process
2.1. Arithmetic and geometric mean
2.2. Row sum
2.3. Inverse of column sum
2.4. Fuzzification of conventional AHP methods
3. Design of experimental analysis
3.1. Algorithm to generate random fuzzy comparison matrix
3.2. Metrics of performance analysis
4. Computational results and discussions
4.1. Comparison of selected nine FAHP methods
4.2. Matrix size
4.3. Fuzzification parameter
4.4. Inconsistency levels
4.5. Overall analysis for Boender and FICSM
5. Utility of results and proposed framework for researchers and practitioners
6. Conclusions and future research
References
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه