سیستم شبکه عصبی عمیق معادلات دیفرانسیل معمولی
چکیده
هدف این تحقیق استفاده از شبکه های عصبی عمیق برای حل سیستم معادلات دیفرانسیل معمولی است ما با استفاده از کد پیتون یک الگوریتم برداری را ساخته و اجرا کردیم ،همچنین ما آزمایشهای متعددی را انجام دادیم تا بهترین معماری عصبی را انتخاب کنیم .برای یادگیری شبکه عصبی ما از بروزترین روش در کمترین زمان ممکن استفاده کردیم نهایتا ما روش خودمان را با یکی از متدهای مرسوم عددی RK4 مقایسه کردیم ما همچنین نشان دادیم شبکه عصبی می تواند دقت بیشتری برای ماتریس با اعداد کوچکتر فراهم کند .
1. مقدمه
شبکه عصبی عمیق (DNN) توجهات فراوانی را در خصوص حل مسائل مهندسی به خود معطوف کرده است .سیستم معادلات دیفرانسیل معمولی (ODEs) که می تواند پدیده های فیزیکی مختلف را مدل سازی کند از این امتیاز بهره می برد .گرچه روشهای سنتی مرسوم جهت حل سیستم های ODEs وجود دارد اما هر کدام از آنها مزایا و معایب خودشان از نظر دقت ، ثبات،همگرایی و زمان محاسبه و ... را دارند .یکی از معروفترین مدل ها RK4 است .این روش یکی از معدود روشهای مناسب جهت حل مسائل حل ناپذیر است
6. نتیجه گیری و چشم انداز
در این تحقیق ، ما یک الگوریتم برداری برای حل سیستم های ODE با استفاده از DNN ارائه کردیم. ما آزمایش متفاوتی را با استفاده از کد پایتون انجام دادیم و نتیجه را با استفاده از نمودار شبیه سازی کردیم. ما دیدگاهی در مورد ماهیت معماری مدل بدست آورده ایم. ما دیده ایم که برای برخی از مسائل خاص می توانیم دقت لازم را حتی برای یک نورون واحد در لایه مخفی بدست آوریم. اندازه بیشتر نورون دقت بیشتر ، اما تکرار بیشتر برای یادگیری پارامترها را فراهم می کند. علاوه بر این ، افزایش بدون برنامه ریزی نورون سفارش نمی شود. بر اساس این مسئله مهم ، فرد باید بهترین اندازه سلولهای عصبی را تعیین کند.
Abstract
This paper is aimed at applying deep artificial neural networks for solving system of ordinary differential equations. We developed a vectorized algorithm and implemented using python code. We conducted different experiments for selecting better neural architecture. For the learning of the neural network, we utilized the adaptive moment minimization method. Finally, we compare the method with one of the traditional numerical methods-Runge–Kutta order four. We have shown that, the artificial neural network could provide better accuracy for smaller numbers of grid points.
1. Introduction
Deep neural network (DNN) has obtained great attention for solving engineering problems. System of ordinary differential equations (ODEs) that can model various physical phenomena could utilize the advantages of using the method. Though there are well established traditional numerical methods for solving systems of ODEs, they have their own advantages and disadvantages in-terms of accuracy, stability, convergence, computation time etc. One of the well known method is the fourth order Runge–Kutta method (RK4). It is among the finite difference methods well suited for non-stiff problems.
6. Conclusions and outlook
In this paper, we presented a vectorized algorithm for solving systems of ODE using DNN. We conducted different experiment using python code and simulated the result using graphs. We have obtained some insight on the nature of the architecture for the model. We have seen that for some specific problems we can obtain a required accuracy even for a single neuron in the hidden layer. More neuron size provides more accuracy, but more iteration for learning the parameters.
چکیده
1. مقدمه
2. فعالیتهای مرتبط
2.1 شبکه های عصبی عمیق
2.2. فعالیتهای مرتبط با حل معادلات دیفرانسیلی
3. سیستم معادله دیفرانسیل معمولی
4.شبکه عصبی عمیق برای سیستم ODEs
4.1 پیش به سوی انتشار
4.2. الگوریتم برداری
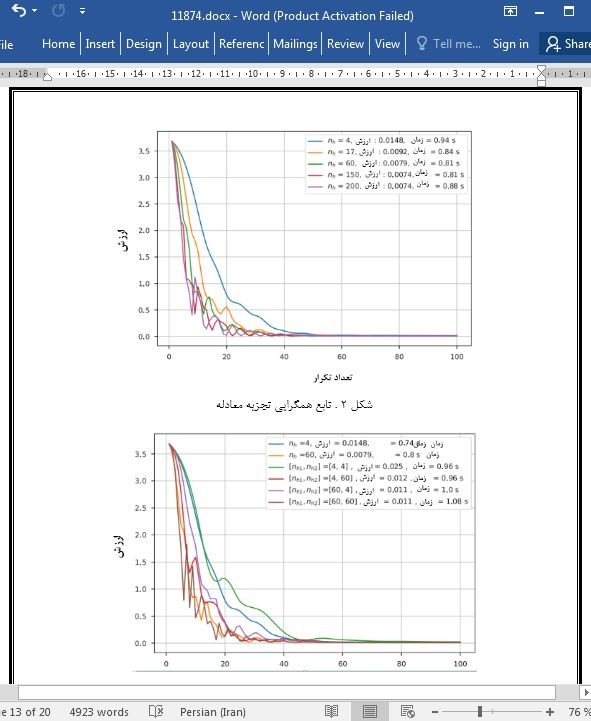
5. پیاده سازی و مقایسه
5.1 آزمایش روی شبکه
5.2. راه حل های عددی
5.3 امتیازات ANN نسبت به روش های RK4
6. نتیجه گیری و چشم انداز
منابع
Abstract
1. Introduction
2. Related works
2.1. Deep neural networks
2.2. Works related to solving differential equations
3. Systems of ordinary differential equation
4. Deep neural network for system of ODEs
4.1. Forward propagation
4.2. The vectorized algorithm
5. Implementation and comparison
5.1. Experiment on the network
5.2. Numerical solutions
5.3. Advantage of ANN over the RK4 methods
6. Conclusions and outlook
References
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه