بررسی عددی و تئوری رفتار لرزه ای دیوارهای طره ای
در این تحقیق، تغییر رفتار دیوارهای طره ای با در نظر گرفتن مسائل مربوط به کارایی نظریه مونونوب – اوکاب و احتمال روی دادن تغییرات فازی در بین حداکثر فشار خاک و نیروهای دورنی در سیستم انجام شده است که هر دو عامل بر طراحی لرزه ای این سازه ها تاثیر می گذارند. برای این منظور، پیش بینی مدل تحلیل و تعادل نیمه استاتیک با نتایج تحقیق عددی گسترده ترکیب شده اند. هر دو تحقیق (نیمه استاتیک و تحلیل دینامیک) در شرایط زلزله واقعی و تکان های ساده داخلی انجام شده اند. نتایج عددی نشان می دهند که حداکثر فشار خاک در ریشه و حداکثر شتاب خمیدگی همیشه در یک فاز هستند و زمانی اتفاق می افتند که نیروهای داخلی از خاکریز دور باشند. مدل مطرح شده پیش بینی خوبی از حداکثر نیروهای داخلی حاصل از زلزله ارائه می کند. نشان داده شده است که فعالسازی احتمالی مکانیزم های ارتجاعی داخل سیستم درقالب لغزشی و عدم مقاومت باعث افزایش قابل توجه در ترکیب کلیدی طراحی لرزه ای یا دیوارهای طره ای می شوند و حداکثر نیروهای داخلی و بزرگ در جابجایی های نهایی کنترل می شوند. نتایج عددی و تئوری برای بیان پیشنهادات مربوط به طراحی لرزه ای دیوارهای طره ای مورد استفاده قرار می گیرد.
مقدمه
دیوارهای بتنی مقاوم سازی شده طره ای کاربرد گسترده ای در طراحی دارند و به عنوان جایگزینی برای دیوارهای گرانشی در نظر گرفته می شوند و رفتار انعطافی عناصر سازه ای با فعالیت تثبیت کننده در حجم خاک و سازه ها ترکیب می شوند. بر خلاف سایر سازه های حایل، مثل پل های طره ای، دیوارهای طره ای دارای محدودیت های جنبشی نیستند و حرکات آنها امکان پیشرفت شرایط محدود در خاک های ثابت را در شرایط استاتیک و دینامیک فراهم می آورد.
نتیجه گیری ها
نتایج عددی ارائه شده در این تحقیق امکان کسب اطلاعات با ارزش در مورد رفتار لرزه ای دیوارهای طره ای نهایی را در قالب جابحایی های موقت مورد انتظار و حداکثر نیروهای داخلی و همچنین امکان اعتبار سنجی پیش بینی های انجام شده در مورد مدل شبه استاتیک را بر اساس روشهای تحلیل/ تعادل محدود فراهم می آورد.
همان طور که اخیرا برای موضوع انواع سازه های حایل نهایی مشاهده شده است (کانتی و همکارانش 2013و2014)، رفتار دینامیک دیوارهای حایل عمدتا تحت تاثیر مقاومت سیستم قرار می گیرد، در حالی که انعطاف پذیری دیوار و مقاومت خاک نقش مهمی ایفا می کنند. یکی از عواقب مستقیم این مشاهده این است که شتاب بحرانی می تواند یکی از فاکتورهای کلیدی برای طراحی لرزه ای، کنترل حداکثر نیروهای داخلی و جابجایی های نهایی باشد.
This paper provides an interpretation of the dynamic behaviour of yielding cantilever walls, regarding which open issues still remain about the applicability of the Mononobe–Okabe theory and the possible occurrence of phase shift between the maximum soil thrust and the inertia forces into the system, which both affect the seismic design of these structures. To this end, the predictions of a pseudostatic limit equilibrium/analysis model are combined with the results of an extensive numerical study, with both pseudostatic and dynamic analyses performed under real earthquakes and simple input motions. Numerical outcomes show that the maximum soil thrust on the stem and the maximum bending moment are always in phase and occur when the inertia forces are away from the backfill. The proposed model provides a good prediction of the maximum internal forces induced by the earthquake. It is shown that the possible activation of plastic mechanisms within the system, in the form of either sliding or bearing failure, makes the critical acceleration a key ingredient for the seismic design of cantilever walls, controlling both the maximum internal forces and the magnitude and trend of final displacements. Numerical and theoretical findings are used to provide suggestions for the seismic design of cantilever walls.
INTRODUCTION
Reinforced concrete cantilever walls are widely used in design practice as an alternative to gravity walls, combining the flexural behaviour of the structural elements with the stabilising action of the soil mass above the footing slab. In contrast to other types of retaining structures, such as basement walls or bridge abutments, yielding cantilever walls do not have kinematic constraints and their movements permit the development of active limit conditions in the retained soil, both under static and dynamic conditions.
CONCLUSIONS
The numerical results presented in this paper made it possible both to gain valuable information on the seismic behaviour of yielding cantilever walls, in terms of expected permanent displacements and maximum internal forces, and to validate the predictions of a simple pseudostatic model, based on limit equilibrium/analysis methods.
As already observed for other types of yielding retaining structures (Conti et al., 2013, 2014), the dynamic behaviour of cantilever walls is primarily governed by the strength of the system, while the wall flexibility and the soil stiffness play a minor role. A direct consequence of this observation is that the critical acceleration turns out to be the key ingredient for their seismic design, controlling both the maximum structural internal forces and the final displacement.
مقدمه
پیش زمینه تئوری و افزایش مهم
طرح مسئله و روشهای تحلیل
مدل عددی
روش تحلیل
تحلیل شبه استاتیک
مکانیزم های ارتجاعی
توزیع فشار شبه استاتیک
تحلیل دینامیک
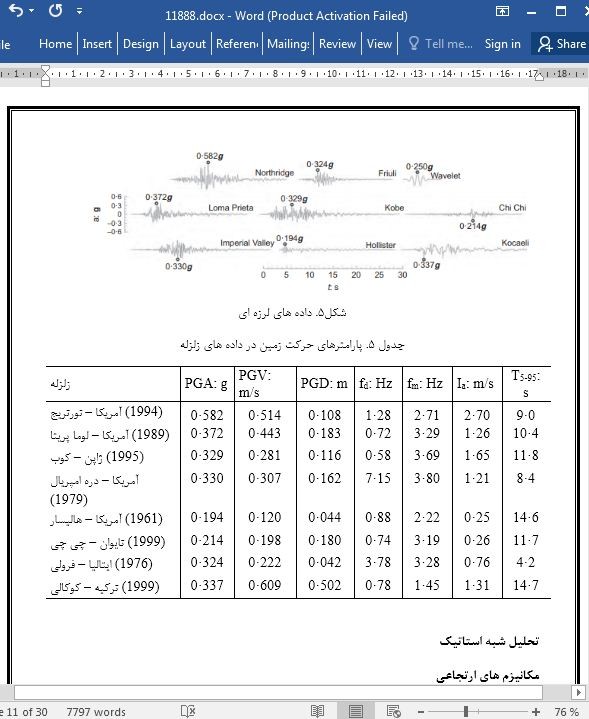
سیگنال های ورودی موج های کوچک
بحث در مورد نتایج
نتیجه گیری ها
ضمیمه
نمادها
منابع
INTRODUCTION
THEORETICAL BACKGROUND AND CRITICAL ACCELERATION
PROBLEM LAYOUT AND ANALYSIS PROCEDURE
Numerical model
Procedure for analysis
Seismic input
PSEUDOSTATIC ANALYSES
Plastic mechanisms
Pseudostatic stress distribution
DYNAMIC ANALYSES
Wavelet input signals
Real input earthquakes
DISCUSSION OF RESULTS
CONCLUSIONS
ACKNOWLEDGEMENT
APPENDIX
REFERENCES
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه