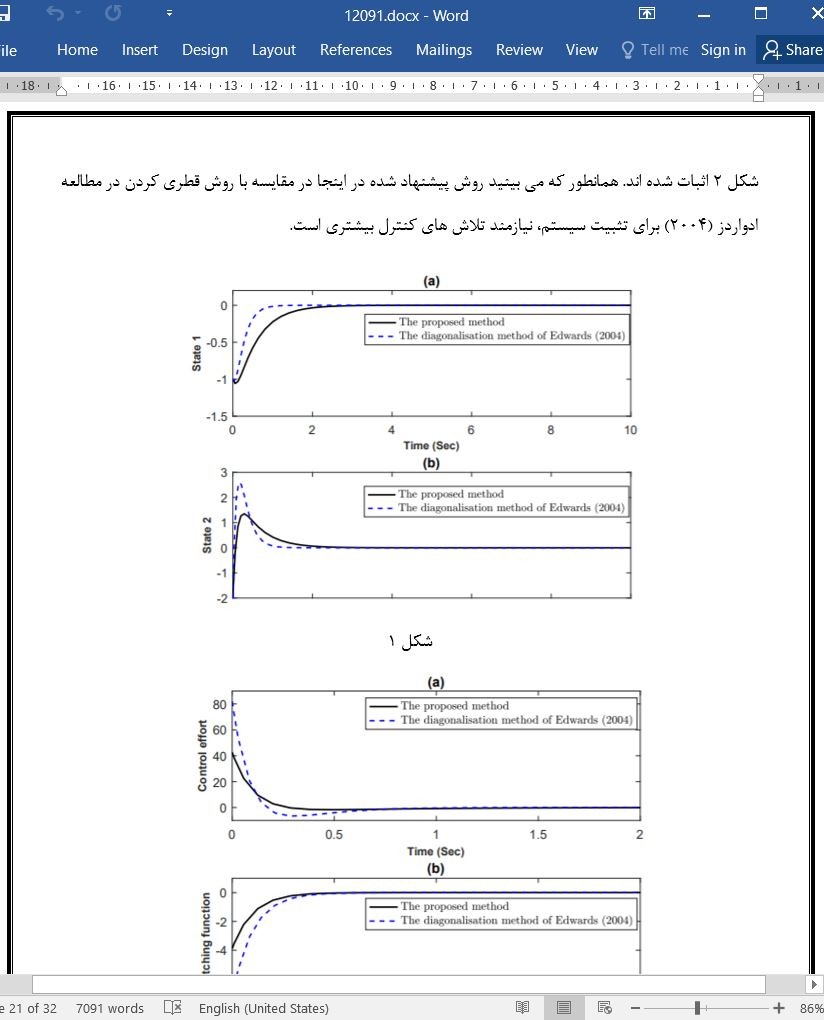
طراحی کنترل مود لغزشی بهینه با استفاده از تخصیص ساختار خاص جزئی
ما در این مقاله چارچوب جدیدی را برای طراحی یک سطح لغزشی (کشویی) برای یک سیستم معین توصیف میکنیم و در عین حال عملکردهای H2 چند کاناله سیستم حلقه بسته را تحت کنترل می گیریم. برعکس، در این روش برای اغلب الگوهای طراحی سطح لغزشی جاری، سطح تلاش کنترل مورد نیاز برای حفظ لغزش کاهش می یابد. روش پیشنهادی برای طراحی کنترل مود لغزشی بهینه در دو مرحله اجرا میشود. در مرحله اول یک بهره فیدبک حالت با استفاده از یک طرح مبتنی بر LMI (نابرابرreduced-orderی ماتریس خطی) استخراج میشود که میتواند تعدادی از مقادیر مشخصه حلقه بسته را به یک مقدار معلوم تخصیص دهد و در عین حال از ملزومات عملکردی پیروی کند. ماتریس تابع لغزشی مربوط به فیدبک حالت خاص استخراج شده در مرحله اول، در مرحله دوم با استفاده از یکی از دو روش موجود بدست می آید (که به همین منظور توسعه داده شده اند). تئوری پیشنهاد شده با استفاده از مثالهای عددی ارزیابی میگردد: بعنوان مثال مسئله ردگیری خروجی حالت ماندگار از طریق یک کنترل مود لغزشی (SMC) فیدبک حالت برای کنترل پرواز.
1. مقدمه
کنترل مود لغزشی (SMC) یک روش کنترل است که بعلت خواص مقاوم بودن خود در برابر عدم قطعیت های تطبیق یافته، روز به روز در کاربردهای مختلف بیشتری مورد استفاده قرار میگیرد (آرگا، لی، سو و نگویِن 2016 ب؛ ادواردز 2004؛ ادواردز و اسپورجن 1998؛ هرمَن، اسپورجن و ادواردز 2001؛ هو، وانگ و گائو 2008؛ اوتکین 1992). تقریباً تمام روشهای طراحی کنترل مود لغزشی سنتی از دو مرحله جداگانه تشکیل شده اند. در مرحله اول یک سطح لغزشی مناسب انتخاب میشود بطوریکه میتواند یک حرکت لغزشی مرتبه کاهش یافته را با دینامیک مناسب تضمین کند. رویکردهای بسیاری برای این منظور توسعه داده شده اند؛ بعنوان مثال روشهای جایابی قطبی و کوادراتیک بهینه (ادواردز و اسپورجن 1998)، و نابرابری ماتریس خطی (LMI) (آرگا، لی، سو و نگوین 2016 الف؛ چوی 2002؛ هرمن و همکارانش 2001؛ پارک، چوی و کونگ 2007). در مرحله دوم با پیروی از این موضوع، کنترلری را برای ترغیب و حفظ حرکت لغزشی طراحی میکنیم. با اینحال این روشهای طراحی سنتی قادر نیستند که عمل کنترل موجود مورد نیاز برای تحقق هدف کنترل را محدود سازند. دلیل این مسئله این است که در طی ترکیب تابع راه گزینی، هیچ حسی از سطح عمل کنترل مورد نیاز برای ترغیب و حفظ لغزش وجود ندارد (ادواردز 2004). اگر در طی روند طراحی هیچ محدودیتی بر روی اعمال کنترل در نظر گرفته نشود یک سطح راه گزینی کاملاً غیرعملی (و در نتیجه یک قانون کنترل) را میتوان استخراج کرد چون ممکن است برای رسیدن به سطح لغزش و حفظ آن به سطح بالایی از تلاش های کنترل نیاز پیدا کنیم.
This paper describes a new framework for the design of a sliding surface for a given system while multi-channel H2 performances of the closed-loop system are under control. In contrast to most of the current sliding surface design schemes, in this new method the level of control effort required to maintain sliding is penalised. The proposed method for the design of optimal sliding mode control is implemented in two stages. In the first stage, a state feedback gain is derived using an LMI-based scheme that can assign a number of the closed-loop eigenvalues to a known value whilst satisfying performance specifications. The sliding function matrix related to the particular state feedback derived in the first stage is obtained in the second stage by using one of the two different methods developed for this goal. The proposed theory is evaluated by using numerical examples including the problem of steady state output tracking via a state-feedback SMC for flight control.
1. Introduction
Sliding mode control (SMC) is a control method which, due to its robustness properties against matched uncertainties, has progressively been used in different applications (Argha, Li, Su, & Nguyen, 2016b; Edwards, 2004; Edwards & Spurgeon, 1998; Herrmann, Spurgeon, & Edwards, 2001; Hu, Wang, & Gao, 2008; Utkin, 1992). Roughly speaking, all the traditional SMC design methods consist of two separate stages. In the first stage, an appropriate sliding surface is chosen so that it can guarantee a reduced-order sliding motion with suitable dynamics. Many approaches have been developed for this goal; for example, pole placement and optimal quadratic (Edwards & Spurgeon, 1998), and linear matrix inequality (LMI) methods (Argha, Li, Su, & Nguyen, 2016a; Choi, 2002; Herrmann et al., 2001; Park, Choi, & Kong, 2007). Following this, the second stage designs a controller to persuade and retain the sliding motion. However, these traditional design methods are unable to limit the available control action required for satisfying the control objective. This is because, during the switching function synthesis, there is no sense of the level of the control action required to persuade and retain sliding (Edwards, 2004). If no limits are considered on the control actions during the design procedure, a very impractical switching surface and thereby control law may always be derived, as the high level of control efforts may be required to reach the sliding surface and maintain there thereafter.
1. مقدمه
2. صورت مسئله و مقدمات
3. مسئله تخصیص ساختار خاص جزئی برای طراحی کنترل مود لغزشی بهینه
3.1 مشخص سازی نابرابری ماتریس خطی H2
3.2 استفاده از مشخص سازی نابرابری ماتریس خطی بهبود یافته برای فیدبک حالت H2 چند کاناله
3.3 تخصیص ساختار خاص جزئی
4. بدست آوردن ماتریس تابع راه گزینی
4.1 رویکرد 1: رویکرد مستقیم
4.2 رویکرد 2: رویکرد غیرمستقیم
5. خلاصه طرح پیشنهادی
6. مثالهای عددی
6.1 مثال 1
6.2 مثال 2
6.3 مثال 3: کنترل پرواز
6.4 یک آزمایش: کنترل یک سیستم آونگی چرخشی
7. نتیجه گیری ها
منابع
1. Introduction
2. Problem Statement and Preliminaries
3. Partial Egienstructure Assignment Problem For Optimal SMC Design
3.1 H2 LMI characterization
3.2 Multi-channel H2 state feedback using improved LMI characterisations
3.3 Partial eigenstructure assignment
4. Obtaining The Switching Function Matrix
4.1 Approach 1: direct approach
4.2 Approach 2: indirect approach
5. The Summary of the Proposed Scheme
6. Numerical examples
6.1 Example 1
6.2 Example 2
6.3 Example 3: Flight control
6.4 An experiment: control of a rotary pendulum system
7. Conclusions
References
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه