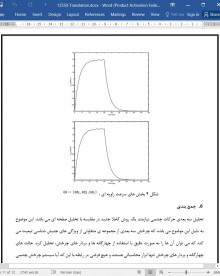
مدل سازی دینامیک سیستم اکلومتر ( بررسی حرکات چشمی) در سه بعد
چکیده
کنترل کردن نگاه خیره در سه بعد با استفاده از آرایش هندسی عضله های خارج چشمی به دست آمده است. برای حرکات جهشی با حالت ثابت سر، محور چرخش چشم بر اساس قانون لیستینگ (وقتی پلک از حالت استراحت به حرکت درمیآید در حالت دوم زاویه چرخشی مساوی زاویهای خواهد بود که چشم در حول یک محور ثابت عمود بر خط بینائی حالات اول و دوم گردش کند) محدود می شود. در این مقاله، یک مدل چشمی برای کنترل کردن نگاه خیره مورد استفاده قرار گرفته است. حالت های چهار گانه مرتبط با جایگاه چشم و چرخش های آن برای توصیف دقیق محور چرخش مورد استفاده قرار می گیرد.
1. مقدمه
تفکیک بهینه ی بصری در شبکیه چشم برای اهداف مرتبط با حفره چشمی( قسمت مرکزی شبکیه چشم) به دست آمده است. به دلیل این که قسمت مرکزی شبکیه دارای قطر کمی می باشد ( کمتر از یک درجه) ، هر زمان که سیستم بصری ، اهداف بصری را جست جو می کند، خط خیرگی باید دقیقا مطابق با شی باشد. این چنین حرکاتی در حالت خیرگی بر اساس سیستم حرکت جهشی کنترل می شود. با این وجود به صورت عمومی، تغییرات در حالت خیرگی به منظور رسیدن به هدف بصری خاص را می توان با استفاده از ترکیب های مختلف چشم، سر و چرخش های بدن به دست آورد و ما در این مطالعه، بر روی حالتی تمرکز داریم که سر حالت ثابتی دارد.
6. جمع بندی
تحلیل سه بعدی حرکات چشمی نیازمند یک روش کاملا جدید در مقایسه با تحلیل صفحه ای می باشد. این موضوع به دلیل این موضوع می باشد که چرخش سه بعدی از مجموعه ی متفاوتی از ویژگی های جنبش شناسی تبعیت می کند که می توان آن ها را به صورت دقیق با استفاده از چهارگانه ها و بردار های چرخش، تحلیل کرد. حالت های چهارگانه و بردار های چرخش تنها ابزار محاسباتی هستند و هیچ فرضی در رابطه با این که آیا سیستم چرخش چشمی از آن ها استفاده می کند یا خیر مورد نیاز نمی باشد و می توان تنها با استفاده از آن ها برای ارائه ی جایگاه ها و چرخش های چشمی استفاده کرد. همچنین با استفاده از این ابزار می توان قوانین داندرز و لیستینگ را هم بهتر توصیف کرد.
Abstract
Gaze control in three dimensions is achieved by the geometrical arrangement of the extra-ocular muscles. For head-fixed saccadic eye movements, the ocular rotation axis is constrained according to Listing's law. In this paper, an ocular model is developed to control gaze. Quaternions associated with eye positions and rotations are used to precisely describe the axis of rotation.
I. INTRODUCTION
The optimal visual resolution in retina is achieved for targets projected on the fovea (central part of the retina). Since the fovea has a small diameter (less than a degree), whenever the visual system starts exploring the visual target, the gaze line must be precisely aligned with the object. Such a movement in gaze is controlled by the saccadic system. Although in general, goal-directed gaze shifts may be achieved by many different combinations of eye-, head-, and body rotations, the study here is focused on the head fixed saccades.
VI. CONCLUSION
Three-dimensional analysis of eye movements needs a whole new approach compared to planer analysis (for planer models, see [10] and [8]). This is due to the fact that 3D rotations follow a different set of kinematic properties which could elegantly be analyzed using quaternions and rotation vectors. Quaternions and rotations vectors are merely a computational tool and no assumptions needed regarding whether the oculomotor system uses them to represent eye positions and rotations. Also the Donder’s and Listing’s laws are better explained using them.
چکیده
1. مقدمه
2. ماتریس های چرخش، حالت های چهار گانه و بردار های چرخش
3. قانون داندرز و قانون لیستینگ
4. مدل سه بعدی چشم
5. نتایج
6. جمع بندی
منابع
Abstract
1. INTRODUCTION
2. ROTATION MATRICES, QUATERNIONS AND ROTATION VECTORS
3. DONDER’S LAW AND LISTING’S LAW
4. 3D MODEL OF THE EYE
5. RESULTS
6. CONCLUSION
REFERENCES
- اصل مقاله انگلیسی با فرمت ورد (word) با قابلیت ویرایش
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه