دانلود مقاله درباره فشرده سازی مدل های عمیق به وسیله رتبه پایین و تجزیه تنک
1. مقدمه
یادگیری عمیق در زمینههای مختلفی از جمله طبقهبندی تصویر [15، 23، 25، 9] و تشخیص شی [21] بهبود چشمگیری داشته است. با این حال، محاسبات شدید و نیازمندیهای حافظه از اکثر مدلهای عمیق، استفاده از دستگاههای روزمره با فضای ذخیرهسازی کم و قابلیتهای محاسباتی ضعیف مانند تلفنهای همراه و دستگاههای تعبیهشده را محدود میسازد. این محدودیتها سبب انگیزه پژوهشگران شده است تا بدین شکل از افزونگی ذاتی موجود در پارامترها و نقشههای ویژگی در مدلهای عمیق استفاده کنند. به طور کلی این افزونگی در ماهیت ساختاری ماتریسهای وزنی و نقشههای ویژگی منعکس شده است [3، 24]. با حذف افزونگی، منابع را میتوان بدون تاثیرگذاری بر ظرفیت و قابلیت تعمیم اکثر مدلهای عمیق حفظ کرد.
تنکی و رتبههای پایین به عنوان مفروضات ساختارهای حیاتی در کارهای قبلی برای حذف افزونگی هستند. نخست، هرسسازی یک استراتژی ساده برای حذف پارامترهای همبسته و نورونهای مشترک تطبیقی است و برای کسب ساختارهای تنک است. برای مثال، لیکون و همکاران [16] اطلاعات مشتق درجه دوم برای هدایت فرآیند حذف وزنهای غیرمهم استفاده کردند. هان و همکاران [8] به آموزش مجدد تکرارشونده یک مدل تنک شده با حذف وزن بیاهمیت با استفاده از روش آستانهسازی سخت پرداختند. هی و همکاران [10] از مقیاسهایی مانند هنجار l1 از وزنهای غیرپیوندی برای شناسایی نورونهای غیر ضروری استفاده کردند. ماریس و سرا [19] به نمونهبردرای از غیرهمبستهترین نورونها با فرآیندهای تعیین نقطه پرداختند و سایر نورونها با همبستگی بسیار بالا را حذف کردند. فرض ساختاری دیگری در حالت فاقد رتبه پایین است. وزنها در لایههای پیچشی و کامل متصل شده را میتوان توسط فیلترهای تقریب رتبهپایین کاهش داد [4، 27، 14]. ژانگ و همکاران [30] یک زیر فضای رتبهپایین برای بردارهای ویژگی را ارائه دادند که منجر به تجزیه ماتریس وزن، کاهش پارامتر و زمان تست سریعتر شده بود.
7. نتیجهگیری
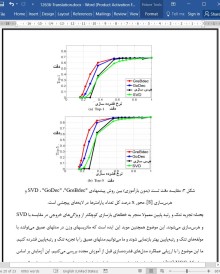
در این مقاله ما چارچوب فشردهسازی عمیق یکپارچهای را پیشنهاد دادیم که به تجزیه ماتریسهای وزن به مولفههای وزنی و رتبهپایین میپرداخت. در قیاس با SVD های سنتی و روشهای هرسسازی، مدل پیشنهادی به طور قابل توجهی سبب بهبود عملکرد پیش از آموزش مجدد میشود به خصوص زمانی که بازسازیهای نقشه ویژگی درون چارچوب ادغام شده است. این عملکرد بالا مقداردهی اولیه بهتری را برای آموزشهای مجدد بعدی فراهم میسازد که به مدل پیشنهادی ما برای دستیابی به نرخ فشردهسازی بالاتری بدون از دست رفتن دقت برای بسیاری از مدلهای محبوب کمک میکند. ما حداکثر میتوانیم در حدود 15 برابر فضای ذخیرهسازی را حفظ کنیم که بدین شکل روش ما بسیاری از رویکردهای جدید که به استفاده از یک استراتژی میپرداختند را شکست میدهد.
1. Introduction
Deep learning has delivered significant improvements in several fields including image classification [15, 23, 25, 9] and object detection [21]. However, the intensive computational and memory requirements of most deep models limit their deployment on daily use devices with low storages and computing capabilities such as cellphones and embedded devices. This limitation has motivated researchers to exploit the intrinsic redundancy found in parameters and feature maps in deep models. Generally, this redundancy is reflected in the structured nature of the weight matrices and feature maps [3, 24]. By removing the redundancy, resources can be saved without affecting the capacity and generalizability of most deep models.
Sparsity and low-rankness independently acted as vital structure assumptions in the previous work for redundancy removal. First, pruning is a straightforward strategy to remove correlated parameters and co-adapted neurons, and to obtain sparse structures. For example, LeCun et al. [16] used the second derivative information to guide the removal of unimportant weights. Han et al. [8] repeatedly retrained a sparsified model with unimportant weights removed using a hard thresholding method. He et al. [10] used measures like l1 norm of out-linked weights to identify unimportant neurons. Mariet and Sra [19] sampled the most uncorrelated neurons by the determinant point processes, and removed other highly correlated neurons. Another structure assumption is the low-rankness. Weights in the convolutional and fully connected layers can be reduced by approximating low-rank filters [4, 27, 14]. Zhang et al. [30] estimated a low-rank subspace for the feature vectors that resulted in weight matrix decomposition, parameter reduction, and faster testing time.
7. Conclusion
Here we propose a unified deep compression framework that decomposes weight matrices into their low-rank and sparse components. Compared to traditional SVDs and pruning methods, the proposed model significantly improves the performance prior to retraining, especially when feature map reconstructions are integrated into the framework. This high performance provides a better initialization for the subsequent retraining, which helps the proposed model to achieve high compression rates without loss of accuracy for many popular models. We can save at most 15× storage space, which beats many recent methods using a single strategy
چکیده
1. مقدمه
2. کار مرتبط
3. مدل فشردهسازی عمیق
4. بهینهسازی
5. تجزیه و تحلیل نظری
6. آزمایشات
1. 6 تجزیه و تحلیل در کل شبکهها
2 .6 تجزیه و تحلیل در لایههای پیچشی
7. نتیجهگیری
منابع
Abstract
1. Introduction
2. Related Work
3. Deep Compression Model
4. Optimization
5. Theoretical Analysis
6. Experiments
6.1. Analysis on the Whole Networks
6.2. Analysis on the Convolutional Layers
7. Conclusion
References
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه