دانلود مقاله یافتن خوشه هایی با اندازه، شکل و چگالی های مختلف در داده های آشفته با ابعاد بالا

چکیده
     مساله یافتن خوشه ها در داده ها هنگامیکه خوشه ها با اندازه، شکل و چگالی های مختلف وجود دارند و هنگامیکه داده ها شامل میزان زیادی از داده های آشفته و پرت هستند چالش برانگیز می باشد. بسیاری از این مشکلات مخصوصا هنگامیکه داده ها با ابعاد بسیار بالا، مانند داده های متنی و سری زمانی وجود دارند، حتی قابل توجه تر می شوند. در این مقاله، ما یک تکنیک خوشه بندی جدید را ارائه می کنیم که این مشکلات را حل می کند. الگوریتم ما درابتدا نزدیکترین همسایه های هر نقطه داده را پیدا می کند و سپس شباهت بین هر جفت از نقاط را برحسب تعداد نزدیکترین همسایه ای که در دو نقطه مشترک هستند مجددا تعریف می کند. با استفاده از این تعریف شباهت، ما داده های آشفته و پرت را حذف می کنیم، نقاط محوری را شناسایی می کنیم و سپس خوشه ها را حول نقاط محوری می سازیم. استفاده از یک تعریف نزدیکترین همسایه مشترک شباهت مشکل چگالی متغیر را حل می کند، درحالیکه استفاده از نقاط مرکزی مشکل مربوط به شکل و اندازه را برطرف می کند. به طور تجربی نشان می دهیم که الگوریتم ما بهتر از روش های سنتی (مانند K-میانگین) در انواع مجموعه داده ها، مانند داده های نفوذ شبکه KDD Cup '99، داده سری های زمانی علوم زمینی NASA و مجموعه نقاط دوبعدی، عمل می کند. درحالیکه الگوریتم ما می تواند خوشه هایی با چگالی بالا را همانند الگوریتم های خوشه بندی دیگر پیدا کند، می-تواند خوشه هایی را که این روش ها نادیده می گیرند، یعنی خوشه هایی با چگالی پایین و متوسط را نیز پیدا کند، که این خوشه ها مهم هستند چونکه آن ها نواحی نسبتا یکنواخت احاطه شده توسط ناحیه های غیریکنواخت یا با چگالی بالاتر را ارائه می کنند. پیچیدگی زمان اجرای تکنیک ما  است چونکه ماتریس شباهت باید ساخته شود. اما، تعدادی از بهینه سازی ها را بحث می کنیم که به الگوریتم کنترل مجموعه داده های بزرگ به طور موثر اجازه می دهند. برای مثال، 100000 سند از مجموعه TREC می توانند در یک ساعت در یک کامپیوتر رومیزی خوشه بندی شوند.

1- مقدمه
     تحلیل خوشه ای ]8،11[ داده ها را به گروه ها (خوشه ها) به منظور خلاصه سازی یا درک بهتر تقسیم می کند. برای مثال، تحلیل خوشه ای برای جستجو در گروه های مربوط به اسناد، برای یافتن ژن ها و پروتئین هایی که عملکرد مشابه دارند، یا به منظور متراکم سازی داده استفاده شده است. درحالیکه خوشه سازی تاریخچه طولانی دارد و تکنیک های خوشه بندی زیادی در آمار، تشخیص الگو، داده کاوی و زمینه های دیگر ایجاد شده اند، هنوز چالش های قابل توجهی باقی مانده اند. تاحدی، به خاطر این است که مجموعه داده های بزرگ و با ابعاد بالا و توان محاسباتی برای سروکار داشتن با آن ها نسبتا جدید است. اما، بیشتر چالش های خوشه بندی، مخصوصا آن هایی که مربوط به کیفیت به جای منابع محاسباتی هستند، همان چالش هایی هستند که دهه های قبلی وجود داشته اند: چگونگی کنترل داده های آشفته و پرت، چگونگی تعیین تعداد خوشه ها و چگونگی یافتن خوشه هایی با اندازه، شکل ها و چگالی های مختلف. به این دلیل، اگرچه مقیاس پذیری تمرکز اصلی بیشتر کار خوشه بندی در داده کاوی بوده است، تحقیق خوشه بندی نیز متمرکز بر این موضوعات دیگر بوده است.

7- نتیجه گیری و کار آینده
     در این مقاله، ما یک الگوریتم خوشه بندی نزدیکترین همسایه مشترک جدید را توصیف کردیم که می تواند خوشه هایی با شکل، اندازه و چگالی متفاوت را حتی در حضور داده های آشفته و پرت پیدا کند. این الگوریتم می-تواند به طور همزمان با داده هایی با چگالی های متفاوت سروکار داشته باشد و به طور خودکار تعداد خوشه ها را تعیین کند. بنابراین، باور داریم که الگوریتم ما یک جایگزین قدرتمند را برای بسیاری از روش های خوشه بندی دیگر فراهم می کند در انواع داده و خوشه هایی که می توانند سروکار داشته باشند محدود هستند.
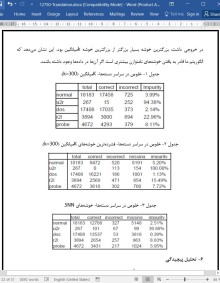
     به ویژه، الگوریتم خوشه بندی SNN ما می تواند خوشه هایی را پیدا کند که نواحی نسبتا یکنواختی را با توجه به پیرامون خودشان ارائه می کنند، حتی اگر این خوشه ها با چگالی پایین یا متوسط باشند. مثالی از این مورد را در زمینه سری های زمانی علوم زمینی NASA ارائه کردیم، که در آن روش الگوریتم خوشه بندی ما قادر به یافتن همزمان خوشه هایی با چگالی های متفاوت است که برای توصیف چگونگی تاثیر اقیانوس بر سطح زمین مهم بودند. DBSCAN تنها می تواند خوشه های ضعیف تر را با فدا کردن کیفیت خوشه های قوی تر پیدا کند. Kمیانگین می تواند خوشه ضعیف تر، ولی تنها به صورت یکی از تعداد زیاد خوشه ها پیدا کند. به علاوه، چونکه کیفیت این خوشه در جملات Kمیانگین پایین بود، هیچ راهی برای شناسایی این خوشه به صورت مورد خاص وجود نداشت.

ABSTRACT

     The problem of finding clusters in data is challenging when clusters are of widely differing sizes, densities and shapes, and when the data contains large amounts of noise and outliers. Many of these issues become even more significant when the data is of very high dimensionality, such as text or time series data. In this paper we present a novel clustering technique that addresses these issues. Our algorithm first finds the nearest neighbors of each data point and then redefines the similarity between pairs of points in terms of how many nearest neighbors the two points share. Using this new definition of similarity, we eliminate noise and outliers, identify core points, and then build clusters around the core points. The use of a shared nearest neighbor definition of similarity removes problems with varying density, while the use of core points handles problems with shape and size. We experimentally show that our algorithm performs better than traditional methods (e.g., K-means) on a variety of data sets: KDD Cup '99 network intrusion data, NASA Earth science time series data, and two dimensional point sets. While our algorithm can find the “dense” clusters that other clustering algorithms find, it also finds clusters that these approaches overlook, i.e., clusters of low or medium density which are of interest because they represent relatively uniform regions “surrounded” by non-uniform or higher density areas. The run-time complexity of our technique is O(n2 ) since the similarity matrix has to be constructed. However, we discuss a number of optimizations that allow the algorithm to handle large datasets efficiently. For example, 100,000 documents from the TREC collection can be clustered within an hour on a desktop computer.

1. INTRODUCTION

     Cluster analysis [8,11] divides data into groups (clusters) for the purposes of summarization or improved understanding. For example, cluster analysis has been used to group related documents for browsing, to find genes and proteins that have similar functionality, or as a means of data compression. While clustering has a long history and a large number of clustering techniques have been developed in statistics, pattern recognition, data mining, and other fields, significant challenges still remain. In part, this is because large, as well as high dimensional, data sets and the computational power to deal with them are relatively recent. However, most of the clustering challenges, particularly those related to “quality,” rather than computational resources, are the same challenges that existed decades ago: how to handle to noise and outliers, how to determine the number of clusters, and how to find clusters with differing sizes, shapes and densities. For this reason, although scalability has been the main focus of much of the clustering work in data mining, clustering research has also focused on these other issues.

7. CONCLUSIONS AND FUTURE WORK

     In this paper we described a novel shared nearest neighbor clustering algorithm that can find clusters of varying shapes, sizes, and densities, even in the presence of noise and outliers. The algorithm can simultaneously handle data of varying densities, and automatically determines the number of clusters. Thus, we believe that our algorithm provides a robust alternative to many other clustering approaches that are more limited in the types of data and clusters that they can handle.

     In particular, our SNN clustering algorithm can find clusters that represent relatively uniform regions with respect to their “surroundings,” even if these clusters are of low or medium density. We presented an example of this in the context of NASA Earth science time series data, where our SNN clustering approach was able to simultaneously find clusters of different densities that were important for explaining how the ocean influences the land. DBSCAN could only find the “weaker” cluster by sacrificing the quality of the “stronger” clusters. Kmeans could find the weaker cluster, but only as one of a large number of clusters. Furthermore, since the quality of this cluster was low in K-means terms, there was no way to identify this cluster as being anything special.

(جهت بزرگ نمایی روی عکس کلیک نمایید)

چکیده
1- مقدمه
1-1 چالش های تحلیل خوشه ای و کار مرتبط
1-2 کار ما 
1-3 طرح کلی این مقاله
2- یک تعریف بهتر از شباهت
3- یک تعریف بهتر از چگالی
4- یک الگوریتم خوشه بندی نزدیک ترین همسایه مشترک
4-1 شناسایی نقاط محوری و حذف آشفتگی
4-2 الگوریتم خوشه بندی SNN
5- مطالعات تجربی
5-1 داده های دوبعدی
5-2 داده های علوم زمینی NASA
5-3 داده های نفوذ به شبکه KDD CUP ‘99
6- تحلیل پیچیدگی
7- نتیجه گیری و کار آینده
منابع

ABSTRACT
1. INTRODUCTION
1.1. The Challenges of Cluster Analysis and Related Work
1.2. Our Contribution
1.3. Outline of the Paper
2. A BETTER DEFINITION OF SIMILARITY
3. A BETTER DEFINITION OF DENSITY
4. A SHARED NEAREST NEIGHBOR CLUSTERING ALGORITHM
4.1. Identifying Core Points and Removing Noise
4.2. The SNN Clustering Algorithm
5. EXPERIMENTAL STUDIES
5.1. 2D Data
5.2. NASA Earth Science Data
5.3. KDD Cup ’99 Network Intrusion Data
6. COMPLEXITY ANALYSIS
7. CONCLUSIONS AND FUTURE WORK
REFERENCES