دانلود مقاله برآورد پارامترهای مدل ون-گنوختن برای منحنی نگهداری آب خاک توسط الگوریتم های هوشمند
1- مقدمه
منحنی نگهداری آب خاک (SWRC)، که رابطه بین محتوای آب خاک و پتانسیل هیدرولیکی را تعریف می کند، یک خصوصیت فیزیکی مهم ماده خاک می باشد [1]. SWRC هنگام مطالعه فرآیندهای جریان آب و مدل سازی آب و حرکت محلول در یک خاک اشباع نشده یا هنگام محاسبه موجودیت آب برای گیاهان ضروری است [2]. فرمول های تجربی بطور گسترده برای توصیف SWRC استفاده می شوند، جاییکه معادله ون-گنوختن (VG) تقریبا برای تمام بافت های خاکی مناسب است [3]. اما، چهار پارامتر مستقل نیاز است که در معادله VG تعیین شوند، و انطباق پارامتر در حل مسائل غیرخطی شامل می شود. روش حداقل مربعات رایج نه تنها وابستگی بالایی به مقدار اولیه پارامتر دارد، بلکه پدیده اتمام الگوریتم و مقدار منفی را ایجاد می کند.
محققان بسیاری برای حل این مسائل تلاش کرده اند، که عمدتا به چهار نوع زیر تقسیم می شوند.
(1) الگوریتم های بهینه سازی مانند روش سیمپلکس غیرخطی، روش تکرار پیکارد، روش تکاملی سیمپلکس و حداقل مربعات میرایی خطی برای انطباق پارامترهای مدل VG استفاده شدند [4،5].
(2) برنامه کامپیوتری، RETC[3]، سیستم پردازش داده (DSP) و جعبه ابزار تابع غیرخطی MATLAB[6] برای برآورد پارامترهای معادله VG استفاده شدند. اما، روش های (1) و (2) بالا وابستگی شدیدی به مقادیر اولیه پارامترها دارند. برای روش حداقل مربعات نیز همین برقرار است.
6- نتیجه گیری
یک بهینه سازی ازدحام ذرات تعمیم یافته (IPSO) در این مطالعه ارائه شد. الگوریتم های هوشمند مانند IPSO، GA و SA برای تعیین پارامترهای مدل VG برای SWRC چهار بافت خاک کشاورزی در چین استفاده شدند. ضریب تعیین (R2) و خطای ریشه مربع میانگین (RMSE) برای تعیین تفاوت ها بین مقادیر پیش بینی شده و مقادیر اندازه گیری شده استفاده شدند. مقادیر R2 برای IPSO، GA و SA در برآورد پارامترهای معادله VG بزرگتر مساوی با 0.960 می باشند. مقادیر R2 و RMSE در تعیین پارامترهای مدل VG برای چهار بافت خاک توسط IPSO به ترتیب بالاترین و پایین ترین می باشند. این نشان داد که عملکرد بهینه سازی پارامتر IPSO بهتر از GA و SA است.
Abstract:
An improved particle swarm optimization (IPSO) was proposed and the intelligent algorithms such as IPSO, genetic algorithm (GA), and simulated annealing algorithm (SA) were introduced to determine parameters of Van Genuchten (VG) model for soil water retention curve (SWRC) of four typical agricultural soil textures (clay, clay loam, silt loam and sand loam) in China. For comparison, the SWRC in term of VG model was also fitted by a computer program RETC and pedotransfer function Rosetta, respectively. For four soil textures, the value of determination coefficient (R 2 ) and root mean square error (RMSE) in the estimation of VG equation parameters by IPSO are the highest and lowest in the above three intelligent algorithms, respectively. The simulated values of water content by IPSO are much closed to the measured values (R 2 = 0.990). It was found that the Rosetta is unable to estimate the SWRC adequately and the highest RMSE value is up to 1.096E − 01cm3 cm−3 . The predicted values of moisture content by Rosetta are far away from the measured values (R 2 = 0.585). The RETC provided good simulation results of water content (R 2 = 0.974). However, the soil residual water content (θr), of VG equation can not be obtained. It was concluded that the IPSO presented here is more reasonable and reliable to estimate the SWRC in term of VG model than the method of GA, SA, RETC and Rosetta.
1- Introduction
The soil water retention curve (SWRC), which is defined the relationship between soil water content and hydraulic potential, is an important physical property of soil material [1]. SWRC is indispensable when studying water flow processes and modelling water and solute movement through an unsaturated soil or when calculating the water availability for plants [2]. Empirical formulas are widely used to describe SWRC, where Van Genuchten (VG) equation is almost appropriate to all the soil textures [3]. However, four independent parameters need to be determined in VG equation, and the parameter fitting involves in the solution of nonlinear problems. Commonly-used least square method not only highly depends on the initial value of parameter, but also generates phenomena of algorithm termination and negative value.
Many researchers have been intended to solve these problems, which are mainly divided into the following 4 types.
(1) The optimization algorithms such as the nonlinear simplex method, Picard iterative approach, simplex evolutionary method and nonlinear damping least square were used to fit parameters of VG model [4, 5].
(2) The computer program, RETC [3], Data Processing System (DSP) and nonlinear function toolbox of MATLAB [6] were applied to estimate the VG equation parameters. However, the above approaches (1) and (2) strongly rely on the initial values of parameters. It is the same as the least square method.
6- Conclusions
An improved particle swarm optimization (IPSO) was presented in this study. The intelligent algorithms such as IPSO, GA, and SA were used to determine parameters of VG model for the SWRC of four agricultural soil samples in China. The coefficient of determination (R 2 ) and root mean square error (RMSE) were used to quantify the differences between the predicted values and the measured values. The R 2 values for IPSO, GA and SA in the estimation of VG equation parameters are equal or greater than 0.960. The R 2 and RMSE values in the determination of parameters of VG model for four soil textures by IPSO are the highest and lowest, respectively. It indicated that the performance of parameter-optimization of IPSO is better than GA and SA.
چکیده
1- مقدمه
2- مدل ون-گنوختن
3- اصل روش های عددی
1-3 الگوریتم ژنتیک
3-2 الگوریتم تبرید شبیه سازی شده
3-3 بهینه سازی ازدحام ذرات تعمیم یافته
4- مواد و روش ها
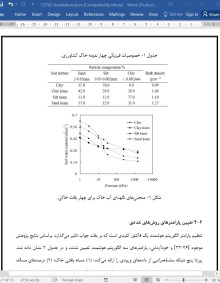
1-4 داده های خاک
4-2 تعیین پارامترهای روش های عددی
5- نتایج و بحث
5-1 عملکرد الگوریتم هوشمند برای برآورد پارامترهای مدل VG
5-2 مقایسه IPSO با RETC و روزتا
6- نتیجه گیری
منابع
Abstract
1 Introduction
2 Van Genuchten Model
3 Principle of numerical methods
3.1 Genetic algorithm
3.2 Simulated annealing algorithm
3.3 Improved particle swarm optimization
4 Materials and methods
4.1 Soil data
4.2 Parameters determination of numeric methods
5 Results and discussion
5.1 Performance of intelligent algorithm for estimating parameters of VG model
5.2 Comparison of IPSO with RETC and Rosetta
6 Conclusions
References
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه