
ماتریس های مشتق گیری در پایه های چند جمله ای
چکیده
ماتریس مشتقگیری صریح در چند پایه چند جملهای در این مقاله ارائه شده است. ایده این است که از هرگونه تغییر پایه در فرآیند مشتقگیری چند جملهای اجتناب کنیم. این مقاله هم دارای پایههای چند جملهای درجه - مدرج مانند پایههای متعامد، و هم دارای پایههای چند جملهای غیر مدج شامل پایههای لاگرانژ و برنشتاین است. در این مقاله، فرمولهای صریحی را برای ماتریس مشتقگیری D در پایههای چندجملهای مختلف به دست آوردهایم. مهمترین مزیت داشتنِ صریح D این است که هیچ نیاز به رفتن از پایهای به پایه دیگر (معمولا تک جملهای) برای مشتقگیری از یک چندجملهای در پایه ارائه شده نیست. علاوهبراین، با داشتن D میتوانیم به سادگی مشتقات مرتبه بالاتر یک چندجملهای را در پایه اصلی آن بیابیم. میتوان امیدوار بود که الگوریتمهای کارامدتر مربوط به چندجملهای، مانند روشهای ریشهیابی، را بتوان با استفاده از D توسعه داد. این نتایج را میتوان به سادگی به چندجملهایهای ماتریسی در پایههای مختلف توسعه داد.
Abstract
Explicit differentiation matrices in various polynomial bases are presented in this work. The idea is to avoid any change of basis in the process of polynomial differentiation. This article concerns both degree-graded polynomial bases such as orthogonal bases, and non-degree-graded polynomial bases including the Lagrange and Bernstein bases. In this paper, we have found explicit formulas for the differentiation matrix, D, in various polynomial bases. The most important advantage of having D explicitly is that there is no need to go from one basis to another (normally monomial) to differentiate a polynomial in a given basis. Moreover, having D, we can easily find higher order derivatives of any polynomial in its original basis. One may hope that new and more efficient polynomial-related algorithms, such as root-finding methods, can be developed using D. These results can be easily extended to matrix polynomials in different bases.
چکیده
مقدمه
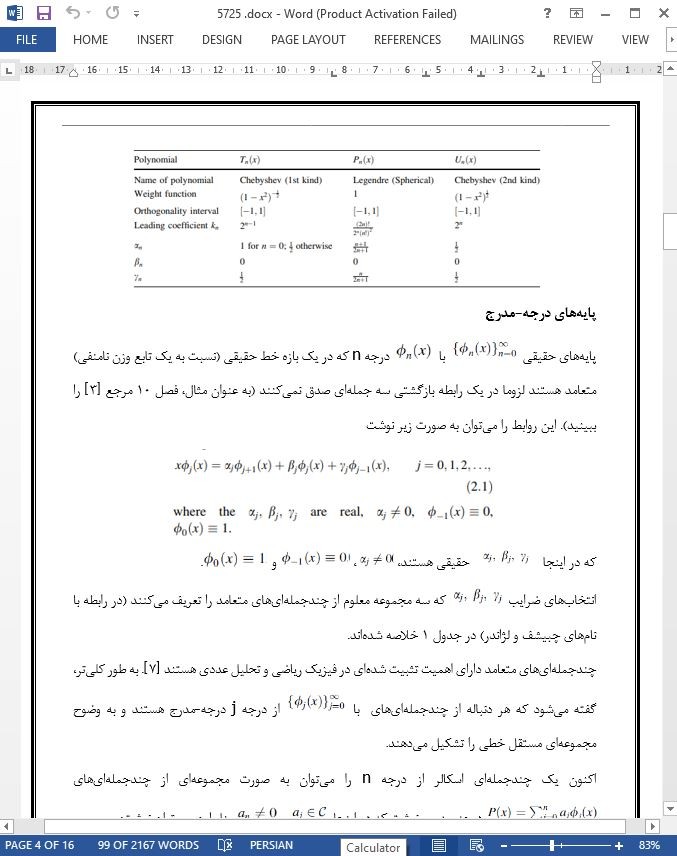
پایههای درجه-مدرج
پایههای درجه-مدرج ویژه
پایه برنشتاین
پایه لاگرانژ
نکات نتیجهگیری
Abstract
Introduction
Degree-graded bases
Special degree-graded bases
Bernstein basis
Lagrange basis
Concluding remarks
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه
