دانلود رایگان مقاله مسیرگزینی وسایل با بارگیری متقابل در زنجیره عرضه کالا

چکیده

     بارگیری متقابل روشی موثر برای کنترل جریان کالاهاست، که در مدیریت زنجیره عرضه حیاتی می‌باشد. در این مقاله، مدلی را در نظر می‌گیریم که بارگیری متقابل را با مساله مسیرگزینی وسایل اجماع خواهد نمود. در این مدل، مجموعه‌ای از وسایل مشابه برای انتقال اجناس از عمده فروشان به خرده فروشان با بارگیری متقابل مورد استفاده قرار گرفته است و تمام فرایند باید درون افق برنامه‌ریزی باشد. هر عمده فروش و خرده فروش فقط یکبار ملاقات می شود و مقدار کلی اجناس در یک وسیله باید از ظرفیت آن کمتر باشد. هدف مساله تعیین شمار وسایل و مجموعه ای از برنامه وسایل، با مجموع کمینه هزینه عملیاتی و انتقال است. یک الگوریتم جستجوی بازدارنده (TS) جدید به منظور دستیابی به یک راه حل امکانپذیر مناسب برای مساله پیشنهاد شده است. با آزمایشات محاسباتی گسترده، نشان داده شده است که الگوریتم TS پیشنهادی قابلیت دستیابی به بازدهی بهتری را نسبت به الگوریتم TS موجود دارد و زمان محاسباتی کمتری نیز دارد. برای اندازه مساله مختلف، بهبود میانگین بین 10-36% می‌باشد.

1. معرفی

     به طورکلی، فرایند تولید شامل خرید مواد خام از تولیدکنندگان، ساخت، انبارکردن و تحویل محصولات نهایی به مصرف کنندگان می باشد. سیستم شامل محصولات انتقالی یا خدمات تولیدکنندگان به مصرف کنندگان به زنجیره عرضه معروف است. به طور متداول، اعضای زنجیره عرضه نظیر عمده فروشان، سازندگان و مشتریان به دنبال بازدهی بالا و راحتی برای خود هستند، و معمولا بهبود جهانی یا بازدهی کلی را با عاملیت اعضای دیگر زنجیره عرضه در نظر نمی گیرند. درنتیجه، وقتی اعضای بالادست و پایین دست نمی توانند در زنجیره عرضه با یکدیگر تعامل کنند، هزینه بیشتری برای سیستم به وجود خواهد آمد. به منظور کاهش هزینه کلی در زنجیره عرضه، درنظرگرفتن تمامی اعضای زنجیره عرضه و استفاده از روش های موثر برای دستیابی به هزینه سیستمی کمتر واجب است. این تلاش به عنوان یک وظیفه ضروری در مدیریت زنجیره عرضه شناخته می شود و به طور رسمی به عنوان مجموعه روش های به کارگرفته شده برای اجتماع موثر عمده فروشان، سازندگان، انبارها و فروشگاه ها تعریف می شود. درنتیجه، محصولات قابلیت تولید و توزیع با مقادیر صحیح ، مکان صحیح و زمان صحیح را خواهند داشت که منتج به هزینه های سیستمی کمینه و ارضای نیازهای مشتریان خواهد شد (Simchi-Levi, Kaminsky,& Simchi-Levi, 2003).

     براساس قواعد حسابداری، دفتر کالاها می تواند بسته به جایی که در مراحل مختلف چرخه تولید وجود دارد، اسامی مختلفی داشته باشد. دفتر کالاها در انبار عمده فروشان می تواند مواد خام گفته شود. در فرایند تولید می تواند کار-در-فرایند (WIP) یا فهرست اموال در-فرایند گفته شود. علاوه براین، وقتی  کامل و برای مشتری فرستاده می شود کالای نهایی گفته خواهد شد. مواد خام، کار-در-فرایند و کالای نهایی همگی فهرست اموال هستند. یکی از مفاهیم اصلی مدیریت زنجیره عرضه، کنترل جریان فهرست اموال می باشد. 

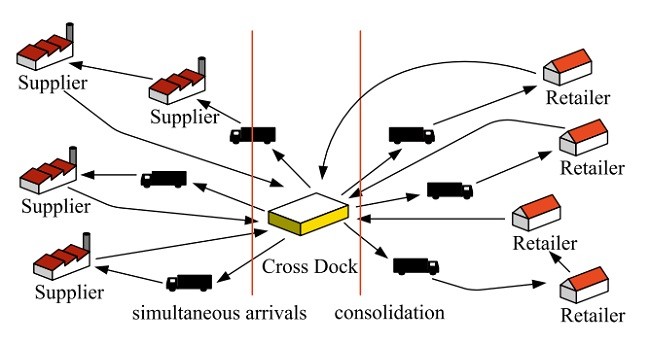
     یک روش انبارداری که بارگیری متقابل نامیده می شود، روشی مترقی برای کاهش فهرست اموال درکنار ارضای نیازهای مشتریان است. حین جهت دهی به جریان بین تغذیه کنندگان مواد خام و سازندگان، این روش می تواند به کاهش ذخیره اموال کمک کند. بارگیری متقابل مربوط به انتقال مستقیم کالاها از انبار اولیه تا انبار ارسال کالاهاست که کالاها برای مدت زمان کمی در حدود معمول 12 ساعت انبار می شوند یا مستقیما برای مشتریان فرستاده می شوند (Apte & Viswanathan, 2000;Kreng & Chen, 2008). روش بارگیری متقابل، درحالی که طی یک فرایند مستحکم امکان دسته بندی و بارگیری کالاها برای وسایل تحویل را می دهد، باعث حذف سهم عاملیت فهرست اموال در یک انبار سنتی می شود (Wen, Larsen,Clausen, Cordeau, & Laporte, 2008). مفهوم بارگیری متقابل در شکل 1 تشریح شده است که دو نقطه اساسی آن ورود و ادغام همزمان می باشد. اگر وسایل ناوگان برداشتن کالا نتوانند به طور همزمان به محل بارگیری متقابل برسند، فرایند ادغام تا زمانی تمام کالاها مجتمع شوند به تاخیر خواهد افتاد، و درنتیجه باعث افزایش زمان انتظار و سطح بارگیری در بارگیری متقابل خواهد شد.

     اکثر مطالعات روی بارگیری متقابل، بر مفهوم بارگیری متقابل، طراحی فیزیکی آن یا تعیین مکانی آن تکیه دارد. آپت و ویسواناتان (2000) ساختاری را برای طراحی یک سیستم بارگیری متقابل پیشنهاد نموده اند و خاطرنشان کرده اند که بارگیری متقابل می تواند به طور موثر باعث کاهش اساسی در هزینه انتقال بدون افزایش فهرست کالاها شود. سونگ و سانگ (2003) یک الگوریتم جستجوی بازدارنده را برای شبکه سرویس مجتمع، به منظور یافتن مکان بارگیری متقابل و وسایل نقلیه پیشنهاد نموده اند. آنان خاطرنشان کرده اند که استراتژی بارگیری متقابل به دلیل داشتن پتانسیل بالا برای کاهش هزینه انتقال و زمان تحویل بدون افزایش فهرست کالاها، مفید است. گوموس و بوکبیندر (2004) از یک نرم افزار تجاری شامل LINDO و CPLEX برای تعیین سیاست های انتقال در شبکه تدارکات و مکان های بهینه بارگیری متقابل استفاده کرده اند. بتازگی، کرنگ و چن (2008) دو روش ، یک مدل بارگیری متقابل و یک مدل انبارداری سنتی را، به منظور متناسب کردن تولید و توزیع برای کاهش هزینه های مربوطه در زنجیره عرضه توسعه داده اند. 

     از طرف دیگر، مساله کلاسیک مسیرگزینی وسایل (VRP)، شامل خدمت به مجموعه ای از مشتریان با تقاضاهای معلوم با ناوگان وسایل نقلیه از یک مرکز توزع واحد می باشد. هدف VRP کمینه کردن فاصله کلی و شمار وسایل نقلیه است که ماموریت خود را در انبار مرکزی آغاز و پایان می دهند. موشیوف (1998) گفته است که بسیاری از کاربردهای VRP ، شامل سرویس های برداشتن و تحویل کالا، مساله برداشتن و تحویل کالا (PDP) نامیده می شوند. در یک VRP ، ارضای نیازهای دو نوع خاص مشتریان الزامی است: مشتریان متقاضی و مشتریان عمده فروش. مشتریان متقاضی به یک محموله از یک انبار یا مشتریان عمده فروش دیگر نیاز دارند. مشتریان عمده فروش به حمل کالاها به بیرون نیاز دارند.هدف مساله یافتن ماموریت با کمترین طول مسافت برای یک وسیله بارگیری شده است که طول ماموریت از انباری با کالاهای کافی برای ارضای نیاز مشتریان شروع شده، در شبکه به منظور تحویل کالاها به مشتریان متقاضی حرکت کرده و کالاها را از مشتریان عمده فروش جمع آوری می کند (Tzoreff, Granot, Granot, & Sosic,2002). 

     همانطور که در بالا بحث شد، اگرچه مطالعات زیادی روی بارگیری متقابل و VRP وجود دارد، مقالات کمی موجود است که هردو مورد بارگیری متقابل و VRP را همزمان در نظر گرفته باشند. بکارگیری بارگیری متقابل در یک کار VRP بااهمیت است، زیرا این مساله در عمل خیلی متداول است. کار لی، ژونگ و لی (2006) احتمالا اولین کاری است که هردو مورد بارگیری متقابل و VRP را در نظر می گیرد. آنان یک جستجوی بازدارنده (TS) را برای تعیین شمار وسایل نقلیه و برنامه مسیرگزینی بهینه وسایل در بارگیری متقابل پیشنهاد نموده اند تا مجموع هزینه انتقال و هزینه ثابت وسایل نقلیه را کمینه نماید. در این مقاله، یک الگوریتم جستجوی بازدارنده (TS) جدید توسعه داده شده است و مقایسه بازدهی آن با کار لی و همکاران ارائه شده است.

     بقیه این مقاله به صورت زیر سازمان یافته است. تشریح مساله ر بخش 2 ارائه شده است. الگوریتم جستجوی بازدارنده (TS) پیشنهادی در بخش3 آمده است. بخش4 شامل تمام آزمایشات محاسباتی و بخش 5 شامل نتایج و بحث است.

2. تشریح مساله

     براساس بارباروسوگلو و ازگور (1999)، طرح حمل و نقل بهینه می تواند با زیربهینه سازی های چندگانه در مدیریت زنجیره عرضه جایگزین شود، زیرا مسایل نقلیه اختصاص یافته به یک مرکز توزیع مشخص، ناحیه گسترده ای را پوشش می دهند. بنابراین، یک شبکه توزیع با تنها یک محل بارگیری متقابل، در این مقاله در نظر گرفته شده است. مساله موردنظر در شکل2 تشریح شده است که فرض بر این است که تمام وسایل در محل بارگیری متقابل قرار دارند و تحویل جداگانه مجاز نیست. در شکل، یک مثلث مربوط به عمده فروش و چرخه منتهی به خرده فروش است. وسایل نقلیه برداشت کننده کالا از محل بارگیری متقابل شروع نموده و به طور همزمان به محل بارگیری منقابل می رسند. سپس وسایل تحویلی به سمت خرده فروشان می روند و پس از تکمیل ماموریت به محل بارگیری متقابل بازمی گردند. هدف مساله تعیین شمار وسایل نقلیه و بهترین مسیرگزینی، به گونه ای است که زمان حضور هر وسیله باعث کمینه کردن مجموع هزینه عملیاتی و انتقال شود.

     در این مقاله نمادهای زیر استفاده شده است:

 n : تعداد گره ها (عمده فروش ها یا خرده فروش ها) در شبکه نمادین.

m : تعداد وسایل دردسترس که همگی یکسان هستند.

Q : ظرفیت وسیله که برای تمام وسایل یکسان است.

pi : ظرفیت بارگیری در گره برداشت i.

di : ظرفیت تخلیه بار در گره تحویل i .

cij : هزینه انتقال از گره i به گره j .

tij : زمان انتقال بین گره i و گره j . .

ok : هزینه عملیاتی وسیله k .

T : مدت برنامه ریزی.

abstrac

     Cross-docking is considered as an efficient method to control the inventory flow, which is essential in supply chain management. In this paper, we consider a model that integrates cross-docking into the vehicle routing problem. In the model, a set of identical vehicles are used to transport goods from supplies to retailers through a cross-dock and the whole process must be completed in the planning horizon. Each supplier and retailer can be visited only once and the total quantity of goods in a vehicle must be less than its capacity. The objective of the problem is to determine the number of vehicles and a set of vehicle schedules with a minimum sum of operational cost and transportation cost. A new tabu search (TS) algorithm is proposed to obtain a good feasible solution for the problem. Through extensive computational experiments, it is shown that the proposed TS algorithm can achieve better performance than an existing TS algorithm while using much less computation time. The average improvements are as high as 10–36% for different size of problems.

1. Introduction

     In general, the production procedure consists of purchasing raw materials from suppliers, manufacturing, storing, and delivering end products to customers. The system involving moving products or services from suppliers to customers is referred to as a supply chain. Traditionally, members in a supply chain such as suppliers, manufacturers, and customers are looking for the highest efficiency simply for themselves, and typically do not consider global optimization or total efficiency by factoring in other members in the supply chain. Consequently, once the upstream and downstream sides cannot coordinate with each other in a supply chain, it will incur a higher system cost. In order to reduce the total cost in a supply chain, it is indispensable to consider all supply chain members at the same time and use more effective methods to achieve a lower system cost. This endeavor is considered an essential task of supply chain management and can be formally defined as a set of approaches utilized to efficiently integrate suppliers, manufacturers, warehouses, and stores. As a result, products can be produced and distributed at the right quantities, to the right location, and at the right time, which results in minimal systemwide costs while fulfilling customer demands (Simchi-Levi, Kaminsky, & Simchi-Levi, 2003).

     According to the principles of accounting, inventory can have different names depending on where it resides at the various stages of the production life cycle. Inventory can be seen as raw materials when it is stored in the supplier’s warehouse. It can be work-in-process (WIP) (or called in-process inventory) when the material is in the procedure of production. Furthermore, inventory can be finished goods when WIP is completed and dispatched to the customer. Raw materials, work-in-process, and finish goods are all inventory. One of the major concepts of supply chain management is to control the flow of inventory.

     A warehousing strategy, called cross-docking, is considered a viable method to reduce inventory while satisfying customers’ needs. Through streamlining the flow between the suppliers and manufacturers, this strategy can help diminish inventory storage. Cross-docking deals with movement of goods directly from the receiving dock to the shipping dock, where the goods are stored in a cross-dock for a short time, usually less than 12 h, or just directly dispatched to the customers (Apte & Viswanathan, 2000; Kreng & Chen, 2008). The cross-docking strategy essentially eliminates the inventory holding function of a traditional warehouse while still allowing products to be classified and loaded to the delivery vehicles through a consolidation process (Wen, Larsen, Clausen, Cordeau, & Laporte, 2008). The concept of cross-docking is depicted in Fig. 1 in which the two key points are simultaneous arrival and consolidation. If vehicles of the pickup fleet could not arrive at the cross-dock simultaneously, then the consolidation process would be delayed until all goods are collected, and thereby increasing the waiting time and the inventory level at the crossdocking.

     Most studies on cross-docking discuss the concept of crossdocking, its physical design, or location determination. Apte and Viswanathan (2000) proposed a framework for designing a crossdocking system and indicated that cross-docking can effectively bring substantial reduction in the transportation cost without increasing inventory. Sung and Song (2003) proposed a tabu search algorithm for an integrated service network to find the locations of both cross-docks and vehicles. They pointed out that the crossdocking strategy has been acknowledged as having great potential to reduce transportation cost and delivery time without increasing inventory. Gumus and Bookbinder (2004) used commercial software including LINDO and CPLEX to determine transportation policies in a logistic network and optimal locations of cross-docks. Recently, Kreng and Chen (2008) developed two models, a crossdocking model and a traditional warehousing model, to coordinate both production and distribution in order to reduce relevant costs in a supply chain.

     On the other hand, the classic vehicle routing problem (VRP) involves the service of a set of customers with known demands by a fleet of vehicles from a single distribution center. The objective of the VRP is to minimize the total distance and the number of vehicles which start and end their tours at the central depot. Mosheiov (1998) stated that many applications of VRP involving pickup and delivery services are referred to the pickup and delivery problem (PDP). In a PDP, it is necessary to meet the needs of two special kinds of customers: demand customers and supply customers. For the demand customers, they need a shipment from a depot or other supply customers. For the supply customers, they need a shipment to take the goods away. The objective of the problem is to find a minimum length tour for a capacitated vehicle where the length tour starts at a depot loaded with enough goods to satisfy the customers, travels in the network to deliver the goods to the demand customers, and collects the goods from the supply customers (Tzoreff, Granot, Granot, & Sosic, 2002).

     As discussed above, although there exist many studies on cross-docking and VRP, there are few papers that consider both cross-docking and VRP simultaneously. Dealing with a VRP task with cross-docking is important because the problem is quite common in practice. The work of Lee, Jung, and Lee (2006) is probably the first that takes both VRP and cross-docking into consideration. They proposed a tabu search (TS) to determine the number of vehicles and the optimal vehicle routing schedule at a cross-dock to minimize the sum of transportation cost and fixed cost of vehicles. In this paper, a new tabu search (TS) algorithm is developed and a comparison of its performance with Lee et al.’s TS is presented.

     The remaining of this paper is organized as follows. The problem description is presented in Section 2. The proposed TS algorithm is given in Section 3. Section 4 contains all computational experiments, followed by the conclusions in Section 5.

2. Problem description

     According to Barbarosoglu and Ozgur (1999), optimal transportation planning can be replaced by multiple sub-optimizations in supply chain management because vehicles allocated to a certain distribution center take charge of an exclusive area. Thus, a distribution network with only a cross-dock is considered in this paper. The considered problem is described by Fig. 2, where it is assumed that all the vehicles are located in the cross-dock and split deliveries are not allowed. In the figure, a triangle represents a supplier and a cycle represents a retailer. The pickup vehicles start from the cross-dock and arrive at the cross-dock simultaneously. Then, the delivery vehicles move to the retailers and return to the cross-dock after completing their tours. The objective of the problem is to determine the number of vehicles and the best route as well as the arrival time of each vehicle so as to minimize the sum of the operational cost of vehicles and the transportation cost.

     The following notation is used throughout the paper:

n number of nodes (suppliers or retailers) in the logistic network

m number of available vehicles, which are all identical

Q capacity of the vehicle, which is common to all vehicles

pi loading quantity in the pickup node i

di unloading quantity in the delivery node i

cij transportation cost from node i to node j tij travel time between node i and node j ok operational cost of vehicle k T planning horizon.

چکیده

1. معرفی

2. تشریح مساله

3. روش جستجوی بازدارنده

3. 1. طرح حل اولیه

3. 2. الگوریتم TS پیشنهادی

4. آزمایشات محاسباتی 

5. نتیجه و بحث

abstrac

1. Introduction

2. Problem description

3. The tabu search approach

3.1. Initial solution scheme

3.2. Proposed TS algorithm

4. Computational experiments

5. Conclusions

References