دانلود مقاله رمزنگاری مبتنی بر ویژگی مقاوم در برابر ورودی کمکی
چکیده
مدل ورودی کمکی کلاسی از خانواده توابع وارونناپذیر با نام F را برای شبیهسازی کلاسی بزرگ از نشت تعریف میکند. چنین تابعی به شکل f ∈ F به لحاظ نظریه اطلاعات میتواند کل کلید رمز SK را آشکار کند ولی از نظر محاسباتی همچنان بازیابی SK از f(SK) نشدنی است. این موضوع بدان معنا است که میتوان از SK برای چندین وظیفه استفاده کرد زیرا لازم نیست که SK به شکلی پیوسته نوسازی شود. ما نخستین طرح CP-ABE مبتنی بر طرحهای تسهیم راز خطی را پیشنهاد میکنیم که میتواند نشت بر روی کلید اصلی و نشت بر کلیدهای رمز مبتنی بر ویژگی با ورودیهای کمکی (AI) را تحمل کند. برای اثبات امنیت طرح ما، سه فرض اصلاح شده را در گروههای دوسویه مرتبه ترکیبی ارائه میکنیم و سختی آنها را اثبات میکنیم. تحت این فرضهای اصلاح شده، طرح ما میتواند از نظر ایمنی AI-CPA در مدل استاندارد اثبات شود. در نهایت، طرح ABE سیاست کلیدی را درست میکنیم که در برابر ورودیهای کمکی نیز مقاوم است.
1. مقدمه
با توسعه رایانش ابری ، کاربران تمایل به ذخیرهسازی دادههای خود بر روی سرورهای ابری دارند. توزیع این دادههای رمزنگاری شده به مجموعهای مشخص از کاربران در سیستمهای رمزنگاری سنتی ناکارآ است که از جمله این سیستمها میتوان به سیستم رمزنگاری مبتنی بر شناسه و PKI اشاره کرد علت این ناکارآمدی هم این است که اندازه متن رمزنگاری شده و هزینه محاسباتی الگوریتمهای رمزگشایی یا رمزگذاری با تعداد گیرندههای آن به شکل خطی در ارتباط هستند. به همین علت نخستین بار ساهای و واترز [1] مفهوم رمزنگاری مبتنی بر ویژگی را ارائه دادند. در رمزنگاری مبتنی بر ویژگی، متون رمزنگاری شده و کلیدها با مجموعهای از ویژگیها و ساختارهای دسترسی بر روی ویژگیها در ارتباط هستند. تنها زمانی که ویژگیهای متن رمزنگاری شده مطابق با کلید کاربر است، متن رمزنگاری شده مرتبط را میتوان رمزگشایی کرد. دو نوع از سیستمهای ABE وجود دارند: نخستین مورد سیاست متن رمزنگاری شده ABE یا به اختصار CP-ABE که در آن متنون رمزنگاری شده با ساختارهای دسترسی مرتبط هستند و کلیدها با مجموعهای از ویژگیها مرتبط هستند و مورد دوم سیاست کلیدی ABE یا به اختصار KP-ABE است که در آن کلیدها با ساختارهای دسترسی مرتبط هستند و متون رمزنگاری شده با مجموعهای از ویژگیها مرتبط هستند.
نحوه دستیابی به یک سیاست دسترسی رساتر بر روی بسیاری از ویژگیها مسئلهای مهم در ABE است. طرح ساهای و واترز محدود به آستانه خاصی از سیاستهای دسترسی با یک گیت آستانه بوده است. پس از آن لوکو و همکاران [15] از برنامههای پوشای یکنواخت (MPSها) به عنوان ساختار دسترسی برای طراحی یک CP-ABE و یک KP-ABE استفاده کردند که این موارد در گروههای دوسویه ترکیبی از نظر امنیتی اثبات شده بودند. با این حال، طرحهای آنها بسیار ناکارآمد هستند، زیرا طول متون و کلیدهای رمزنگاری و تعداد جفتها در رمزگشایی همه چندجملهایها در اندازه MSPs هستند. به منظور بهبود کارایی، برخی از سیستم های ABE از طرح تسهیم راز خطی (LSSS) یا فرمولهای بولی به عنوان ساختار دسترسی استفاده کردند. واترز از ماتریس LSSS به عنوان ساختار دسترسی برای پیادهسازی CP-ABE تحت فرضیات رمزنگاری غیرتعاملی استفاده کرد. در [6]، گویال و همکاران نقشهبرداری از یک درخت دسترسی جهانی را برای فرمولهسازی شامل گیتهای آستانه استفاده کردند. آنها از این تکنیک برای ساخت یک برنامه محدود CP-ABE استفاده کردند. ارتباط نزدیکی بین LSSS و ساختار دسترسی MSP وجود دارد. بیمل و همکاران [7] ثابت کردند که وجود LSSS برای یک ساختار دسترسی ویژه MSP معادل کوچکترین MSP است. پاندیت و همکاران [8] از مجموعههای کمینه برای تحقق بخشی به کوچکترین MSP برای توصیف ساختار دسترسی عمومی در سیستم ABE استفاده کردند. به تازگی، ژانگ و همکاران [12] یک CP-ABE و یک KP-ABE مقاوم در برابر نشت مستمر را با مجموعههای کمینه پیشنهاد دادند.
7. نتیجهگیری
در این مقاله، ما یک مدل امنیتی از CP-ABE مقاوم در برابر نشت نسبت به ورودی کمکی را ارائه دادیم و ساختاری منسجم بر اساس طرحهای تسهیم رازی خطی را ارائه دادیم. طرح ما میتواند در برابر نشت کلید اصلی و کلید رمز مبتنی بر ویژگی با ورودی کمکی تاب آورد. برای اثبات امنیتی طرح ما ما سه فرضیه استاتیک اصلاح شده را در گروههای دو سویه با مرتبه ترکیبی ارائه دادیم و تک تک آنها را با ذکر جزئیات اثبات کردیم. طرح ما همچنین اگر در مرحله راهاندازی اجازه وقوع نشت را ندهد به آسانی قادر به گسترش به یک طرح ABE مقاوم در برابر نشت کمکی مداوم است. در نهایت، ما همچنین یک طرح KP-ABE مقاوم در برابر ورودی کمکی را پیشنهاد دادیم.
Abstract
The auxiliary input model defines a class of computationally uninvertible function families F to simulate a large class of leakage. Such a function f ∈ F can information-theoretically reveal the entire secret key SK, but it is still computationally infeasible to recover SK from f(SK). That means SK can be used for multiple tasks, since SK doesn’t need to be continually refreshed. We propose the first CP-ABE scheme based on linear secret sharing schemes, that can tolerate leakage on master key and attribute-based secret keys with auxiliary input(AI). For the security proof of our scheme, we present three modified assumptions in composite order bilinear groups, and prove their hardness. Under these modified assumptions, our scheme can be proved AI-CPA secure in the standard model. Finally, we devise a key-policy ABE scheme also resilient to auxiliary input.
1 Introduction
With the development of cloud computing, there is a trend for users to store their data on the cloud server. It is inefficient to distribute these encrypted data to a specific set of users in traditional cryptosystems, e.g., PKI, ID-based cryptosystem, since the cipher-text size and computational cost of encryption/decryption algorithms are linear with the number of receivers. For this reason, Sahai and Waters [1] firstly proposed the concept of attribute-based encryption. In attribute-based encryption, cipher-texts and keys are associated with sets of attributes and access structure over attributes. Only when the attributes of the cipher-text match those of the users’ key, the corresponding cipher-text can be decrypted. There are two kinds of ABE systems: The first one is ciphertext-policy ABE (CP-ABE), where cipher-texts are associated with access structures and keys are associated with sets of attributes; the second one is key-policy ABE (KP-ABE), where keys are associated with access structure and cipher-texts are associated with sets of attributes.
How to achieve a more expressive access policy over many attributes is an important problem in ABE. Sahai and Waters’s [1] scheme was limited to specify as threshold access policies with one threshold gate. After then, Lewko et al. [5] used monotone span programs (MSPs) as access structure to devise a CP-ABE and a KP-ABE, which are proved secure in composite bilinear groups. However, their schemes are very inefficient, since the length of cipher-texts and keys, and the number of pairings in decryption are all polynomial in the size of MSPs. In order to improve the efficiency, some ABE systems make use of linear secret sharing scheme (LSSS) or boolean formulas as access structure. Waters [10] employed LSSS matrix as access structure to realize CP-ABE under concrete and noninteractive cryptographic assumptions. In [6], Goyal et al. provided a mapping from a universal access tree to formulas consisting of threshold gates. They used this technique to construct a bounded CP-ABE scheme. There is a close relation between LSSS and MSP access structure. Beimel et al. [7] proved that the existence of a LSSS for a specific MSP access structure is equivalent to a smallest MSP. Pandit et al. [8] used minimal sets to realize the smallest MSP for describing general access structure in ABE systems. Recently, Zhang et al. [12] proposed a CP-ABE and a KP-ABE resilient to continual leakage by minimal sets.
7 Conclusions
In this paper, we propose a security model of CP-ABE leakage resilient to auxiliary input, and a concrete construction based on linear secret sharing schemes. Our scheme can tolerate leakage on master key and attribute-based secret key with auxiliary input. For the security proof of our scheme, we present three modified static assumptions in composite order bilinear groups, and prove them in detail. Our scheme also can be easily extended to an ABE scheme resilient to continual auxiliary leakage, if it doesn’t allow leakage in setup phase. Finally, we also propose a KP-ABE scheme resilient to auxiliary input.
چکیده
1. مقدمه
2. پیشزمینه
2.1 فرضیات سختی
2. 2 ساختار دسترسی و طرح تسهیم راز خطی
3 رمزنگاری مبتنی بر ویژگی با ورودی های کمکی
3.1 مدل امنیتی AI-CP-ABE
4. ساخت CP-ABE مقاوم در برابر مدل ورودی کمکی
1 .4 آمادهسازی
2. 4 ساخت و ساز
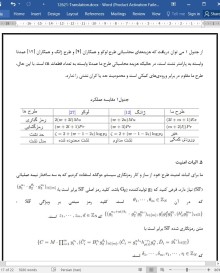
3 .4 مقایسه عملکرد
5. اثبات امنیت
6. KP-ABE مقاوم در برابر ورود کمکی
7. نتیجهگیری
منابع
Abstract
1 Introduction
2 Background
2.1 Hardness Assumptions
2.2 Access Structure and Linear Secret Sharing Scheme
3 Attribute Based Encryption with Auxiliary Inputs
3.1 Security Model of AI-CP-ABE
4 Construction of CP-ABE Resilient to Auxiliary Input Model
4.1 Preparation
4.2 Construction
4.3 Performance Comparison
5 Security Proof
6 KP-ABE Resilient to Auxiliary Input
7 Conclusions
References
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه