دانلود مقاله FL-MTSP : رویکرد منطق فازی جهت حل مساله چند فروشنده دوره گرده
چکیده
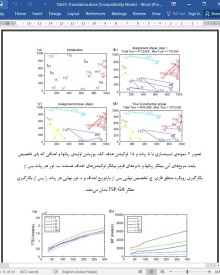
این مقاله به بررسی مسالهی تخصیص لوکیشنهای هدف -که قرار است بازدید شوند-، به رباتهای سیار میپردازد. ما این مساله را بصورت مسالهی چند فروشندهی دورهگردِ چندایستگاهیMD-MTSP تدوین میکنیم، یعنی یک نمونه مسالهی NP-Hard از MTSP. برخلاف اکثر آثار پژوهشیِ پیشین، ما به دنبال بهینهسازی معیارهای عملکرد هستیم، یعنی بیشینه مسافت طیشده و کل مسافت طیشده بطور همزمان. به منظور پرداختن به این مساله، ما FL-MTSP را مطرح میسازیم که یک رویکرد منطق فازیِ جدید است که هر دو معیار را در یک معیار فازیِ واحد ترکیب میکند، و مساله را به یک مسالهی بهینهسازیِ هدفِ واحد فرو میکاهد. شبیهسازیهای گسترده حاکی از این هستند که رویکرد منطق فازیِ پیشنهادیِ ما، از نظر ارائهی بدهبستانی مطلوب از دو معیار عملکردیِ مورد نظر، عملکرد بهتری نسبت به یک الگوریتم عامِ تعمیمیافته دارد. بعلاوه، روشن شد که زمان اجرای FL-MTSP همیشه سریعتر از رویکرد MDMTSP_GA بود و عدد 89 درصد را نشان میداد.
1. مقدمه
در اپلیکیشنهای رباتیک پیچیده مانند تریگویی (2012)، کوبا (2012)، خمیس (2011، پیپین (2013) و فضلی (2010)، رباتها معمولاً باید با یکدیگر همکاری کنند تا ماموریت خویش را به نحوی کارآمد به انجام رسانند. در واقع، سیستمهای رباتهای همکار، برای مصارف زیادی، جایگزینی توصیهشده را برای سیستمهای تکرباتی معرفی میکنند و تاثیر همکاری بین رباتها را که به انجام بهترِ ماموریتشان میانجامد، مدنظر قرار میدهند که به انجام بهتر ماموریتشان میانجامد. مساله تخصیص وظیفهی چندرباتی (MRTA)، به تخصیص وظایف به رباتها جهت انجام ماموریتهای مشارکتی میپردازد. مساله MRTA را میتوان این گونه تدوین کرد: با فرض اینکه n ربات و m وظیفه داشته باشیم، هدف عبارت میشود از انجام کارآمد وظایفِ مورد نظر به منظور کمینهسازی کل هزینهی سیستم. در متون پژوهشی، مقالات زیادی به ارائهی راهحلهایی برای مساله MRTA پرداختهاند و آن را در کانتکستهای مختلفی بکار بردهاند. تحلیل رسمی و تاکسونومیِ مسائل تخصیص وظیفهی چندرباتی در حوزههای مختلف، در مقاله تیگویی (2014) ارائه شده است. این مقاله، سه مقولهی اصلی را تعریف میکند: 1) رباتهای تکوظیفهای (ST) در مقابل رباتهای چند وظیفهای (MT)، 2) وظایف تکرباتی (SR) در مقابل وظایف چندرباتی (MR) و 3) وظیفهی فوری (IA) در مقابل وظیفهی طولانی (TA). بر اساس این تاکسونومی، رویکرد پیشنهادی ما به مقولهی ST , SR, TA تعلق دارد.
در متون پژوهشی، رویکردهای موجود را میتوان به دو مقوله تقسیم کرد: 1) رویکرد متمرکز: دانش اطلاعات جهانی را توسط یک عامل مرکزی میآموزد (مثلاً ایستگاه کنترل)، که قادر است راهحلی شِبهبهینه را برای مسالهی مربوطه، محاسبه کند، 2) رویکرد توزیعشده: تصمیمات (یا راهحلهای محلی) بر مبنای اطلاعات محلی برای هر عاملی است که وظیفهای را انجام میدهند (مثلاً ربات).
6. نتیجه
مسالهی چندین فروشندهی دورهگردِ چندنقطهای، یک حوزهی پژوهشی است که در اپلیکیشنهای رباتیک متعددی بکار رفته است که در آنها فروشنده از فضای کار یکسانی برخوردار است. به منظور حل کردنِ MD-MTSP، این مقاله یک راهحل متمرکز مبتنی بر استفاده از منطق فازی مطرح کرده است تا دو هدف را با هم ادغام کند: هدف کمینهسازی کل مسافت طیشده توسط فروشندگان و هدف کمینهسازی بیشینه مسافت طیشده توسط ربات. این رویکرد از دو فاز تشکیل شده است: فاز تخصیص که در آنها تخصیص اهداف بر مبنای خروجی سیستم منطق فازی است، و فاز ساخت تور که در آن ما از الگوریتم ژنتیک موجود به منظور ایجاد یک تور فروبَهین برای هر ربات استفاده میکنیم. رویکرد ما با یک حلگر MD-MTSP بر مبنای الگوریتم ژنتیک مقایسه میشود. رویکرد ما، هم در زمینه اهداف و هم بلحاظ زمان اجرا، عملکرد بهتری نسبت به رویکرد GA دارد. ما راهحل خودمان را با دو الگوریتم تکهدفه مقایسه کردیم. ثابت کردیم که الگوریتم چندهدفهی ما، بدهبستانی بین کل مسافت طیشده و بیشینه مسافت طیشده فراهم میسازد.
Abstract
This paper considers the problem of assigning target locations to be visited by mobile robots. We formulate the problem as a multiple-depot multiple traveling salesman problem (MD-MTSP), an NP-Hard problem instance of the MTSP. In contrast to most previous works, we seek to optimize multiple performance criteria, namely the maximum traveled distance and the total traveled distance, simultaneously. To address this problem, we propose, FL-MTSP, a new fuzzy logic approach that combines both metrics into a single fuzzy metric, reducing the problem to a singleobjective optimization problem. Extensive simulations show that the proposed fuzzy logic approach outperforms an existing centralized Genetic Algorithm (MDMTSP_GA) in terms of providing a good trade-off of the two performance metrics of interest. In addition, the execution time of FL-MTSP was shown to be always faster than that of the MDMTSP_GA approach, with a ratio of 89%.
1 Introduction
In complex robotics applications, such as Trigui et al. (2012), Koubâa et al. (2012), Khamis et al. (2011), Pippin et al. (2013), and Fazli et al.(2010), robots typically need to collaborate together in order to complete their mission efficiently. In fact, cooperative robots systems represent a recommended alternative to single-robot systems for a vast array of applications, considering the collaborative effect between robots that leads to accomplishing their missions more efficiently. The multi-robot task allocation problem (MRTA) deals with assigning tasks to robots to perform collaborative missions. The MRTA problem can be formulated as follows: given n robots and m tasks, the objective consists of ensuring an efficient assignment of the tasks under consideration in order to minimize the overall system cost. In the literature, several works have proposed different solutions to the MRTA problem and applied it in different contexts. A formal analysis and taxonomy of multi-robot task allocation problems in several fields is given in Trigui et al. (2014). The paper defines three main categories: (1) single-task robots (ST) versus multi-task robots (MT), (2) single-robot tasks (SR) versus multi-robot tasks (MR), and (3) instantaneous assignment (IA) versus time-extended assignment (TA). According to this taxonomy, our proposed approach belongs to the category of (ST, SR, TA).
In the literature, existing approaches can be divided into two categories, namely: (1) the centralized approach: it assumes the knowledge of global information by a central agent (e.g., control station), which is able to calculate a nearoptimal solution to the allocation problem, (2) the distributed approach: decisions (or local solutions) are based on local information for each agent performing the task (e.g., robot).
6 Conclusion
Multiple-depot multiple traveling salesman problem is an interesting research area applied in several robotic applications where salesmen share the same workspace. To solve the MD-MTSP, the paper proposed a centralized solution based on the use of the fuzzy logic algebra to combine two objectives: the objective of minimizing the total traveled distance by all the salesmen and the objective of minimizing the maximum traveled distance by any robot. The approach consists of two phases: The assignment phase where the targets allocation is based on the output of the fuzzy logic system, and the tour construction phase, where we used an existing genetic algorithm to build a sub-optimal tour for each robot. Our approach is compared against an existing MDMTSP solver based on the genetic algorithm. Our approach outperformed the GA approach on both the objectives and also in terms of execution time. We compared our solution against two single-objective algorithms. We proved that our multi-objective algorithm provides a trade-off between total traveled distance and the maximum traveled distance.
چکیده
1. مقدمه
2. آثار مرتبط
3. تدوین مساله
4. راهحل پیشنهادی
4.1 طراحی قواعد منطق فازی
4.2 طراحیِ الگوریتم
4.2.1 فاز ارزیابی (الگوریتم 2)
4.2.2 فاز ایجاد تور (الگوریتم 3)
5. ارزیابی عملکرد
6. نتیجه
منابع
Abstract
1 Introduction
2 Related works
3 Problem formulation
4 Proposed solution
4.1 Fuzzy logic rules design
4.2 Algorithm design
4.2.1 Assignment phase (Algorithm 2)
4.2.2 Tour construction phase (Algorithm 3)
5 Performance evaluation
6 Conclusion
References
- اصل مقاله انگلیسی با فرمت ورد (word) با قابلیت ویرایش
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه