دانلود مقاله بهینه سازی چندهدفه با استفاده از الگوریتم های تکاملی

چکیده 
     از سال 1985  چند روش تکاملی برای بهینه‌سازی چندهدفه توسعه یافته است که قادر به یافتن چند راه‌حل در یک دور اجرا (run) هستند. با این حال، اکثر مطالعاتِ مقایسه‌ای که در دسترس هستند، به صورت کیفی بوده و محدود به دو روش اصلی می‌شوند. در این مقاله یک مقایسه گسترده و کمّی عرضه شده است که از 4 الگوریتم‌ تکاملی چندهدفه برای مسئله 1/0 کوله‌پشتی (knapsack problem) استفاده می‌کند. 

1-مقدمه 
     بسیاری از مسائل دنیای واقعی نیازمند بهینه‌سازی همزمان چند هدف قابل‌اندازه‌گیری و اغلب رقابتی است. معمولاً هیچ راه‌حل منفردی وجود ندارد بلکه مجموعه‌ای از راه‌حل‌های جایگزین در کار است. از نگاه کلی‌تر، این راه‌حل‌ها به گونه‌ای بهینه هستند که اگر همه اهداف (objectives) را در نظر بگیریم، در فضای جستجو هیچ راه‌حلی نسبت به دیگری برتری ندارد. به این راه‌حل‌ها، راه‌حل‌های بهینه‌شده پارِتو گفته می‌شود. 
2- الگوریتم‌های تکاملی چندهدفه 
     مروری جامع بر الگوریتم‌های تکاملی در بهینه‌سازی چندهدفه در مقاله‌ای از فونسکا و فلمینگ صورت گرفته‌ است. نویسندگان این مقاله چند روش تکاملی را بررسی کرده‌اند که شامل روش‌های انباشت ساده، روش‌های جمعیتی غیرپارتو و روش‌های مبتنی بر پارتو می‌شود. همچنین روش‌های استفاده از القای همسایگی (niche) نیز آورده شده‌اند. 
     روش‌های انباشتی به ترکیب‌کردن اهداف درون یک تابع نردبانی بالاتر مشغول‌اند که برای محاسبات شایستگی (fitness) از آنها استفاده می‌شود. این روش‌ها یک راه‌حل منفرد (single) فراهم می‌آورند و نیازمند داشتن دانش عمیقی هستند که معمولاً دردسترس نیست. روش‌های جمعیتی غیرپارتو قادر هستند تا راه‌حل‌های غیرمغلوبی را به صورت موازی پیدا کرده و بنابراین جمعیت اساساً برای راه‌حل‌های غیرمغلوب کنترل می‌شود. اما برعکس روش‌های پارتو، روش‌های جمعیتی غیرپارتو از مفهومِ غلبه (dominance) پارتو به طور مستقیم استفاده نمی‌کنند. الگوریتم‌های تکاملی پارتو، راه‌حل‌ها را بر اساس رابطه > مقایسه می‌کنند تا احتمالِ تولیدمثل هر فرد را محاسبه کنند. اولین بار این نوع مسئله شایستگی را گلدبرگ پیشنهاد داد. 
 5- نتیجه‌گیری و چشم‌انداز آتی 
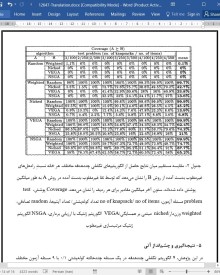
     در این پژوهش، 4 الگوریتم تکاملی چندهدفه در یک مسئله چندحالته کوله‌پشتی 1/0 با 9 مسئله آزمون مختلف مقایسه شدند. کیفیت مجموعه‌های پارتو بهینه‌شده به صورت کمّی با معیار اندازه فضای پوشش‌داده شده سنجیده شد. علاوه بر این، روش‌ها به طور مستقیم از طریق ارزیابی نتایج با توجه به مفهوم غلبه پارتو (pareto dominance) مقایسه شدند. 
     همه الگوریتم‌های تکاملی نسبت به راهبرد جستجوی صرفاً تصادفی، عملکرد بهتری داشتند. روش جستجوی صرفاً تصادفی نقاط جدیدی را به صورت تصادفی در فضای کاوش تولید می‌کند بدون اینکه شباهت‌های میان راه‌حل‌ها را در نظر بگیرد. از میان همه الگوریتم‌های تکاملی، الگوریتم ژنتیک مرتب سازی غیرمغلوب که توسط سرینیواس و دب پیشنهاد شده است، بهترین ارزیابی را در مورد مسائل آزمون از خود نشان داد. در رتبه دوم، الگوریتم ژنتیک با ارزیابی برداری قرار گرفت. در مورد دو روش دیگر، نتایج مبهم هستند. در مورد مسئله دو هدفه، الگوریتم ژنتیک پارتو مبتنی بر همسایگی که توسط هرن و نافپلیوتیس ارائه شده است، بهتر از روش وزن‌دار مجموع عمل کرد. از سوی دیگر الگوریتم تکاملی وزن‌دار مجموع که توسط هاجلا و لین پیشنهاد شده، ارزیابی بهتری در مسائل سه هدفه داشت. در مورد مسائل 4 هدفه هیچ از دو الگوریتم مزیتی بر دیگری نداشت. 
     از نقطه نظر چشم‌انداز آتی، موضوع توزیع‌کردن جمعیت روی سطح بده‌بستان (trade-off) بهتر است مورد مطالعه بیشتری قرار بگیرد. در بسیاری از موارد جایی که سطح بده‌بستان پیوسته است یا شامل تعداد زیادی راه‌حل می‌شود، ضروری است که الگوریتم تکاملی قادر به انتخاب‌کردن راه‌حل‌های نماینده (representative) باشد. علاوه بر این، تاثیر محدودیت‌های جفت‌گیری نیز بهتر است بررسی شوند. اگرچه محدودیت‌های جفت‌گیری در موضوع الگوریتم‌های تکاملی چندهدفه چندان گسترده نیستند. در نهایت همانطور که مرجع (1) ابراز داشته است، داشتن نظریه‌ای برای بهینه‌سازی چندهدفه تکاملی نیازمند آزمون کردن روش‌های تخصیص شایستگی مختلف در ترکیب با طرح‌های انتخاب متفاوت است.

Abstract

     Since 1985 various evolutionary approaches to multiobjective optimization have been developed, capable of searching for multiple solutions concurrently in a single run. But the few comparative studies of different methods available to date are mostly qualitative and restricted to two approaches. In this paper an extensive, quantitative comparison is presented, applying four multiobjective evolutionary algorithms to an extended ~0/1 knapsack problem.

1 Introduction

     Many real-world problems involve simultaneous optimization of several incommensurable and often competing objectives. Usually, there is no single optimal solution, but rather a set of alternative solutions. These solutions are optimal in the wider sense that no other solutions in the search space are superior to them when all objectives are considered. They are known as Pareto-optimal solutions.

2 Multiobjective Evolutionary Algorithms

     A comprehensive overview of EAs in multiobjective optimization was published by Fonseca and Fleming [1]. The authors categorized several evolutionary approaches regarding plain aggregating approaches, population-based non-Pareto approaches and Pareto-based approaches; moreover, approaches using niche induction techniques were considered.

     Aggregation methods combine the objectives into a higher scalar function which is used for fitness calculation; they produce one single solution and require profound domain knowledge which is often not available. Population-based nonPareto approaches, however, are able to evolve multiple nondominated solutions in parallel; thereby, the population is mostly monitored for nondominated solutions. But in contrast to the Pareto-based approaches they do not make direct use of the concept of Pareto dominance. Pareto-based EAs compare solutions according to the ~- relation in order to determine the reproduction probability of each individual; this kind of fitness assignment was first proposed by Goldberg [3].

5 Conclusions and Future

     Work In this study we compared four multiobjective EA on a multiobjective 0/1 knapsack problem with nine different problem settings. The quality of the Paretooptimal sets achieved was measured quantitatively by the size of the space covered. Additionally, the approaches were compared directly by evaluating the outcomes regarding the concept of Pareto dominance.

     All EAs clearly outperformed a pure random search strategy which randomly generates new points in the search space without exploiting similarities between solutions. Among the EAs the Nondominated Sorting Genetic Algorithm (NSGA) proposed by Srinivas and Deb [11] achieved the best evaluations on all test problems, followed by Schaffer's VEGA [10] when all nine test problems are considered. Concerning the other two approaches, the results are ambiguous: In the two-objective case, the Niched Pareto Genetic Algorithm presented by Horn and Nafpliotis [5] outperformed the weighted-sum based approach proposed by Hajela and Lin [4]. On the other side, the latter EA achieved better evaluations for three objectives. In the case of four objectives neither of them was superior.

     Regarding future perspectives, the issue of distributing the population over the tradeoff surface might be subject to further examinations. In many applications, where the tradeoff surface is continuous or containing a huge number of solutions, it is essential that the EA is capable of "selecting" representative solutions. Furthermore, the influence of mating restrictions might be investigated, although restricted mating is not very widespread in the field of multiobjective EA. Finally, as stated in [1] a theory of evolutionary multiobjective optimization is much needed, examining different fitness assignment methods in combination with different selections schemes.

(جهت بزرگ نمایی روی عکس کلیک نمایید)

چکیده 
1-مقدمه 
2- الگوریتم‌های تکاملی چندهدفه 
2-1 الگوریتم ژنتیک با ارزیابی برداری            
2-2 انباشتن به وسیله وزن‌دهی هدفدار متغیرها 
2-3 الگوریتم ژنتیک پارتو مبتنی بر همسایگی
2-4 الگوریتم ژنتیک مرتب‌سازی غیرمغلوب 
3- مسئله کوله‌پشتی 
3-1 فرمول‌بندی یک مسئله بهینه‌سازی چندهدفه 
3-2 داده‌های آزمون 
3-3 کاربرد 
4- آزمایش‌ها 
4-1 روش‌شناسی
4-2 نتایج 
5- نتیجه‌گیری و چشم‌انداز آتی 
منابع

Abstract
1 Introduction
2 Multiobjective Evolutionary Algorithms
2.1 Vector Evaluated Genetic Algorithm
2.2 Aggregation by Variable Objective Weighting
2.3 Niched Pareto Genetic Algorithm
2.4 Nondominated Sorting Genetic Algorithm
3 The Knapsack Problem
3.1 Formulation as Multiobjective Optimization Problem
3.2 Test Data
3.3 Implementation
4 Experiments
4.1 Methodology
4.2 Results
5 Conclusions and Future Work
References