دانلود مقاله انحراف زمان پویای عمیق تکراری برای سری زمانی
1. مقدمه
سریهای زمانی، شکل فراگیری از دادهها هستند که تقریباً در هر رشته علمی و کاربردهای تجاری اتفاق میافتد. اخیراً کارهای بسیاری در زمینه سازگاری الگوریتمهای دادهکاوی با پایگاه دادههای سری زمانی انجام شده است. به عنوان مثال، داس و همکاران برای نشان دادن چگونگی آموختن قوانین ترکیبی سری زمانی تلاش کردند [7]. دبرگاس و هبریل در [8]، تکنیکی برای مقیاسگذاری الگوریتمهای خوشهبندی سری زمانی در مجموعه دادههای گسترده ارائه کردند. کغ و پازانی الگوریتم طبقهبندی سری زمانی جدید مقیاسپذیر را معرفی کردند [16]. تقریباً همه الگوریتمهایی که بر روی دادههای سری زمانی کار میکنند، باید شباهت بین آنها را محاسبه کنند. فاصله اقلیدسی یا برخی از پسوندها یا اصلاحات آن به طور معمول مورد استفاده قرار میگیرد. با این وجود، همانطور که در بخش 2-1 نشان خواهیم داد، فاصله اقلیدسی ممکن است در اندازهگیری فاصله بسیار ناپایدار باشد.
دلیل اینکه فاصله اقلیدسی ممکن است نتواند ارزیابی بصری صحیحی از شباهت بین دو بخش ایجاد کند، این است که به انحرافات کوچک در محور زمان بسیار حساس است. شکل 1-A را در نظر بگیرید، دو دنباله تقریباً شکل کلی یکسانی دارند اما اشکال در محور زمان تراز نیستند. تراز غیرخطی نشان داده شده در شکل 1-B باعث میشود که اندازه فاصله بصری بیشتری محاسبه شود.
روشی که این امکان را برای تغییر الاستیک محور X فراهم میکند به منظور تشخیص اشکال مشابه با فازهای مختلف میباشد. چنین روشی مدتهاست که در جامعه پردازش گفتار شناختهشده است [26 و 29]. روش انحراف زمان پویا (DTW) توسط برند و کلیفورد به جامعه دادهکاوی معرفی شد [4]. اگرچه آنها کاربرد این روش را نشان دادند اما اذعان کردند که پیچیدگی زمانی الگوریتم یک مشکل است و «... ممکن است عملکرد آن در بانکهای اطلاعاتی بسیار بزرگ محدودیت باشد». با وجود ایراد روش انحراف زمان پویا، هنوز هم در زمینههای مختلف مورد استفاده گسترده قرار میگیرد. در بیوانفورماتیک، آچ و چورچ با موفقیت از روش انحراف زمان پویا در بیان دادههای RNA استفاده کردند [1]. در مهندسی شیمی از آن برای هماهنگسازی و نظارت بر فرآیندهای دستهای در پلیمریزاسیون استفاده شد [14]. از روش انحراف زمان پویا با موفقیت برای تراز کردن دادههای بیومتریک، مانند راه رفتن، امضاها و حتی اثر انگشت استفاده شد [11، 14، 22، 19]. محققان متعددی از جمله وولینگز و همکاران [30] و کیانی و همکاران [5]، استفاده از روش انحراف زمان پویا را برای تطبیق الگوی ECG نشان دادند. سرانجام در رباتیک، اوتس و همکاران نشان دادند كه روش انحراف زمان پویا را میتوان براي خوشهبندي خروجيهاي حسي عامل مورد استفاده قرار داد [23].
6. نتایج و کار آتی
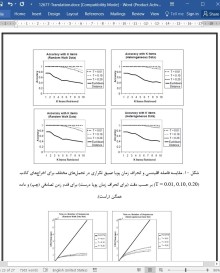
در این مقاله، اصلاح انحراف زمان پویا ارائه شد که ایده عمق تکراری را همراه با روش کاهش بعد برای تولید سرعت چشمگیر همراه با افزایش اندازه پایگاه داده به کار میگیرد. الگوریتم ما دارای ویژگیهای مطلوب شامل انحراف زمان پویا واقعی به عنوان حالت خاص (در حالت T = 0) و عدم نیاز به تنظیم دقیق پارامترهای سیستم است. علاوه بر این، روش ما کنترل کامل پایان- کاربر و واضحی را در کل مبادله کیفیت/ زمان تنها از طریق پارامتر بصری با تحمل آنها برای احتمال اخراج کاذب ارائه میدهد.
کار آتی شامل تحلیل جزئیات بیشتر روش ما و تعمیمات آن برای سایر مسائل جستجو مشابه است که ارزیابی فاصله بیشتر در آنها سنگین است اما میتوان در سطوح مختلف دقت تقریبسازی کرد.
1 Introduction
Time series are a ubiquitous form of data occurring in virtually every scientific discipline and business application. There has been much recent work on adapting data mining algorithms to time series databases. For example, Das et al. attempt to show how association rules can be learned from time series [7]. Debregeas and Hebrail [8] demonstrate a technique for scaling up time series clustering algorithms to massive datasets. Keogh and Pazzani introduced a new, scalable time series classification algorithm [16]. Almost all algorithms that operate on time series data need to compute the similarity between them. Euclidean distance, or some extension or modification thereof, is typically used. However as we will demonstrate in Section 2.1, Euclidean distance can be an extremely brittle distance measure.
The reason why Euclidean distance may fail to produce an intuitively correct measure of similarity between two sequences is that it is very sensitive to small distortions in the time axis. Consider Figure 1.A, the two sequences have approximately the same overall shape, but the shapes are not aligned in the time axis. The nonlinear alignment shown in Fig 1.B would allow a more intuitive distance measure to be calculated.
A method that allows this elastic shifting of the X-axis is desired in order to detect similar shapes with different phases. Such a technique has long been known in the speech processing community [29, 26]. The technique, Dynamic Time Warping (DTW), was introduced to the data mining community by Berndt and Clifford [4]. Although they demonstrate the utility of the approach, they acknowledge that the algorithm’s time complexity is a problem and that “…performance on very large databases may be a limitation”. Despite this shortcoming of DTW, it is still widely used in various fields. In bioinformatics, Aach and Church successfully applied DTW to RNA expression data [1]. In chemical engineering, it has been used for the synchronization and monitoring of batch processes in polymerization [14]. DTW has been successfully used to align biometric data, such as gait, signatures and even fingerprints [11, 14, 22, 19]. Several researchers including Vullings et al. [30] and Caiani et al. [5] have demonstrate the use of DTW for ECG pattern matching. Finally in robotics, Oates et al. demonstrated that DTW may be used for clustering an agent's sensory outputs [23].
6 Conclusions and Future Work
In this paper we introduced a modification of DTW that exploits the idea of iterative deepening along with a dimensionality reduction technique to produce a dramatic speedup which increases with database size. Our algorithm has the desirable properties of containing true DTW as a special case (when T = 0), and not requiring the careful adjustment of system parameters. In addition our approach gives the end-user complete and explicit control over the quality/time tradeoff through a single intuitive parameter, their tolerance for the probability of a false dismissal.
Future work includes a more detailed analysis of our approach and extensions to other similarity search problems that feature distance measures that are expensive, but can be approximated at different levels of precision.
1. مقدمه
2. پسزمینه
2-1. انحراف زمان پویا با فاصله اقلیدسی
2-1-1. دستهبندی
2-1-2. خوشهبندی
2-1-3. قواعد متناظر استخراج
2-2. الگوریتم انحراف زمان پویا
2-3. دلیل مقاومت انحراف زمان پویا به بهینهسازی
3. روش جدید: انحراف زمانی پویای عمیق تکراری
3-1. کاهش ابعاد
3-2. بینش الگوریتم عمیق تکراری
3-3. جزئیات الگوریتم عمیق تکراری
4. ارزیابی تجربی
4-1. نتایج و تحلیل
5. کارهای مربوطه
6. نتایج و کار آتی
منابع
1 Introduction
2 Background
2.1 Dynamic Time Warping vs. Euclidean Distance
2.1.1 Classification
2.1.2 Clustering
2.1.3 Mining Association Rules
2.2 The Dynamic Time Warping Algorithm
2.3 Why Dynamic Time Warping is Resistant to Optimization
3 A New Approach: Iterative Deepening Dynamic Time Warping
3.1 Dimensionality Reduction
3.2 Iterative Deepening Algorithm Intuition
3.3 Iterative Deepening Algorithm Details
4 Experimental Evaluation
4.1 Results and Analysis
5 Related Work
6 Conclusions and Future Work
References
- اصل مقاله انگلیسی با فرمت ورد (word) با قابلیت ویرایش
- ترجمه فارسی مقاله با فرمت ورد (word) با قابلیت ویرایش، بدون آرم سایت ای ترجمه
- ترجمه فارسی مقاله با فرمت pdf، بدون آرم سایت ای ترجمه