دانلود مقاله تحلیل کمانش و پایداری غیرخطی قوس های درجه بندی شده تابعی کامپوزیت در معرض فشار خارجی و بارگذاری دما

چکیده

     این مقاله به بررسی پایداری غیرخطی و رفتار کمانش قوس ها با مواد درجه بندی شده تابعی کامپوزیت (FGM) می پردازد که در عرض بارگذاری دما و فشار قرار دارند. با معرفی یک تابع جابجایی مجاز، انرژی پتانسیل کل به صراحت از نظریه  پوسته دیواره نازک پیروی می کند. معادلات تعادل غیرخطی با تغییر تابع انرژی پتانسیل محاسبه شده اند، و فشار کمانش بحرانی به صورت تحلیلی پیش بینی شده است. تایید با استفاده از شبیه سازی عددی انجام شده است که مسیرهای تعادل پیش و پس کمانش را دنبال می کند، این امر نشان می دهد که نتایج عددی با پیش بینی های تحلیلی مطابقت خوبی دارند. مشاهده شده است که افزایش دما منجر به افزایش جابجایی به سمت بالا شده، که برای فشار کمانش مفید بوده و مدول یانگ را کاهش می دهد، که برای فشار کمانش مفید نیست. بنابراین، فشار کمانش نسبت به افزایش دما غیرخطی است. در نهایت، مجموعه ای معادلات پارامتری در درجه اول روی اثرات توان کسری حجم وافزایش دما روی توزیع کرنش حلقه، تنش، نیرو و لنگر خمشی تمرکز دارد.

1. مقدمه

     مولفه های قوس، واحدهای اساسی در زیرساخت های عمرانی هستند. رفتار پایداری مولفه قوسی به دلیل نسبت ضخامت بالای آن مرسوم است که این امر نشان می دهد طول بسیار بیشتر از ابعاد مقطع عرضی است. بنابراین، بررسی پاسخ های کمانش ساختارهای قوسی اهمیت دارد. مطالعات موجود [7-1] نشان داد که عملکرد کمانش ناشی از تنش حلقه اضافی است، که حاصل از بارگذاری مکانیکی و/ یا اثرات دمایی است. هنگامی که قوس دچار کمانش می شود، تغییر شکل ممکن است مطابق با شکل 1 متقارن و یا نامتقارن باشد [10 – 8]. در تحقیق حاضر، بیشتر مکانیزم کمانش متقارن مورد نظر بوده و مکانیزم کمانش نامتقارن را نیز می توان با فرایندی مشابه مورد ارزیابی قرار داد. در ادامه نتایج شبیه سازی [12 و 11]، تغییرشکل نسبت به نقایص اولیه حساس است، که این امر نشان می دهد نتایج اولیه متقارن منجر به تغییرشکل متقارن و نتایج اولیه نامتقارن منجر به تغییرشکل نامتقارن می شوند. مواد تابعی درجه بندی شده (FGM) در دهه های اخیر به شکل گسترده ای مورد استفاده قرار گرفته اند. مفهوم FGM به دلیل اتلاف گرما از سطح خارجی هواپیما به دلیل عملکرد بالای مقاوت حرارتی آن پیشنهاد شد [13]. و پس از آن، FGM در زمینه های بسیار دیگری گسترش یافت، مانند نیروگاه های هسته ای، نیروگاه های حرارتی، و غیره. علاوه بر این، FGM به دلیل دستحکام و مقاومت بالای خود در برابر خوردگی همچنین در زمینه های بیولوژیکی برای استخوان های مصنوعی یا دندان ها، یا برای دستگاه هایی که در عمق دریا کار می کنند [14]. بسیاری از تحقیقات در رابطه با مکانیزم پایداری قوس های FGM بودند. یک قوس FGM مرسوم متشکل از دو ماده تشکیل دهنده با سفال غنی در سطح خارجی و و فلز غنی در سطح داخلی مطابق با شکل 2 است. اصغری و همکاران [15] مکانیزم کمانش قوس های FGM تحت اثر گرمایی را گزارش کردند. براساس طرح جابجایی مجازی، پیش بینی نظری افزایش دمای بحرانی حاصل گردید. نتیجه گیری شد که شکست مواد پیش از کمانش حرارحتی بوده است. باطنی و اسماعیلی [16]، مکانیزم فروپاشی قوس های FGM کم عمق را تحت بارهای متمرکز شعاعی مورد بررسی قرار دادند. هر دو قوس های گیردار و سوزنی مورد بحث قرار گرفته و بار کمانش به وسیله حل مجموعه ای معادلات تعادل غیرخطی بدست آمد. سوامیناتان و همکاران [17] مکانیزم کمانش صفحات FGM تحت بارگذاری ها، مرزها، نسبت های طول به عرض، و نسبت های طول به ضخامت مختلف را ارائه کردند. سیمسک [18] تیرهای FGM تیموشنکو دو بعدی را با روش ریتز مورد بررسی قرار داد. بار کمانش بحرانی به وسیله اشکال چندجمله ای محوری، جابجایی عرضی و چرخش سطح مقطع تیر پیش بینی شده است. اخیراً، مویتا و همکاران [19] اثر توزیه مواد بر رفتار کمانش سازه های FGM بر اساس نظریه تغییرشکل درجه بالاتر را گزارش کردند. 5 نوع مختلف از صفحات FGM و پانل ها مورد بررسی قرار گرفتند. الشوجیری و ملاامحموتوغلو [20] عملکرد کمانش تیرهای ساندویچی FGM تحت میدان تغییرات حرارتی را مورد بررسی قرار دادند. کمانش بحرانی با استفاده از روش کوادراتور دیفرانیسل تعمیم یافته بدست آمد.

5. نتیجه گیری ها
     مکانیزم پایداری قوس FGM زمانیکه در معرض فشاری خارجی و بارگذاری حرارتی قرار گرفته باشد مورد ارزیابی قرار گرفت. براساس بررسی های تحلیلی و عددی حاضر، چندین نتیجه گیری اصلی مورد تاکید قرار گرفته اند:
1.    فشار کمانش تحلیلی استخراج شده با استفاده از نتایج عددی هم برای قوس های گیردار- گیردار و هم برای قوس های سوزنی – سوزنی تایید شد. برای قوس همگن (n=0) نتایج تحلیلی و عددی حاضر با دیگر عبارات شکل بسته در دسترس سازگار است.
2.    تنش و کرنش قوس FGM (n>0)به صورتی متفاوت از قوس همگن توزیع شده که این امر ناشی از توزیع غیرمتقارن خواص مواد در مقطع عرضی است. 
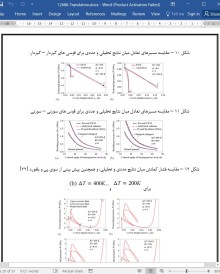
3.    افزایش دما منجر به جابجایی روبه به بالای شعاعی دمایی و کاهش مدول یانگ می شود، که به ترتیب برای فشار کمانش بحرانی قوس FGM مثبت و منفی هستند. 
4.    شماره لایه N=20 در جهت ضخامت به اندازه کافی دقیق است تا منجر به همگرایی فشار کمانش شود. بنابراین، B=20 برای تولیدکنندگان صنعتی سازه های FGM با دیواره نازک پیشنهاد شده است.
     تحقیق حاضر به طور عمده در رابطه با کمانش الاستیک قوس FGM است. تایید آزمایشگاهی بیشتر پیش از استفاده از آن در زمینه های مهندسی مورد نیاز است. علاوه بر این، خواص مواد غیرالاستیک در مدل حاضر نادیده گرفته شده اند. با این حال، ممکن است در سیستم های عملی موجود باشند و تاثیر قابل توجهی روی فشار کمانش داشته باشند. 

Abstract

     This paper investigates the nonlinear stability and buckling behavior of the composite functionally graded material (FGM) arches subjected to pressure and temperature loadings. By introducing an admissible displacement function, the total potential energy is expressed explicitly following the thin-walled shell theory. The nonlinear equilibrium equations are calculated by the variation of the potential energy function, and the critical buckling pressure is predicted analytically. The verification is taken by the numerical simulation that traces the pre- and post-buckling equilibrium paths, indicating that the numerical results are in good accordance with the analytical predictions. It is found the temperature rise increases the thermal upward displacement, which is beneficial to the buckling pressure, and reduces Young’s modulus, which is unbeneficial to the buckling pressure. Therefore, the buckling pressure is nonlinear to the temperature rise. Finally, a series of parametric evaluations are mainly focused on the effects of volume fraction exponent and temperature rise on the distributions of hoop strain, stress, force and bending moment.

1. Introduction

     Arch elements are the basic units in civil infrastructures. The instability behavior of the arch element is common due to its high slenderness ratio, indicating the length is much higher than the dimensions of the cross-section. Therefore, it is significant to study the buckling responses of the arch structures. Existing studies [1–7] found that the buckling performance was induced by excessive hoop stress, which results from the mechanical loadings and/or thermal effects. When the arch buckles, the deformation may be symmetrical or asymmetrical as shown in Fig. 1 [8–10]. In the present investigation, the symmetrical buckling mechanism is mainly concerned, and the asymmetrical buckling mechanism can also be evaluated with a similar derivation procedure. Following the simulation results [11,12], the deformation is sensitive to the initial imperfection, indicating symmetrical initial imperfection results in symmetrical deformed shape and asymmetrical initial imperfection results in asymmetrical deformed shape, respectively.

     Functionally graded materials (FGM) have been widely used in recent several decades. The concept of the FGM was proposed to dissipate the heat of the outer surface of the aircraft due to its high performance of thermal resistance [13]. And then, the FGM was extended in many other fields, such as nuclear power plants, thermal power plants and so on. In addition, the FGM was also used in the biological field for artificial bones or teeth, or in deep-sea apparatus for its high strength and corrosion resistance [14]. Many studies were concerned with the stability mechanism of the FGM arches. A typical FGM arch consists of two constituents with ceramic rich in outside surface and metal rich in inside surface as depicted in Fig. 2. Asgari et al. [15] reported the buckling mechanism of the FGM arches under thermal effect. Based on the scheme of virtual displacement, the theoretical prediction of the critical temperature rise was obtained. It was concluded that material failure was prior to the thermal buckling. Bateni and Eslami [16] studied the collapse mechanism of the shallow FGM arches under a radially-directed concentrated load. Both pinned-pinned and clampedclamped FGM arches were discussed and the buckling load was predicted by solving a set of nonlinear equilibrium equation. Swaminathan et al. [17] presented the buckling mechanism of the FGM plates under different loadings types, boundaries, length-to-width ratios, and lengthto-thickness ratios. Simsek [18] examined the two-dimensional Timoshenko FGM beams with the Ritz method. The critical buckling load is predicted by taking polynomial forms of the axial, transverse displacement and rotation of the beam cross-sections. Recently, Moita et al. [19] reported the effect of material distribution on the buckling behavior of the FGM structures based on the theory of higher-order deformation. Five different types of FGM plates and panels were examined. Al-shujairi and Mollamahmutoğlu [20] examined the buckling performance of FGM sandwich beams under the thermal variational field. The critical buckling load was obtained by using the generalized differential quadrature method.

5. Conclusions

    The stability mechanism of the FGM arch is evaluated when it is subjected to external pressure and thermal loading. Based on the present analytical and numerical investigation, several main conclusions are emphasized:

(1) The derived analytical buckling pressure is verified successfully by the numerical results for both clamped-clamped and pinned-pinned arches, respectively. For a homogenous arch (n = 0), the present analytical and numerical results are consistent with available other closed-form expressions.

(2) The strain and stress of the FGM arch (n > 0) are distributed differently from the homogeneous arch due to the non-symmetrical distribution of the material properties in the cross-section.

(3) The temperature rise generates a thermal radially-outward displacement and a reduction on Young’s modulus, which are positive and negative to the critical buckling pressure of the FGM arch, respectively.

(4) The layer number N = 20 in the thickness direction is accurate enough to converge the buckling pressure. Therefore, N = 20 is recommended to industrial manufacturing of the thin-walled FGM structures.

     The present investigation is mainly concerned with the elastic buckling of the FGM arch. Further experimental verification is necessary before it is applied to engineering applications. In addition, the inelastic material properties are ignored in the present model. However, they may exist in practical systems and have significant effects on the buckling pressure.

(جهت بزرگ نمایی روی عکس کلیک نمایید)

چکیده
1. مقدمه
2. فرضیات و شکل گیری معادلات تعادل
3. تعیین فشار کمانش بحرانی
3.1 قوس های انتهایی گیردار - گیردار
3.2 قوس های انتهایی سوزنی – سوزنی
4. تحلیل عددی
4.1 تعریف مدل عددی
4.2 مقایسه ها و بحث ها
4.3 ارزیابی های پارارمتری
5. نتیجه گیری ها
منابع

ABSTRACT
1. Introduction
2. Assumptions and formation of equilibrium equations
3. Determination of critical buckling pressure
3.1. Clamped-clamped ends arch
3.2. Pinned-pinned ends arch
4. Numerical analysis
4.1. Definition of the numerical model
4.2. Comparisons and discussions
4.3. Parametric evaluations
5. Conclusions
References