دانلود رایگان مقاله مکانیسم هم رسوبی سیلیکون کاربید با کبالت الکترولیت

چکیده

       مکانیسم هم رسوبي برای کاربید سیلیکون با کبالت الکترولیت مورد مطالعه قرار گرفت. یک مدل نظری از هم رسوبي در اینجا توسعه داده شده که بینشی کامل تر به مکانیزم هم رسوبي الکترولیتی را از مدل Guglielmi فراهم می کند. این مدل بیان عمومی تر در رابطه با درصد وزن ذرات تعبیه شده برای چگالی جریان در غلظت ذرات تعلیق مختلف برای سیستم هم رسوبي CO-SiC را ارائه می دهد که نمی تواند توسط مدل Guglielmi توصیف شود.

        علاقه به پوشش های کامپوزیت رسوب شده الکترود به سرعت با توجه به برنامه های کاربردی مهندسی جدید مورد انتظار آنها افزایش یافته است. چنین پوشش هایی توسط هم رسوبي ذرات ریز خنثی در ماتریس فلزی از الکترولیت یا حمام الکترولس تولید می شوند. به عنوان مثال، یک پوشش کبالت در رابطه با ذرات کربید سیلیکون توسعه داده شد و بسیار موفق ثابت شده است.

         اگر چه این تکنیک به طور قابل ملاحظه ای از نقطه نظر عملی توسعه داده شده است، جزئیات نظری در مکانیسم هم رسوبي به خوبی درک نمی شود. سه مکانیسم، یعنی، گنجاندن مکانیکی، الکتروفورز، و جذب ذرات خنثی بر روی کاتد، برای توضیح هم رسوبي مشاهده شده پیشنهاد شده است. اهمیت نسبی این سه فرایند را نمی توان از کار تجربی به صورت برخی از نتایج ضد و نقیض استنباط نمود. Guglielmi  یک مدل ریاضی برای رسوب الکترود ذرات خنثی پیشنهاد کرده است که بر اساس جذب دو مرحله پی در پی است. در مرحله اول جذب شل وجود دارد که اساسا دارای شخصیت فیزیکی است که نتایج آن درجه بالایی از پوشش کاتد توسط ذراتی است که در تعادل با ذرات در محلول تعلیق قرار دارند. این ذرات هنوز هم در محاصره یون های جذب  شده و مولکولهای حلال هستند. در مرحله دوم این نمایش تجزیه می شود به طوری که جذب الکتروشیمیایی قوی ذرات در کاتد صورت می گیرد، یعنی، جذب قوی. ذرات خنثی جریان به طور دائم متصل به کاتد هستند و به تبع آن در رسوب گنجانده می شوند. فرمول بنابراین استنباط این است که در آن CP غلظت ذرات معلق، α کسر حجمی ذرات در رسوب، F، W، و d ثابت فارادی، وزن اتمی و چگالی رسوب شده الکترود فلز، به دست آمد. پارامترهای i0 و A مربوط به رسوب فلز و در معادله Tafel ثابت هستند. به طور مشابه، پارامتر V0 و B مربوط به رسوب ذرات خنثی است. K از ایزوترم جذب لانگمور مشتق شده است و اساسا به شدت تعامل بین ذرات و کاتد بستگی دارد. اعتبار این مدل برای سیستم های هم رسوبي مختلف مانند SiC و ساختار TiO2 با نیکل از حمام sulfamate، -A1203 با مس از حمام اسیدی سولفات مس، A1203 با نیکل از حمام واتس، و TiQ2 با مس از حمام سولفات مس اسیدی تایید شده است. با این حال، برخی از سیستم های هم رسوبي از کلیت این مدل سوال می کنند، مانند -AL - O3α با مس از حمام سولفات مس اسید و A1203 با طلا از حمام سیانید. مدل Guglielmi می تواند درصد وزن ذرات در رسوب ها و جریان رابطه چگالی نشان داده شده در شکل 1 را توصیف نماید. مدل کلی تری برای سیستم هم رسوبي باید توسعه داده شود.

         Foster و Kariapper یک عبارت ریاضی را پیشنهاد نموده اند که می تواند اثر علم نیرو وجنبش را توصیف نماید. Ceils و همکاران یک مدل ریاضی از یک رویکرد آماری از اختلاط ذرات پیشنهاد نموده اند. به علت روابط پیچیده بین برخی از این عوامل (چگالی جریان انتقال، چگالی جریان محدود کننده، مقدار یون جذب شده بر روی ذرات، انتشار ضخامت لایه، پارامتر تعامل بین آزاد و جذب یون ها با توجه به اثر چگالی جریان، و غیره)، مقدار کار محدودی برای اثبات اعتبار این دو مدل انجام شده است.

        مدل کلی تری در اینجا برای توصیف مکانیسم روند هم رسوبي الکترولیتی پیشنهاد می شود و توسط نتایج تجربی از سیستم کبالت کاربید سیلیکون الکترولیتی تایید شده است.

تجربی

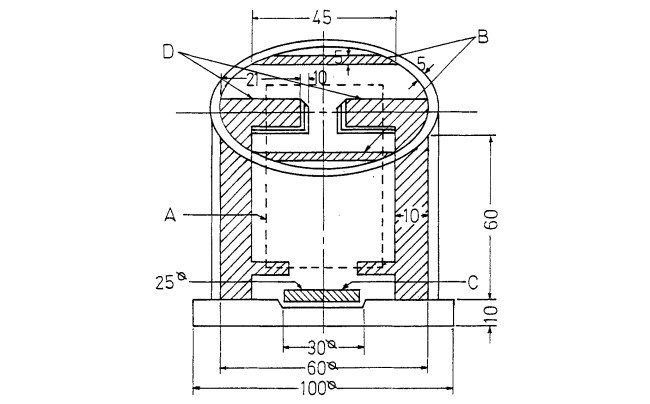
        قدرت درجه ساینده کاربید سیلیکون (مواد شیمیایی Yakuri (α-SiC) برای 3μm برای بررسی مورد استفاده قرار گرفت. پودر کاملا در استون حلال پاک شد. و با اسید نیتریک رقیق گرم برای حذف هر گونه ناخالصی آلی پرداخت شد، به طور کامل در آب مقطر شسته و خشک شد. تمام مواد شیمیایی در درجه معرف بودند و بدون تصفیه بیشتر استفاده شدند. حمام سولفات کبالت با حل شدن 100 گرم / DM 3 CoSQ 9 7H20، 15 گرم / DIN 3 CoC12 9 6H20، 10 گرم / DM 3 KC1، و 25 گرم / DM و 3 H3BO3 در آب مقطر آماده سازی شد. آزمایش آبکاری در یک راکتور اکریلیک با دو تیغه (شکل 2) انجام شد. کاتدهای برنج عمودی در مرکز راکتور طراحی شده قرار داده شدند به طوری که یکنواختی خوبی از رسوبات می تواند به دست آید. یکنواختی چگالی جریان در راکتور طراحی شده از توزیع ذرات رسوب شده توسط میکروسکوپ نوری کنترل شد. نتایج نشان می دهد که یکنواختی خوب در راکتور طراحی شده به دست آمده است. غلظت پودر سیلیکون کاربید استفاده شده در تعلیق در الکترولیت از 2-10 g/dm3 تغییر می نمود. حمام در 30±1 درجه راه اندازی شد، چگالی جریان به کار گرفته شده در محدوده برابر 0.1 تا 6 DM / 2 بود، pH در 4 کنترل می شد و تعداد کلی کولن 310 C در هر دسته بود. ورقه های کبالت الکترولیت به عنوان آند به کار گرفته شدند در حالی که برنج به عنوان کاتد بودند. در این نوع باتری، الکترودها در روش معمول متصل شدند.

منبع تغذیه به صورت منبع جریان مستقیم به کار گرفته شد. حمام با میله پوشش تفلون مغناطیسی نوار به کار انداخته شد. میزان ترکیب در 400 دور در دقیقه کنترل شد. وزن کل رسوب ها توسط تعادل بسیار ریز مشخص شد. درصد وزن کاربید سیلیکون در رسوب ها توسط طیف سنجی فلورسنت اشعه ایکس مورد تجزیه و تحلیل قرار گرفت. قبل از این اندازه گیری، استانداردهای آماده شده و رسوبها زمین شدند و با 1μm تعلیق الماس در rpm 150 و N100 و به مدت 20 ثانیه صیقل شدند (Struers، Abramin).

مدل نظری 

        شرح مدل - همانطور که در شکل 3 نشان داده شده است، لایه جذب شده از گونه های یونی اطراف ذرات خنثی ایجاد شد در حالی که ذرات به محلول آبکاری اضافه شدند. روش آن از محلول حجمی به رسوب ذرات خنثی از طریق سه مرحله ادامه می یابد (I) ذرات عمدتا توسط همرفت اجباری انتقال پیدا کردند (ب) ذرات با ابر جذب شده یونی خود آزادانه در سطح کاتدی جذب شدند و (III) ذرات به طور برگشت ناپذیر در ماتریس فلزی توسط کاهش برخی از یونهای جذب شده گنجانیده شدند. یونهای CO 2 در محلول حجمی از طریق لایه انتشار پخش می شوند و بر روی سطح کاتد برای برآورده کردن خواسته های روند کاهش رسوب می شوند. جریان جزئی به منظور کاهش یون های + H مصرف می شود که از طریق لایه انتشار از محلول حجمی پخش می شوند. یون جذبی پیشنهاد شده + H و CO 2+ هستند. در حالت پایدار، یک لایه انتشار و مشخصات غلظت بر روی سطح ذرات گسترش می یابد همانطور که در شکل 4 نشان داده شده است. هنگامی که چگالی جریان اعمال شده کم باشد، یون های جذبی +H در ذرات کاهش می یابند. شیب غلظت یون های H+ روی ذره همانطور که در شکل 4b نشان داده شده است، توسعه می یابد. افزایش چگالی جریان، باعث کاهش غلظت یون ذره H + می شود. غلظت H + یون بر روی ذره در مورد محدودکننده به (شکل 4C) صفر نزدیک می شود. اگر چگالی جریان بیشتر افزایش یابد، هر دو غلظت یون های جذبی H + و Co 2 + بر روی ذرات کاهش می یابد. شیب غلظت یون های H + و Co 2 + توسعه می یابد (شکل 4D). غلظت یون های H + و Co 2 + بر روی سطح ذرات به صفر می رسد (شکل 4E).

ABSTRACT

        The mechanism of codeposition of silicon carbide with electrolytic cobalt was studied. A theoretical model of codeposition is developed here which provides a more complete insight to the mechanism of electrolytic codeposition than Guglielmi's model. The model gives a more general expression relating weight percent of embedded particles to current density for different suspension particle concentration for the Co-SiC codeposition system which cannot be described by Guglielmi's model.

         Interest in electrodeposited composite coatings has increased rapidly 16 due to their expected new engineering applications. ~ Such coatings are produced by codeposition of fine inert particles in a metal matrix from electrolytic or electroless baths. For example, a cobalt coating in conjunction with silicon carbide particles was developed and has been proven highly successful.

         Although the technique has been developed considerably from the practical point of view, the theoretical details on the codeposition mechanism are not well understood. Three mechanisms, namely, mechanical inclusion, electrophoresis, and adsorption of inert particles onto the cathode, have been proposed to explain the observed codeposition. The relative importance of these three processes cannot be deduced from published experimental work as some results are contradictory. Guglielmi 7 has proposed a mathematical model for the electrodeposition of inert particles which is based on two successive adsorption steps. In the first step a loose adsorption which has an essentially physical character results in a high degree of coverage of cathode by particles which are in equilibrium with the particles in suspension solution. The particles are still surrounded by adsorbed ions and solvent molecules. In the second step this screen is broken through so that a strong electrochemical adsorption of the particles on the cathode takes place, namely, strong adsorption. The inert particles are now permanently bound to the cathode and consequently are embedded in the deposit. The formula so deduced is Where Cp is the concentration of suspended particles, a is the volume fraction of particles in the deposit, F, W,, and d are the Faraday constant, atomic weight, and density of the electrodeposited metal, respectively. The parameters i0 and A are related to the metal deposition and are the constants in the Tafel equation. Similarly, the parameters v0 and B are related to the inert particle deposition. K is derived from the Langmuir adsorption isotherm and depends essentially on the intensity of the interaction between particles and cathode. The validity of this model has been verified for different codeposition systems such as SiC and TiO2 with nickel from sulfamate baths, 7 a-A1203 with copper from acid copper sulfate baths, 8 A1203 with nickel from Watts bath, 9 and TiQ with copper from acidic copper sulfate baths. ~~ However, some codeposition systems question the generality of the model, such as ~-Al~O3 with copper from acid copper sulfate baths ~ and A12Q with gold from cyanide baths. ~ Guglielmi's model cannot describe the weight percent of the particles in the deposit and the current density relationship shown in Fig. 1. A more general model for the codeposition system must be developed.

       Foster and Kariapper ~ have proposed a mathematical expression that could describe the effect of hydrodynamics. Cells et al. ~2 have proposed a mathematical model from a statistical approach of the incorporation of particles. Because of the complex interrelationship between some of these factors (transition current density, limiting current density, amount of ions adsorbed on particles, diffusion layer thickness, interaction parameter between free and adsorbed ions due to current density effect, etc.), a limited amount of work was done to prove the validity of these two models.

        A more general model is proposed here to describe the mechanism of the electrolytic codeposition process and it is verified by experimental results of a silicon carbide-electrolytic cobalt system.

Experimental

        Abrasive grade silicon carbide powers (Yakuri chemicals, (~-SiC) of 3 ~m were used for the investigation. The powders were thoroughly cleaned in an acetone solvent, and treated with hot dilute nitric acid to remove any organic impurities, washed thoroughly in distilled water, and dried. All chemicals were of reagent grade and used without further purification. A cobalt sulfate bath was prepared by dissolving 100 g/dm 3 CoSQ 9 7H20, 15 g/din 3 CoC12 9 6H20, 10 g/dm 3 KC1, and 25 g/dm 3 H3BO3 in distilled water. The plating experiments were conducted in an acrylic reactor with two baffles (Fig. 2). The vertical brass cathodes were placed on the center of the designed reactor so that a good uniformity of the deposits could be obtained. The unifortuity of current density in the designed reactor was checked from the distribution of deposited particles by the optical microscopy. The results indicate that a good uniformity is obtained in the designed reactor. The concentration of silicon carbide powder used in suspension in the electrolyte was varied from 2-10 g/dm 3. The bath was operated at 30 _+ I~ the current density employed was in the range 0.1 to 6 A/dm 2, pH was controlled at 4 and the total number of coulombs supplied was 310 C per batch. Sheets of electrolytic cobalt served as anodes while brass served as cathodes. The electrodes were pretreated in the usual way.

        A power supply served as the direct current source. The bath was agitated with a magnetically driven Tefloncoated stirring bar. The mixing rate was controlled at 400 rpm. The total weight of the deposits was determined by microbalance. The weight percent of silicon carbide in the deposits was analyzed by x-ray fluorescent spectrometry. Before this measurement, the prepared standards and deposits were ground and polished with i ~m diamond suspension at 150 rpm and 100 N for 20 s (Struers, Abramin).

Theoretical Model

        Model description.--As shown in Fig. 3, an adsorbed layer of ionic species is created around the inert particles while the particles are added to the plating solution. 12. On its way from the bulk solution to deposit the inert particle must proceed through three stages; (i) the particles are transferred primarily by forced convection; (ii) the particles with their adsorbed ionic cloud are adsorbed loosely at the cathode surfaceT; and (iii) the particles are incorporated irreversibly into the metal matrix by the reduction of some of the adsorbed ions. The Co +2 ions in the bulk solution diffuse through the diffusion layer and are deposited on the cathode surface to meet the demands of the reduction process. The partial current is consumed to reduce H § ions which diffuse through the diffusion layer from the bulk solution. The adsorbed ions proposed are H + and Co 2§ ions. At steady state, a diffusion layer and concentration profile on the particle surface develop as shown in Fig. 4. When the applied current density is low, the adsorbed H § ions on the particle are reduced first. A concentration gradient of H § ions on the particle develops as shown in Fig. 4b. Increasing the current density, decreases the concentration of H + ion on the particle. The concentration of H + ions on the particle approaches zero at limiting case (Fig. 4c). If the current density increases further, both the concentrations of adsorbed H + and Co 2+ ions on the particle are reduced. The concentration gradients of H + and Co 2+ ions develop (Fig. 4d). The concentrations os both H + and Co 2+ ions on the particle surface approach zero (Fig. 4e).

چکیده

تجربی

مدل نظری 

نتایج و بررسی ها

نتیجه

منابع

چکیده

ABSTRACT

Experimental

Theoretical Model

Results and Discussion

Conclusion

REFERENCES

ABSTRACT