دانلود رایگان مقاله مدلسازی و حداکثرسازی عملکرد در یک سیستم وسیله نقلیه هدایت شده خودکار

چکیده

        هدف از این مطالعه، مدل سازی و به حداکثر رساندن یک سیستم وسیله نقلیه هدایت شده خودکار ادغام شده (AGVS) است که در یک سیستم تولید انعطاف پذیر چند محصول، چند مرحله ای و چند خطی نوع کششی (FMS) جاسازی می شود. این مطالعه, تاثیر انعطاف پذیری مسیر-هدایت بر عملکرد سیستم را از طریق توسعه سه پیکربندی مسیر-هدایت مختلف بررسی می کند که اعم از مورد اختصاص داده شده به روابط انعطاف پذیر بین وسایل نقلیه هدایت شده خودکار (AGV) و منابع ایستگاه ماشین / مونتاژ می باشد. این سیستم با استفاده از روش شبکه رنگی پتری (CPN) مدلسازی می شود و نتایج شبیه سازی منجر به شناسایی ازدیاد منبع می شود که از طریق توسعه پیکربندی های مسیر-هدایت انعطاف پذیر برای دستیابی به هزینه پایین تر سیستم قابل اصلاح می باشد. این مطالعه با جستجوی شرایط کلی نزدیک به بهینه برای هر پیکربندی مسیر-هدایت با استفاده از روش سطح پاسخ گسترش می یابد که بهبودهایی را در کارایی سیستم و زمان چرخه همراه با کاهش تعداد AGVs حاصل می نماید.

1. مقدمه

        در محیط های تولید مدرن، سیستم های وسایل نقلیه هدایت شده خودکار به بخشی جدایی ناپذیر از سیستم های تولید کلی تبدیل شده اند. یک AGVS حاوی یک یا چند وسیله نقلیه هدایت شده خودکار می باشد که وسایل نقلیه بدون راننده ای هستند که برای حرکت افقی مواد استفاده می شوند. AGVها معمولاً در تاسیساتی مانند کارخانه های تولید، مراکز توزیع، انبارها و انتقال به کشتی یا وسیله حمل و نقل دیگر استفاده می شوند. AGVهای مورد مطالعه در این مقاله, یک سیستم دینامیکی (پویا) رویداد گسسته (DEDS) است، یعنی یک سیستم پویا با تغییرات وضعیتی ناشی از وقوع رویدادهای منفرد. این DEDS دارای ماهیت رویداد-محور، آسنکرون و غیرقطعی است. همچنین AGVS در نظر گرفته شده با FMS ادغام می شود و با سیستم تولید / مونتاژ انعطاف پذیر تعامل دارد. شبکه پتری، تکنیک های قدرتمند برای مدل سازی چنین سیستم هایی هستند, زیرا می توانند مفاهیم و محدودیت های مدلسازی پیچیده سیستم را مدیریت کنند. علاوه بر این، شبکه رنگی پتری (CPN), مدل های فشرده سیستم های بزرگ را با سطح بالایی از بهبود ارائه می دهند (Desrochers & Al-Jaar، 1995). از این رو، این مطالعه از روش CPN برای مدلسازی سیستم استفاده می کند و داده های تولید شده توسط مدل CPN برای توسعه مدل های سطح پاسخ به منظور بررسی شرایط نزدیک به بهینه در سیستم استفاده می شود.

2. کار مرتبط و منشا

        بیشتر مطالعات تحقیقاتی زمانبندی ماشین فرض می کنند که تعداد نامحدودی از حمل و نقل کننده ها برای ارائه کارها وجود دارند و یا اینکه شغل ها بدون زمان حمل و نقل دخیل, به طور لحظه ای از یک مکان به مکان دیگر تحویل می شوند (Lee & Chen، 2001). اکثریت کار تحقیقاتی موجود در نوشته های مدلسازی FMS، تنها مدلسازی پردازش مواد از طریق مراکز کاری را در نظر می گیرد و دسترسی بی وقفه به تجهیزات حمل و نقل ماده را در نظر می گیرد. این می تواند برای سیستم تولید نقاله ای معتبر باشد، اما برای سیستم های مبتنی بر AGV (Tamer، Abdelmaguid, Ashraf, Kamal, & Hassan, 2004) معقول نیست. محققان متعددی تاکید کرده اند که برنامه ریزی کارآمد سیستم حمل و نقل مواد برای بازده کلی FMS بسیار حیاتی است (Ulusoy & Bilge، 1993). ادغام سیستم حمل و نقل مواد (MHS) با فعالیت های تولیدی می تواند منجر به تولید سیستم هایی با مشخصه انعطاف پذیری، بهره وری بالا و هزینه کم در واحد تولیدشده منجر شود (Jawahar, Aravindan, Ponnambalam, & Suresh ، 1998). مشکلات مربوط به هماهنگی بهینه زمانبندی ماشین و حمل و نقل کار قطعاً عملی تر از مشکلات زمانبندی شده هستند که این عوامل را در نظر نمی گیرند. همچنین برای بهینه سازی کلی بین فعالیت های پردازش مواد و حمل و نقل مواد، برنامه ریزی تولید باید این دو عمل را به طور همزمان در نظر بگیرد (Seo & Egbelu، 1999). با این وجود، ادغام MHS با FMS، ناگزیر پیچیدگی یک مشکل را افزایش می دهد زیرا شامل تصمیمات پیوسته با فعالیت های پردازش مواد و انتقال مواد می شود (Lee & Chen، 2001). اولین مقاله زمانبندی که به صراحت عامل حمل و نقل را در نظر می گیرد، احتمالا توسط Maggu  و Das  (1980) انجام شده است. آنها یک مساله مدت زمان کار فروشگاه جریان دو-ماشین با فضاهای بافر نامحدود در هر دو ماشین را در نظر گرفتند که در آن تعداد کافی از حمل و نقل کننده ها وجود دارند، به طوری که هر زمانی که در اولین ماشین, یک کار تکمیل می شد، می توانست با زمان حمل و نقل وابسته به-کار, فوراً به ماشین دوم منتقل شود. Maggu, Das,  و  Kumar (1981), همین مسئله را با محدودیت اضافی در نظر گرفتند که برخی از کارها باید به طور ترتیبی زانبندی شوند. Kise (1991) مسئله مشابهی را بررسی کردند اما تنها با یک حمل و نقل کننده با ظرفیت یک و نشان دادند که این مسئله, NP-سخت است، حتی با زمان های حمل و نقل مستقل از کار. Stern و Vitner (1990), یک یک مساله مدت زمان کار فروشگاه جریان دو-ماشین را که در آن یک حمل و نقل کننده با ظرفیت یک وجود دارد، در نظر گرفتند. آنها تصور می کردند که زمان های حمل و نقل, وابسته به کار هستند و اینکه هیچ فضای بافر میانی در هر یک از دو ماشین وجود ندارد. آنها این مسئله را به عنوان یک مسئله فروشنده در حال حرکت نامتقارن مطرح کردند و یک ابتکار چندجمله ای-زمانی را ارائه دادند. Panwalker (1991) همان مسئله را در نظر گرفت، به جز اینکه فضای بافر در ماشین دوم, نامحدود باشد. او یک الگوریتم بهینه چندجمله ای-زمانی را ارائه کرد. فرایندهای طراحی و کنترل یک AGVS شامل مسائل بسیاری می شود (Vis، 2006) از جمله:

• طرح مسیر-هدایت،

• مدیریت ترافیك: پیش بینی و اجتناب از تصادفات و تنگناها,

• شماره و محل نقاط جمع آوری و تحویل،

• الزامات وسیله نقلیه

• اعزام، مسیریابی و زمانبندی وسیله نقلیه،

• موقعیت یابی وسیله نقلیه های بیکار (آماده به کار)

• مدیریت باتری و

• مدیریت وقوع خرابی

        در میان این عوامل، طرح پیکربندی مسیر-هدایت یا مسیر-جریان را می توان به عنوان یک مسئله در سطح راهبردی در نظر گرفت (Le-Anh & De Koster، 2006). طرح مسیر-هدایت, عملکرد یک سیستم را تحت تأثیر قرار می دهد، زیرا بر زمان سفر برای حمل بار از مبدا آن به مقصد آن، تعداد وسایل نقلیه مورد نیاز و میزان ازدحام تاثیر می گذارد (Seo & Egbelu، 1999). رایج ترين معيار عملكرد در طراحي مسیر-هدایت، حداقل سازی مجموع فاصله سفر وسیله نقلیه با توجه به طرح و جریان های معین است (Gaskins & Tanchoco، 1987؛ Kaspi & Tanchoco، 1990). جهت سفر AVGs در امتداد مسیر-هدایت ممکن است یکطرفه، دو طرفه یا ترکیبی از مسیرهای یکطرفه و دو طرفه باشد. سایر توسعه ها در طراحی مسیر جریان, عبارتند از تک حلقه ها، پیکربندهای پشت سر هم و پیکربندی های جریان تقسیم بندی شده. پیکربندی مسیرهای جریان ترکیبی یکطرفه و دو طرفه در (Rajotia، Shankar، & Batra، 1998) با هدف کاهش فاصله سفر مورد بررسی قرار گرفت. این نشان داد که می توان مزایایی را از نظر نرخ کارایی و اندازه ناوگان وسیله نقلیه به دست آورد, در حالیکه نرخ ازدحام وسیله نقلیه افزایش یافت و کنترل ترافیک اهمیت بیشتری پیدا نمود. Gaskins و Tanchoco  (1987) یکی از نخستین کسانی بودند که مسئله طرح مسیر-هدایت AGV با قوسهای یک طرفه را مورد بحث قرار دادند. این مشکل به صورت یک شبکه ارائه شد و به عنوان یک مدل برنامه نویسی خطی عدد صحیح 1-0 فرموله شد. هدف, مینیمم سازی فاصله مجموع حمل و نقل AGVها بود. Kaspi و Tanchoco  (1990) یک مدل با محدودیت های اضافی را توصیف کردند و یک روش کارآمد محاسباتی را ارائه دادند, یعنی رویکرد شاخه و حد که توسط Kim و Tanchoco  (1993) با در نظر گرفتن هزینه های ثابت برای ساخت و ساز، کنترل و فضای سیستم گسترش یافت. Ko و Egbelu  (2003) اظهار داشتند که در محیط تولید پویای امروز، تغییر ترکیبات محصول و مسیرهای ماشین، واقع بینانه است. آنها یک ابتکار برای طراحی شبکه های AGV را پیشنهاد و آزمایش کردند که می توانست به تغییرات حجم تولید و الگوهای جریان پاسخ دهد. Asef-Vaziri, Laporte, and Sriskandarajah (2000), مسئله طراحی کوتاهترین حلقه را به عنوان یک مدل برنامه نویسی خطی عددی فرموله کردند. Bilge وUlusoy  (1995) مساله زمانبندی تولید و حمل و نقل مواد ادغام شده را با هدف کاهش زمان تولید در یک FMS در نظر گرفتند. Lee و DiCesare  (1994)، زمانبندی تولید و حمل و نقل مواد ادغام شده در زمینه یک فروشگاه-کار را مورد مطالعه قرار دادند. یک شبکه پتری ارائه شد و یک روش اکتشافی پیشنهاد شد. هدف این بود که فاصله زمانی کل به حداقل برسد. آنها یک مغازه با سه ماشین و یک ربات برای فعالیت های تبدیل و پنج AGV برای فعالیت های انتقال مواد را در نظر گرفتند. دو مورد ارائه شد. در مورد اول، AGV به یک کار اختصاص داده شد، که تا پایان پردازش, با آن همراه بود. در مورد دوم، AGV به یک ماشین اختصاص داده شد که پس از پردازش توسط ماشین, کارها را منتقل نماید. دو AGV به ایستگاه بارگیری / تخلیه بار اختصاص داده شدند. (Sabuncuoglu & Hommertzheim، 1992a، 1992b), زمانبندی تولید و حمل و نقل مواد یکپارچه (ادغام شده) را برای یک FMS با یک محیط تولید فروشگاه-کار مورد مطالعه قرار دادند. برای ارزیابی عملکرد قواعد زمانبندی، شبیه سازی استفاده شد. هدف در نظر گرفته شده, به حداقل رساندن زمان جریان متوسط بود. روش شبیه سازی برای مدلسازي پیکربندی های سنتی، پشت سر هم و پشت سر هم / حلقه در (Farling، Mosier، & Mahmood، 2001) استفاده شد و مزایا و محدودیت های هر پیکربندی مورد بحث قرار گرفت. Aized، Takahashi و Hagiwara (2007a), مدل رنگی شبکه پتری و تحلیل FMS چند محصوله با تجزیه منبع و بازرسی خودکار را ارائه دادند. این مطالعه, مسائل مربوط به حمل و نقل مواد را در نظر نگرفت و دسترسی بی وقفه به وسایل نقلیه هدایت شده خودکار اختصاصی را فرض نمود. Aized، Aized, Takahashi و Hagiwara  (2007b) یک سیستم یکپارچه وسیله نقلیه هدایت شده خودکار را با استفاده از شبکه رنگی پتری مدلسازی و تحلیل کردند، اما در این مقاله, هیچ طرحی برای حداکثرسازی عملکرد با در نظر گرفتن عوامل متعدد ورودی به طور همزمان بحث نشده است. 

        در این مطالعه یک AGVS با یک FMS ادغام شده است و تعاملات بین FMS و AGVS مدل سازی می شوند و بهینه سازی سیستم با استفاده از روش سطح پاسخ انجام می شود. سهم این مطالعه این است که تاثیر انعطاف پذیری بر عملکرد یک AGVS یکپارچه را از طریق توسعه پیکربندیهای مختلف مسیر-هدایت تحلیل می کند. این پیکربندی ها به گونه ای طراحی شده اند که انعطاف پذیری، که با توجه به طرح پیکربندهای مسیر-هدایت برای جای دادن تعداد متغیر از AGVها تعریف می شود، به تدریج افزایش یابد و تاثیر آن بر عملکرد سیستم مورد بررسی قرار می گیرد تا بهترین پیکربندی را پیشنهاد دهد. جزئیات پیکربندی ها در بخش 4 مورد بحث قرار گرفته است. مسئله ازدحام AGV همانطور که پیشتر مورد بحث قرار گرفت (Rajotia و همکاران، 1998) از طریق یک خط مشی کنترل مناسب برای FMS حل می شود. همچنین، این مطالعه به منظور جستجوی عملکرد جهانی نزدیک به بهینه در هر پیکربندی گسترش یافته است و پیکربندی ها با بهترین عملکرد سیستم تولید مقایسه می شوند. این سیستم از طریق روش CPN مدل سازی می شود و روش سطح پاسخ (RSM) برای دستیابی به بهترین عملکرد سیستم پیاده سازی می شود. استفاده مشترک از CPN و RSM را می توان به عنوان یک روش کلی برای مدلسازی، تحلیل و بهینه سازی یک سیستم دینامیکی رویداد گسسته مورد استفاده قرار داد. علاوه بر این، این مطالعه, کاربرد ابزارهای پیشرفته مانند ابزارهای CPN و Expert Design را نشان می دهد و نشان می دهد که چگونه این ابزارهای قدرتمند را می توان برای مدلسازی، تحلیل و بهینه سازی یک سیستم تولید استفاده کرد.

3. شبکه رنگی پتری (CPN)

        یک سیستم تولید انعطاف پذیر, یک سیستم دینامیکی رویداد گسسته (DEDS) است که دارای ماهیت آسنکرون (ناهمگام)، موازی و رویداد-محور است. یک DEDS را می توان با وقایع و شرایط مشخص کرد، که می تواند به راحتی با روش شبکه پتری توصیف شود. در یک FMS، وقایع در یک روش موازی اتفاق می افتند که می تواند به صورت فشرده با روش رنگی شبکه پتری شبکه مدل سازی شوند. یک شبکه پتری شامل مکان ها، گذارها و قوس های جهتدار ارائه شده به ترتیب توسط دوایر، میله های مستطیلی و فلش ها می باشد. قوس ها بین مکان ها و گذارها اجرا می شوند. اماکن ممکن است هر تعداد از نشانه ها را داشته باشد. توزیع نشانه ها در مکان های یک شبکه نشانه گذاری می شود. مکان ها ممکن است شامل هر تعداد نشانه باشند. یک توزیع از نشانه ها روی مکان های یک شبکه, یک نشانه گذاری نامیده می شود. گذارها روی نشانه های ورودی توسط یک فرایند به نام شلیک کردن عمل می کنند. یک گذار در صورتی می تواند شلیک شود که توانمند شده باشد, یعنی, نشانه هایی در هر مکان ورودی وجود دارند. زمانی که یک گذار شلیک می شود, نشانه هایی را از مکان های ورودی خود مصرف می کند, برخی از وظایف پردازش را انجام می دهد و یک تعداد خاص از نشانه ها را در هر یک از مکان های خروجی خود قرار می دهد. یک ساختار شبکه پتری ساده در شکل 1 نشان داده شده است.

         شرایط یک DEDS به وسیله مکان ها توصیف می شود، رویدادها با گذارها توصیف می شوند، روابط بین رویدادها و شرایط توسط قوس ها توصیف می شوند و برقراری شرایط توسط نشانه ها در مکان ها توصیف می شوند. رخدادهای رویدادها بوسیله شلیک گذارها توصیف می شوند که نشانه ها را از مکان های ورودی حذف می کند و نشانه ها را به مکان های خروجی اضافه می کنند و رفتار یک سیستم توسط شلیک گذارها و حرکات نشانه ها توصیف می شود. برای تفسیر مناسب یک مدل, باید یک معنی به مکان ها، گذارها و نشانه ها اختصاص داده شود. در سیستم های تولید، به طور معمول مکان ها, منابعی مانند ماشین ها، مواد و غیره را نشان می دهند و وجود یک یا چند نشانه در یک مکان، نشان دهنده دسترسی به یک منبع خاص است، در حالی که عدم نشانه, نشان نمی دهد که این منبع در دسترس نیست. یک شلیک گذار نشان دهنده یک فعالیت یا عملیات فرآیند، به عنوان مثال، یک فرآیند ماشینکاری است. مکانها و گذارها با هم در شرایط عملیاتی سیستم، شرایط و روابط اولویت را نشان می دهند. شکل 2 یک مثال شبکه پتری از دیدگاه سیستم تولید را نشان می دهد.

Abstract

       The objective of this study is to model and maximize performance of an integrated Automated Guided Vehicle System (AGVS), which is embedded in a pull type multi-product, multi-stage and multi-line flexible manufacturing system (FMS). This study examines the impact of guide-path flexibility on system performance through the development of three different guide-path configurations which range from dedicated to flexible relationships between automated guided vehicles (AGVs) and machine/assembly station resources. The system is modelled using coloured Petri net method (CPN) and the simulation results lead to identify the resource redundancy which can be rectified to achieve lower overall cost of the system through the development of flexible guide-path configurations. The study is extended to seek global near-optimal conditions for each guide-path configuration using response surface method, which yields improvements in system throughput and cycle time along with a decrease in the numbers of AGVs.

1. Introduction

        In modern manufacturing environments, automated guided vehicle systems have become an integral part of overall manufacturing systems. An AGVS contains one or more automated guided vehicles which are driverless vehicles used for horizontal movement of materials. AGVs are commonly used in facilities such as manufacturing plants, distribution centres, warehouses and transhipments. The AGVS studied in this paper is a discrete event dynamical system (DEDS), i.e. a dynamic system with state changes driven by occurrences of individual events. This DEDS is event driven, asynchronous and non-deterministic in nature. Also, the considered AGVS is integrated with FMS and is interacting with flexible manufacturing/assembly system. Petri net are powerful techniques to model such systems in that they can handle complex system modelling concepts and constraints. Moreover, coloured Petri net (CPN) provides compact models of large systems with a higher level of abstraction (Desrochers & Al-Jaar, 1995). Hence, this study uses CPN method for modelling the system and the data generated by the CPN model are used to develop the response surface models to explore near-optimal conditions of the system.

2. Related work and originality

       Most machine scheduling research studies assume either that there are an infinite number of transporters for delivering jobs or that jobs are delivered instantaneously from one location to another without transportation time involved(Lee & Chen, 2001). The majority of the research work available in FMS modelling literature considers only the modelling of materials processing through work centres and assumes uninterrupted availability of material handling equipment. This could be valid for conveyorized production system but it is not reasonable for AGV-based systems (Tamer, Abdelmaguid, Ashraf, Kamal, & Hassan, 2004). Several researchers have stressed that efficient scheduling of material handling system is critical to the overall efficiency of FMS (Ulusoy & Bilge, 1993). The integration of material handling system (MHS) with manufacturing activities can result in manufacturing systems characterized by flexibility, high productivity and low cost per unit produced (Jawahar, Aravindan, Ponnambalam, & Suresh, 1998). Problems that address the optimal co-ordination of machine scheduling and job transporting are certainly more practical than those scheduling problems that do not take these factors into consideration. Also, to achieve global optimization between material processing and material handling activities, manufacturing planning should consider these two functions simultaneously (Seo & Egbelu, 1999). Nevertheless, the integration of MHS with FMS inevitably increases the complexity of a problem as it comprises inseparable decisions for both material processing and material handling activities (Lee & Chen, 2001). The earliest scheduling paper that explicitly considers the transportation factor is probably the one by Maggu and Das (1980). They considered a two-machine flow shop make-span problem with unlimited buffer spaces on both machines in which there are sufficient number of transporters so that whenever a job is completed on the first machine, it could be transported with a job-dependent transportation time, to the second machine immediately. Maggu, Das, and Kumar (1981) considered the same problem with the additional constraint that some jobs must be scheduled consecutively. Kise (1991) studied a similar problem but with only one transporter with a capacity of one and showed that the problem was NP-hard, even with job independent transportation times. Stern and Vitner (1990) considered a two-machine flow shop make-span problem where there is only one transporter with a capacity of one. They assumed that transportation times are job-dependent and that there is no intermediate buffer space at either machine. They formulated the problem as an asymmetric travelling salesman problem and gave a polynomial-time heuristic. Panwalker (1991) considered the same problem except that the buffer space at the second machine is infinite. He provided an optimal polynomial-time algorithm. The design and control processes of an AGVS involve many issues like (Vis, 2006):

• guide-path layout
• traffic management: prediction and avoidance of collisions and deadlocks

• number and location of pick-up and delivery points

• vehicle requirements

• vehicle-dispatching

• routing and scheduling

• positioning of idle vehicles

• battery management and failure management.

        Among these factors, guide-path or flow-path configuration design can be seen as a problem at strategic level (Le-Anh & De Koster, 2006). The guide-path layout influences the performance of a system as it impacts the travel time to transport a load from its origin to its destination, the number of vehicles required and the degree of congestion (Seo & Egbelu, 1999). The most common performance criterion in guide-path design is minimizing the total vehicle travel distance corresponding to given layout and flows (Gaskins & Tanchoco, 1987; Kaspi & Tanchoco, 1990). The direction of AGVs’ travel along guide-path may be unidirectional, bidirectional or a mix of unidirectional and bidirectional paths. Other developments in flow path design are single loops, tandem configurations and segmented flow configurations. The configuration of mixed unidirectional and bidirectional flow paths was studied in (Rajotia, Shankar, & Batra, 1998) with the purpose to reduce travel distance. It indicated that benefits could be obtained in throughput rates and in the size of vehicle fleet whereas the rate of vehicle congestion was increased and traffic control became more important. Gaskins and Tanchoco (1987) were one of the first to discuss the AGV guide-path layout problem with unidirectional arcs. The problem was presented as a network and formulated as a 0–1 integer linear programming model. The objective was to minimize the total transportation distance of AGVs. Kaspi and Tanchoco (1990) described a model with extra constraints and gave a computationally efficient procedure, namely branch and bound approach which was extended by Kim and Tanchoco (1993) by considering the fixed costs for construction, control and space of the system. Ko and Egbelu (2003) stated that in today’s dynamic production environment, changing product mixes and machine routes were realistic. They proposed and tested a heuristic for the design of AGV networks that could respond to changes in production volume and flow patterns. Asef-Vaziri, Laporte, and Sriskandarajah (2000) formulated the shortest loop design problem as an integer linear programming model. Bilge and Ulusoy (1995) considered an integrated production and material handling scheduling problem with the objective of minimizing the make-span in an FMS. Lee and DiCesare (1994) studied the integrated production and material handling scheduling in a job-shop context. A Petri net was presented and a heuristic method was proposed. The objective was to minimize the make-span. They considered a shop of three machines and one robot for transformation activities and five AGVs for material handling activities. Two cases were presented. In the first case, the AGV was dedicated to a job, accompanying it till the end of processing. In the second case, the AGV was dedicated to a machine to move the jobs after being processed by the machine. Two AGVs were dedicated to the load/unload station. (Sabuncuoglu & Hommertzheim, 1992a, 1992b) studied integrated scheduling of production and material handling for an FMS with a job-shop production environment. Simulation was used to evaluate the performance of scheduling rules. The objective considered was to minimize average flow time. The simulation methodology was used to model traditional, tandem and tandem/loop configurations in (Farling, Mosier, & Mahmood, 2001) and the benefits and limitations of each configuration was discussed. Aized, Takahashi, and Hagiwara (2007a) presented coloured Petri net based modelling and analysis of multiple products FMS with resource breakdown and automated inspection. This study did not address the issues related to material transportation and assumed an uninterrupted availability of dedicated automated guided vehicles. Aized, Takahashi, and Hagiwara (2007b) modelled and analysed an integrated automated guided vehicle system using coloured Petri net but this paper did not discuss any scheme for performance maximization considering multiple input factors simultaneously.

         In this study, an AGVS is integrated with an FMS and the interactions between FMS and AGVS are modelled and global system optimization is carried out using response surface method. The contribution of this study is that it analyses the impact of flexibility on the performance of an integrated AGVS through the development of different guide-path configurations. The configurations are developed in such a way that flexibility, defined in terms of guide-path configurations design to accommodate varying number of AGVs, is gradually enhanced and its impact on system performance is examined in order to propose the best configuration. The details of the configurations are discussed in Section 4. The problem of AGV congestion as discussed earlier (Rajotia et al., 1998) is solved through a suitable control policy for the FMS. Also, this study is extended to seek global near-optimal performance in each configuration and the configurations are compared to propose the best performance of the manufacturing system. The system is modelled through CPN method and response surface method (RSM) is implemented in order to achieve the best performance of the system. The joint use of CPN and RSM can be taken as a general methodology for modelling, analysis and optimization of a discrete event dynamical system. Moreover, this study presents the application of advanced tools like CPN Tools and Design Expert and shows how these powerful tools can be used to model, analyse and optimize a manufacturing system.

3. Coloured Petri net (CPN)

       A flexible manufacturing system is a discrete event dynamical (DEDS) system, which is asynchronous, parallel, and event driven in its nature. A DEDS can be characterized by events and conditions, which can be described by Petri net method easily. In an FMS, events are occurring in a parallel way that can be modelled compactly by coloured Petri net method. A Petri net consists of places, transitions and directed arcs represented by circles, rectangular bars and arrows, respectively. Arcs run between places and transitions. Places may contain any number of tokens. A distribution of tokens over the places of a net is called a marking. Transitions act on input tokens by a process known as firing. A transition can fire if it is enabled, i.e., there are tokens in every input place. When a transition fires, it consumes the tokens from its input places, perform some processing task and places a specified number of tokens into each of its output places. A simple Petri net structure is shown in Fig. 1.

       The conditions of a DEDS are described by places, events are described by transitions, relations between events and conditions are described by arcs and holding of conditions are described by tokens in places. The occurrences of events are described by firing of transitions which remove tokens from input places and add tokens to output places and the behaviour of a system is described by firing of transitions and movements of tokens. Places, transitions and tokens must be assigned a meaning for proper interpretation of a model. In manufacturing systems, normally places represent resources like machines, materials etc. and the existence of one or more tokens in a place represents the availability of a particular resource, while no token indicates that the resource is unavailable. A transition firing represents an activity or process execution, for instance, a machining process. Places and transitions together represent conditions and precedence relationships in a system’s operation. Fig. 2 shows a Petri net example from manufacturing system point of view.

چکیده

1. مقدمه

2. کار مرتبط و منشا

3. شبکه رنگی پتری (CPN)

4. پیکربندی سیستم تولید انعطاف پذیر

4.1 پیکربندیهای AVGS

5. خط مشی کنترل

6. توسعه مدل

6.1 مدلسازی CPN

6.2 مدلسازی سطح پاسخ

7. نتایج شبیه سازی و بحث و بررسی

7.1 معیارهای عملکرد

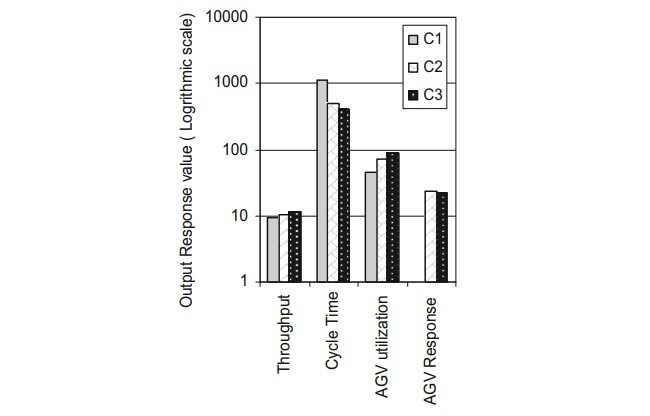
7.2 تاثیر پیکربندیهای مسیر-هدایت روی کارایی و زمان چرخه

7.3 تأثیر پیکربندی های مسیر-هدایت در کاربرد AGV

7.4 تاثیر پیکربندیهای مسیر-هدایت روی زمان پاسخ AGV

7.5 ازدحام AGV

8. جستجو برای یک AGVS بهینه

8.1 راه حل های ماکزیمم عملکرد

9. نتیجه گیری

منابع

Abstract

1. Introduction

2. Related work and originality

3. Coloured Petri net (CPN)

4. Flexible manufacturing system configuration

4.1. AGVS configurations

5. Control policy

6. Model development

6.1. CPN modelling

6.2. Response surface modelling

7. Simulation results and discussion

7.1. Performance measures

7.2. The impact of guide-path configurations on throughput and cycle time

7.3. The impact of guide-path configurations on AGV utilization

7.4. The impact of guide-path configurations on AGV response time

7.5. AGV congestion

8. Search for an optimal AGVS

8.1. The maximum performance solutions

9. Conclusion

References