دانلود رایگان مقاله بهینه سازی لیآپ در برابر کمانش پانل های برشی

چکیده

      هدف از این مطالعه, بهینه سازی بار کمانش برشی صفحات کامپوزیت ورقه ورقه شده بود. این ورقه ها فاقد تزویج بین خمش و انبساط   بودند، اما در غیر این صورت انتخاب دلخواهی از تغییر زاویه لایه در ضخامت داشتند. صفحات, مستطیل شکل بودند و یا به سادگی در تمام لبه ها پشتیبانی و یا محکم می شدند. برای صفحات ناهمسانگرد، دیده شد که تنها یک پارامتر لازم برای پیداکردن طراحی بهینه در مواد مختلف و نسبت های صفحه وجود دارد. این پارامتر را می توان به عنوان زاویه لیآپ در یک چندلایی (+/- θ) ناهمسانگرد تفسیر نمود. هنگامی که تزویج خمشی-پیچشی وجود دارد، قدرت کمانش به جهت بار اعمال شده بستگی دارد. یک چند لایی با سختی های تزویج خمشی-پیچشی غیر صفر را می توان با چهار پارامتر ورقه ورقه سازی توصیف نمود. ناحیه مجاز این پارامترها مورد بررسی قرار گرفت و بهینه سازی بار کمانش در این ناحیه انجام شد. دیده شد که حتی این مسئله تک پارامتری است. این پارامتر را می توان به عنوان  زاویه  لیآپ θ در یک چندلایی تک سویه خارج از محور (θ) تفسیر نمود.

1. مقدمه

      وظیفه بهینه سازی لیاپ صفحات ورقه ورقه شده به منظور حداکثرسازی بارهای کمانش برشی درون-صفحه به طور گسترده مطالعه نشده است. اولین ملاحظه در مورد این مسئله, توسط Hausner and Stein (1975), بود که زاویه را در یک چندلایی زاویه-لایه دارای محور اصلی عمودی بهینه سازی نمودند. Hirano 1979, آزادی بیشتری را در انتخاب لیاپ مجاز نمود, اما  غیرهمسانگردی را نادیده گرفت (تزویج خمش-کمانش). نتیجه این مطالعه این بود که چندلایی های زاویه-لایی بهینه هستند و داده های ارائه شده توسط Housner و Stein معتبر باقی ماندند.

       Thielemann (1950) نشان داد که سختی های تزویج خمش-پیچش (D16,D26) به این حقیقت منجر می شود که یک صفحه با یک نسبت صفحه نامتناعی, به جهت ارجح برشی می رسد. در یک جهت, قدرت کمانش برشی, برای چندلایی دارای محور اصلی عمودی متناظر بالاتر در در جهت دیگر, پایین تر است.

      هیچ بررسی از لیاپ بهینه برای چندلایی های غیرناهمسانگرد یافت نشده است, حتی با اینکه مشخص است که چنین صفحاتی دارای مقاومت های کمانش برشی بالاتر هستند (اما در یک جهت). مقاله حاضر, به مطالعه این مسئله می پردازد. دیده می شود که بهینه سازی کمانش برشی, یک مسئله تک پارامتری است. نتایج مشابه برای بهینه سازی فرکانس ارتعاش, کمانش فشردگی تک محوره انحراف تحت یک فشار ثابت حاصل شده اند  .

2.پیکربندی های صفحه و چندلایی

      صفحات در نظر گرفته شده در این مقاله, مستطیلی با اندازه a*b به ترتیب در جهات x و y و با ضخامت ثابت h بودند. لبه ها, همه به سادگی در مورد تغییر شکل خارج از صفحه پشتیبانی و محکم شده اند. مواد استفاده شده در این مطالعه در جدول 1 ارائه شده اند. چندلایی های در نظر گرفته شده توسط یک ماتریس کامل از سختی های خمشی مشخص می شوند, اما بدون تزویج بین خمش و انبساط. تحت این محدودیت ها, هر انتخاب از تغییر زاویه لایه از طریق ضخامت مجاز است. چندلایی های متقارن, این شرایط را برآورده می سازند, اما چندلایی های دیگری نیز وجود دارند که آنها را برآورده می سازند. تنش های پیش-کمانش روی صفحه ثابت هستند, بنابراین سختی های درون-صفحه Aij بر تنش های کمانش تاثیر نمی گذارند. به دلیل این مورد و فقدان تزویج انبساط-خمش, معادلات دیفرانسیل تعادلی حاکم را می توان باز نمود و معادله برای تغییر شکل خارج از صفحه برای ارائه بار کمانش برشی حل می شود.

       فرض می شود که صفحات در نظر گرفته شده در این مقاله حاضر, مفروضات کرشف-لاو را برآورده می سازند, یعنی اثر تغییر شکل برشی عرضی نادیده گرفته می شود. این می تواند به خطاهای معنادار منجر شود, اگر یک طول مشخصه درون صفحه, مثلاً طول موج کمانش, در همان مرتبه ضخامت صفحه باشد. علاوه بر این, اثر تغییر شکل برشی عرضی زمانی افزایش می یابد که نسبت ها بین ماژول برشی عرضی و ماژول درون صفحه چندلایی کاهش یابد. برای مواد FRP عادی, چنین نسبتی می تواند در مرتبه 1:50 باشد.  , یک مثال را ارائه نمود که در آن تئوری کلاسیک صفحه, بار کمانش را با 40% برای یک صفحه با نسبت ضخامت-به-عرض 0.05 دست بالا گرفت. بر این اساس, چون FRP, در اینجا در نظر گرفته شده اند, تحلیل کنونی تنها باید برای چندلایی هایی به کار رود که در مقایسه با طول های مشخصه درون صفحه بسیار نازک هستند.

4. روشی برای محاسبه بارهای کمانش

      برای محاسبه بارهای کمانش برشی, یک کد تفاضل متناهی پیاده سازی شد که منجر به معادله ماتریس زیر است  (A -- N.yB) w = 0, که یک مسئله مقدار ویژه نامتقارن تعمیم یافته است. این معادله با استفاده از روش های عددی استاندارد حل شد. مقایسه نتایج این رویکرد با داده های ارائه شده در نوشته ها برای صفحات مربعی نشان داد که خطا کمتر از 1% است. برای دیگر نسبت های صفحه, گسسته سازی, ریزتر شد, اما خطا این نسبت های صفحه فرضاً برای صفحات مربعی بزرگتر بود.

5. بهینه سازی و نتایج, چندلایی های ناهمسانگرد

      فقط دو پارامتر,  w1 و w2  مورد نیاز برای توصیف چندلایی های ناهمسانگرد وجود دارند. برای نسبت های صفحه ab = 1.0,1.3,1.7,2.0,2.5,3.0,4.0 و نامتناهی, بار کمانش به ازای پارامترهای ورقه ورقه کردن ترسیم شد. شکل 2, یک نمونه از چنین نموداری است. به علت شرایط مرزی متقارن, صفحات با نسبت های صفحه a/b کمتر از یک, معادل صفحات با نسبت صفحه b/a است. برای صفحه با نسبت صفحه نامتناهی, داده های   استفاده شد. برای هر نمودار, 137 بار کمانش برای مقادیر مختلف پارامترهای ورقه ورقه سازی محاسبه شدند. همانطور که در شکل دیده شد, ماکزیمم بار کمانش در مرز ناحیه مجاز پارامترهای ورقه ورقه سازی مشخص می شود. همین مورد برای تمام نسبت های صفحه, تمام مواد, برای لبه های حمایت شده ساده و محکم شده دیده شد. این حقیقت به نظر می رسد که تنها یک پارامتر مورد نیاز برای بهینه سازی کمانش برشی صفحات مستطیلی ناهمسانگرد وجود دارند. این پارامتر را می توان به عنوان زاویه لیاپ   در یک چندلایی ناهمسانگرد توصیف نمود. این, نتایج   را تایید می کند و داده های ارائه شده توسط  , معتبر می ماند.

 6. بهینه سازی و نتایج, چندلایی های همسانگرد

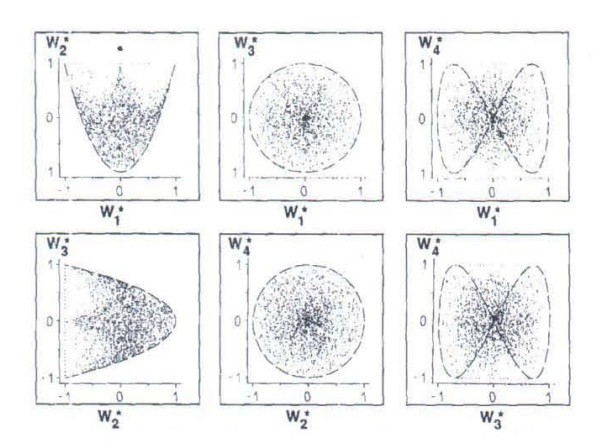
      هنگامی که تزویج خمشی-پیچشی در چندلایی حاضر است, تمام چهار پارامتر ورقه ورقه شدن نیاز می شوند. یک روال عددی استاندارد برای وظیفه یافتن طراحی بهینه در نسبت های صفحه ab= 1.0, 1.2, 1.5, 1. 7, 2.0, 2.5, 3.0   با پارامترهای ورقه ورقه سازی محدود شده توسط شش تصویر دوبعدی از ناحیه مجاز   تا   استفاده شد. این به یک ناحیه بسیار بزرگ منجر می شود و ممکن است که نقطه بهینه یافت شده تحت این شرایط قابل تحقق فیزیکی نباشند. هرچند, بهینه سازی انجام شد و دیده شد که طرح های بهینه همیشه نزدیک به منحنی های متناظر با ورقه های تک جهتی خارج از محور روی شش تصویر ناحیه مجاز یافت می شوند. شکل 3, یک نمونه از این مورد است. در جدول 2, نقاط بهینه برای صفحات پشتیبانی شده ساده با ورقه های تک جهتی خارج از محور مقایسه شده اند.

Abstract

      The object or the study wu to optimiZI: the shear buckling 19ad of laminated compoaite plates. The laminates lacked coupling between bendiDg and extension (E ij:O) but had otherwise arbitrary selection of the ply anslt variatKlO through the thickness. The platea were rectangular and either simply supported or c1a.mped on all edges. For (,rthotropic plates, it was seen that there is only one parameter llecessary ror findin g the optimal design for different materials an i plate a&- pect rati08. This parameter can be interpreted r..a the layup angle 8 in a (+/- 6) orthotropic laminate. Wh ~JL bendingtwisting coupling is preaent, the buckling strength i. epends on the direction of the applied load. A laminate wib non-zero bending-twisting coupling st rrn~es can be described with four lamination parametera. The allowable region of tbe:1e parameters was investigated, and an optimization of the budling load within this region was perrormed. It wu seen that nen thiA i! a one parameter problem, This parameter can be interpreted as the layup anlge 8 in an off-&X.il!!l unidirectiollallarr.inate (8).

1. Iutroduction

       The task of optimizing the layup of laminated plates in ord,'r to maximize in-plane shear buckling loads has not beeH studied extensively. The first trea.tment oC the prolr lem was probably by Hausner and Stein (1975), who optimized the angle in an orthotropic. angle-ply laminate. Hiranu (1979) a.llowed more freedom in the choice of layup, but still neglected anisotropy (bending-twisting coupling). The conclusion from this study was that angle-ply laminah-s are optimal, and the data presented by HouBner and Stei ll remained valid.

      Thielemann (1950) showed that non-zero bendingtwisting coupling stifi'ncsses (D16 , D26) results in the fact tha.t a plate with an infinite aspect ratio gets a preferred dire:tion of shear. In one direction, the :shear buckling stJe:lgth is higher than ror t.he corresponding orthot ropic lamma.te, in the other it is lower.

       No investigation of the optimal layup for non-orthotropic laminates h88 been found , even though it is c1ea.r t hat such plates have higher shear buckling strengths (but only in one direction). The pn:sent article studies this prQ\,iem. It is seen that shear buckling optimization is a or. e parameter problem. Similar results have been obtain d ror the optimization of vibration frequency, uniaxial compression buckling, and deflection under a constant pres,ure (Grenestedt 1990).

2. Plate and laminate configurations

       The plates considered in this article are rectangular or the size a * b in the z and y directions, respectively, and with the constant thickness h. The edges are either all simply s,upported or clamped concerning the Qut-of ·plane deformation.. The materials used in the study a.r ~ given in Ta.ble 1. The laminates considered are characl,erized by a full matrix of bending stiffnesses, but withou'; coupling between bending and extension. Under these re!trictiollS, any choice of ply angle variation through the thickness is allowed. Symmetric laminates fulfil these req1lirements, but there are also other laminates that fulfil them. The pre.buckling stresses afe constant over the plate, so the in-plane stiffnesses ~i do not affect the buck1in~ stresses. Because of this and the lack of bending-exteMion coupling, the governing equilibrium differential equatiofUI can be de-- coupled, and the equation for the out-of-plane deformation is solved to give the shear buckling load.

       The plates considered in the present papel are supposed to satisfy the Kirchoff-Love assumptions, i.e. the effect of transverse shear deformation is negleded. This might lead to significant errors if a characteristi: in-pla.ne length, e.g. the buckling wave length, is of the n,me order as the plate thickness. Furthermore, the effed of transverse shear deformation increases when the ratios between transverse shear moduli and in-plane moduli of the laminate decrease. For ordinary FRP materials su·:h a ratio might be in the order of 1:50. Cohen (1982) presented an example where the classical plate theory overestimated the buckling load with 40% for a plate with a thickn ...  to-width ratio of only 0.05. Accordingly, .ince FRP are considered here, the present analysis should or.ly be applied to laminates which are very thin compmed to the characteristic in-plane lengths.

4. Method for calculating the buckling loads

      For calculation of the shear buckling loads, a numerical finite difference code was implemented, resulting in the matrix equation (A -- N.yB) w = 0, (9) whl<h is a generalized nonsymmetric eigenvalue problem. It was solved using standard numerical methods. Compari:1g the results of this approach with data presented in the literature for square plates revealed that the error was less than 1%. For other aspect ratios, the discretization was made finer, but supposedly the error for these aspect ratic'LS was larger than (or the square plates.

5. Optimitation and results, orthotropic laminates

      There are only two parameters, W1 and W2 needed for desclibing the orthotropic laminates. For the aspect ratios ab = 1.0,1.3,1.7,2.0,2.5,3.0,4.0, and infinity, the buckling load was plotted versus the lamination parameters. Figure 2 is an example o( such a plot. Because of the sYIOJnetric boundary conditions, .plates with aspect ratios alb HmalJer than unity is equivalent to plates with the aspect ratio bl a. For the plate with infinite aspect ratio the data of Seydel (1933) was used. For each plot, 137 buckling loads for different values of the lamination parameters were calculated. ~ seen in the figure , the maximal buck-ling loa.d is found on the border of the allowa.':>le region of the lamination parameters. The same waa 81!en for all aspect ratios, all materia.ls, for both simply supported a.nd clamped edges. It appea1'1l to be the fact that th,,,e is only one parameter needed for the shea.r buckling op;;imization of orthotropic rectangular plates. This para.met,er can be interpreted as the layup angle 9 in an orthotrop.c (+/- 9) laminate. This confirms the results of Hirano (HI79), and the data presented by Housner and Stein (1975) remain valid.

6. Optimization and results, non-orthotropic laminates

      When bending-twisting coupling is present in the lamiDc.tl!, all of the four lamination parameters are needed. A standard numerical routine was used for the task of finding the optimal design for the aspect ratios ab= 1.0, 1.2, 1.5, 1. 7, 2.0, 2.5, 3.0 and 4.0, with the lamination parameters conBtrained by the six two-dimensional projectioll8 of the allowable region of Wi to W:. This results in a too big regior. and it is possible that the optimal point found under such conditions cannot be realized physically. However, the optimization was carried out and it was seen that the optimal designs always were found very close to the curves corresponding to off-axis unidirectional laminates on the six >rojections of the allowable region. Figure 3 is an exaIDl,le of this. In Table 2 the optimal points for simply sup:)orted plates are compared with off-axis unidirectional laminates. The difference might be due to numerical errors - the vicinity of the optimal point is very flat so it is difficult to find the optimal point with good accuracy, even if the optimal buckling load could be determined with good pre<ision - but it is suspected that the true optimum alwaY-I is an off-axis unidirectional laminate. However, this has not been proved analytically.

چکیده

نمادها

1. مقدمه

2.پیکربندی های صفحه و چندلایی

3.پارامترهای ورقه ورقه کردن و ناحیه مجاز آنها

4. روشی برای محاسبه بارهای کمانش

5. بهینه سازی و نتایج, چندلایی های ناهمسانگرد

6.بهینه سازی و نتایج, چندلایی های همسانگرد

Abstract

1.Iutroduction 

2. Plate and laminate configurations

3. Lamination parameters and their allowable region 

4. Method for calculating the buckling loads 

5. Optimitation and results, orthotropic laminates 

6. Optimization and results, non-orthotropic laminates