دانلود رایگان مقاله مشاهده حالت بهینه با استفاده از محدودیت درجه دوم

        این مقاله، طرح یک مشاهده گر حالت را ارائه می دهد که محدودیت درجه دوم خطای تخمین را تضمین می نماید. با استفاده از تجزیه و تحلیل پایداری تابع لیاپانوف درجه 2، سرعت همگرایی و بیضی محدود کننده خطای نهایی (حالت پایدار) به صورت پارامترهایی مشخص می شوند که رفتار تخمین را تعریف می نمایند. سپس، نشان داده شده است که این اهداف می تواند در یک تابع مقیاس پذیر با یک پارامتر طراحی ادغام شود که این باعث ایجاد مسأله طراحی محدب می گردد. در بخش دوم این مقاله، یک مدل UAV (پهپاد) ارائه شده است که می تواند با در نظر گرفتن یک حالت ویژه و یک چارچوب داوری، به صورت خطی ساخته شود. مدل UAV برای ترکیب یک الگوی آشفتگی با اندازه متغیر گسترش یافته است. مدل مشترکی که با دنبال کردن خطوط رویکرد طراحی پیشنهادی، مطابق با ساختار مورد نیاز برای استخراج یک ناظر (مشاهده گر) می باشد. مشاهده گر آشفتگی، اقدامات UAV را استخراج کرده و تجزیه و تحلیل عملکرد مربوط به آن را با توجه به پارامترهای طراحی ارائه می دهد. اثربخشی و خصوصیات اصلی رویکرد پیشنهادی با استفاده از نتایج شبیه سازی نشان داده شده است. 

1. مقدمه

        مسأله مشاهده حالت در کنترل بسیار مهم است، زیرا در بسیاری از سیستم های کنترل متغیرهای حالت به دلیل محدودیت های فیزیکی یا اقتصادی برای اندازه گیری، در دسترس نیستند. به همین دلیل، چندین اثر در مقالات، بر طراحی برآوردگرهای حالت متمرکز شده اند (به عنوان مثال، زیتز ، 1987؛ گریپ و همکاران ، 2012؛ ژانگ و همکاران ، 2012b؛ چادلی و کریمی ، 2013؛ روتوندو و همکاران ، 2016؛ حسنی و همکاران ، 2017).

         از جمله رویکردهایی که در سالهای اخیر مورد توجه جامعه کنترل قرار گرفته است، مواردی است که مبتنی بر محدودیت درجه دوم (QB) می باشد. به طور کلی، QB به تضمین محدودیت کلیه مسیرهای حالت یک سیستم با استفاده از یک تابع لیاپانوف درجه 2 اشاره دارد. این مفهوم ابتدا برای سیستمهای غیرخطی توسط بروکمن و کولس (1995) معرفی شده و سپس به سیستم های خطی به صورت اسمی نیز گسترش یافته است (بروکمن و کولس، 1998). از آن زمان تاکنون، چندین نتیجه از این مفهوم به منظور برآورد حالت، مورد بهره برداری قرار گرفته است. به عنوان مثال، الساندری و همکاران. (2004) از QB برای مقابله با ثبات و طراحی برآوردگرهای افق پیش بین استفاده کرده اند. الساندری و همکاران. (2006)، QB را برای طراحی برآوردگرهای حالت برای سیستم های خطی زمان گسسته با عدم قطعیت چند وجهی نیز به کار برده اند و این کار توسط ژانگ و همکاران (2012a) بیشتر توسعه یافته است، آنها آشفتگی های حالت و نویز اندازه گیری را به طور مستقل در نظر گرفته اند. 

         جالب است که QB برای حل مسائل مربوط به تثبیت بازخورد خروجی (دینگ، 2009، 2013؛ دینگ و پن، 2016؛ پینگ و همکاران، 2017؛ پینگ، 2017)، کنترل تحمل خطا (ویچاک و همکاران، 2016) و برآورد خط (بوسیاکوفسکی و همکاران، 2017a، 2017b؛ ویچاک و همکاران، 2017) نیز به کار می رود. اخیراً، توسعه هایی بیشتری از مفهوم QB مورد بررسی قرار گرفته است؛ به عنوان مثال، به محدودیت های غیر درجه دو بسط یافته معرفی شده توسط زوو و لی (2011)، مراجعه فرمایید.

        یک موضوع مرتبط که برای چندین سال به طور گسترده مورد بررسی قرار گرفته است، طراحی مشاهده گرهای آشفتگی می باشد. ایده این است، هنگامی که یک تخمین آشفتگی در دسترس باشد، می توان یک اقدام کنترلی برای جبران تأثیر این آشفتگی به دست آورد، این ایده، کنترل مبتنی بر مشاهده گر آشفتگی (DOBC) را به وجود آورد که به طور گسترده توسط چن و همکاران مورد بررسی قرار گرفته است. از دهه 1960، تکنیک های مختلفی برای به دست آوردن تخمین آشفتگی پیشنهاد شده است، مانند مشاهده گرهای ورودی ناشناخته (جانسون، 1971)، مشاهده گرهای آشفتگی (کوون و چونگ، 2003)، برآوردگرهای مبتنی بر آشفتگی ورودی معادل (شی و همکاران، 2008)، مشاهده گرهای حالت تعمیم یافته (لی و همکاران، 2012)، مشاهده گرهای آشفتگی (چین و همکاران، 2000) و فیلترهای تاکاگی-سونگنو فازی (چیبانی و همکاران، 2017).

       مقابله با پویایی های مربوط به آشفتگی های مدلسازی نشده، یک مسئله مهم و اساسی در کنترل وسایل نقلیه هوایی بدون سرنشین (پهپاد) است. در برخی از محیط ها، کنترل پهپادها یک کار بسیار چالش برانگیز است، از آنجا که هر کنترل کننده ای که آشفتگی ها را در نظر نمی گیرد، ممکن است منجر به یک رفتار ناخواسته، از اختلال در عملکرد گرفته تا بی ثباتی، گردد. به همین دلیل، علاقه زیادی به استفاده از DOBC در پهپادها وجود دارد. به عنوان مثال، روگیرو و همکاران (2014؛ 2015)، تکنیک های تخمین آشفتگی را با استفاده از یک مدل غیر خطی همراه با تکانه تعمیم یافته به عنوان یک حالت به کار بردند. در این مقالات، معادلات جبری شامل اختلال و مشتقات ناشناخته حالت به دست آمده و تخمین آشفتگی می باشد که با تغذیه انتگرال معادلات جبری به فیلتر مرتبه دوم بدست می آید. از طرف دیگر، یوکسل و همکاران. (2014) مشاهده گر اختلال (آشفتگی) غیر خطی را بر اساس معادلات غیر خطی حرکت که از سرعت و شتاب به عنوان حالت استفاده می نماید، بدست آوردند. پایداری مشاهده گر در مورد بروز اختلالات ثابت خارجی (مشتق تهی) و عدم نویز نشان داده می شود. توجه داشته باشید که اثربخشی آثار فوق، یا با استفاده از سنسورهای داخلی، که اندازه گیری های بسیار دقیقی از موقعیت و سرعت ارایه می دهد و یا با در نظر گرفتن سناریوهای شبیه سازی بدون نویز نشان داده شده است. در عین حال، آنها این فرضیه را به اشتراک می گذارند که این اختلال متغیر است و ممکن است باعث اختلال در عملکرد واقعی پهپادها شود.

         سهم اصلی این مقاله، طراحی مشاهده گرهای درجه دوم با در نظر گرفتن وجود یک معامله بین نرخ همگرایی و خطای نهایی (حالت پایدار) محدود کننده بیضوی است. به منظور دستیابی به هر دو هدف، یک تابع هدف مقیاس پذیر با یک پارامتر طراحی ساخته شده است، به گونه ای که این خود باعث ایجاد مشکل طراحی محدب می شود. روش طراحی به دست آمده تضمین می کند یک معامله بهینه (مطلوب) بین رفتارهای گذرا و بدون علامت، مطابق با کار الساندری و همکاران (2006) وجود دارد، اما از دو جنبه مهم با آن متفاوت است. ابتدا به جای به حداقل رساندن کران بالای خطای نهایی، حجم بیضی که خطا در آن قرار دارد به حداقل می رسانیم که منجر به به حداقل شدن راه حل های خطا می گردد. دوم، در حالی که کل تخمین حالت برای همگرایی به حالت واقعی تضمین شده باشد، روش طراحی پیشنهادی به کاربر این امکان را می دهد بخشی از حالت را انتخاب کند که خطای تخمین مرتبط با آن به حداقل رسیده باشد، و راه حل های محکم تری برای قسمت خاصی از حالت ارایه نماید. این واقعیتها باعث می شود رویکرد پیشنهادی با سایر تکنیک های توسعه یافته برای طراحی مشاهده گر متفاوت باشد، مانند روش های مبتنی بر بهینه سازی H (وانگ و همکاران، 1999؛ عباس زاده و مارکز، 2009) یا مفهوم پایداری ورودی به حالت (ISS) (الساندری، 2004؛ 2013)، که صریحاً حجم خطای بیضوی حالت پایدار را به حداقل نمی رساند.

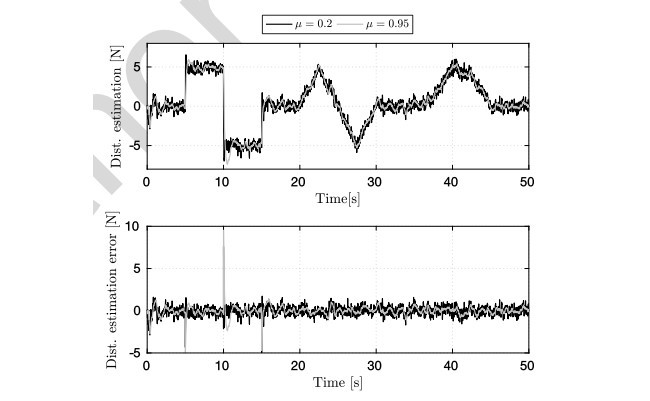
        روش پیشنهادی برای مسئله تخمین اختلالات پهپادها بکار رفته و از نتایج شبیه سازی برای نشان دادن اثربخشی و خصوصیات اصلی آن استفاده شده است. به ویژه، نشان داده شده است که مدل UAV می تواند به شکل خطی از طریق انتخاب مناسب متغیرهای حالت (تکانه خطی و چرخشی) و قاب مرجع (جهان اول) بیان شود. سپس، مدل UAV با استفاده از یک مدل آشفتگی (اختلال) مرتبه بالا توسعه داده می شود، همانطور که توسط کیم و همکاران (2010)، گادبول و همکاران (2013) و سو و همکاران (2015) ارایه شده است. مدل کلی یک سیستم خطی است که با ساختار مورد نیاز مشاهده گر درجه دوم کران دار پیشنهادی مطابقت دارد. این مدل با ساخت و ساز ، اندازه گیری های بدست آمده از سنسورهای آن بورد (on-board) پس از یک فرایند فیلترینگ مناسب مطابقت دارد و پویایی های اختلال را محدود نمی سازد. با این حال، این اجازه می دهد تا اطلاعات مربوط به ماهیت اختلالات به ترتیب مشتق مورد نظر وارد شود. شایان ذکر است که به دلیل مدل خاص آشفتگی، مشاهده گر طراحی شده یک عمل متناسب چند جانبه (PMI) را در نظر می گیرد که کاربرد روش طراحی در ساختارهایی مانند مواردی که توسط بوسون و کابور (2001) یا کونیگ (2005) در نظر گرفته اند را نشان می دهد. 

          این مقاله به شرح زیر سازماندهی شده است. اول، در بخش 1 نماد استفاده شده در طول مقاله ارائه می شود. سپس، نحوه بدست آوردن روش بهینه طراحی ناظر (مشاهده گر) را نشان داده می شود. در بخش 3، مدل UAV به دست آمده است. بخش 4 نتایج استفاده از مشاهده گر به دست آمده برای مدل UAV را نشان می دهد. در نهایت، نتایج در بخش 5 ارایه می شود.

          This paper presents the design of a state observer which guarantees quadratic boundedness of the estimation error. By using quadratic Lyapunov stability analysis, the convergence rate and the ultimate (steady-state) error bounding ellipsoid are identified as the parameters that define the behaviour of the estimation. Then, it is shown that these objectives can be merged in a scalarised objective function with one design parameter, making the design problem convex. In the second part of the article, a UAV model is presented which can be made linear by considering a particular state and frame of reference. The UAV model has been extended to incorporate a disturbance model of variable size. The joint model matches the structure required to derive an observer, following the lines of the proposed design approach. An observer for disturbances acting on the UAV is derived and the analysis of the performances with respect to the design parameters is presented. The effectiveness and main characteristics of the proposed approach are shown using simulation results.

1. Introduction

         The problem of state observation is very relevant in control, since in many control systems the state variables are not accessible for measurement due to either physical or economical limitations. For this reason, several works in the literature have focused on the design of state estimators, (see, e.g., Zeitz, 1987; Grip et al., 2012; Zhang et al., 2012b; Chadli and Karimi, 2013; Rotondo et al., 2016; Hassani et al., 2017).

1. مقدمه
2. مشاهده گر (ناظر) کران دار (محدود) درجه دوم بهینه
2.1 طراحی مشاهده گر (ناظر) حالت
3. معادلات پویای UAV
3.1 معالات حرکت پویا
3.2 مدل آشفتگی (اختلال)
3.3 مدل گسترش یافته با توجه به آشفتگی ها
3.4 اندازه های سیستم
4. مشاهده گر کران دار (محدود) درجه دوم بهینه UAV
5. نتیجه گیری
منابع

1. Introduction
2. Optimal quadratic boundedness observer
2.1. State observer design
3. UAV dynamic equations
3.1. Dynamic motion equations
3.2. Disturbance model
3.3. Extended model considering disturbances
3.4. System’s measurements
4. UAV optimal quadratic boundedness  observer
5. Conclusions
References