دانلود رایگان مقاله قوانین مقیاس بندی و شهر مدرن

چکیده

      تجزیه و تحلیل روابط درونی و پیچیدگی فضاهای شهری مدرن به منظور میسر نمودن بهبود شرایط زندگی و یا کمک به تعیین تصمیمات بهینه به منظور صرفه جویی در انرژی و یا بهبود پایداری, امری مشکل است. تصمیمات و رهنمودهای به دقت طراحی شده ممکن است به دلیل خصوصیات و یا مجموعه های پیچیده از واکنش ها از ساکنان و یا همتایان اقتصادی, نتایج غیر منتظره را تولید کنند. مثلاً زمانی که خدمات مایل به تمرکز روی تراکم های بزرگ هستند و نیازهای حمل و نقل دارای اهمیت حیاتی می شوند, پیچیدگی با اندازه افزایش می یابد. مبرهن است که سیستم های پیچیده مانند موجودات زنده به دنبال روابط تقریبی مانند قوانین مقیاس بندی بین متغیرهایی هستند که آنها را توصیف می کنند. برخی از این نوع روابط در رابطه با فضاهای شهری توسعه یافته مدرن آزمایش می شوند که در آن, پیدا کردن یک تداوم منطقی با انواع مقیاس ها در موجودات زنده امکانپذیر است و برخی از نتایج اولیه استنتاج می شوند.

1. مقدمه

      شهرهای بزرگ, درجه بالایی از پیچیدگی و روابط درونی قوی را میان ساکنان و محیط اطراف خود دارند. امروزه به نظر می رسد درجه پیچیدگی و این روابط درونی, شرایط مطلوب، و یا شرایط زندگی بهتر را با افزایش اندازه و تعداد شهرهای بزرگ ایجاد می کنند. به دلیل طیف وسیعی از پیش بینی ها که باید در نظر گرفته شوند, برنامه ریزی شهری در شهرهای بزرگ یک چالش دشوار است. این امر در صورتی می تواند بسیار جذاب باشد که قوانین طبیعی وجود داشته باشند که رشد هدایت شود و یا حداقل شرایط مطلوب را به همراه داشته باشند. با این حال، روابط دقیق فیزیکی بین متغیرهایی که این شرایط را تعیین می کنند, با توجه به پیچیدگی سیستم و مجموعه های متعددی از متغیرهای مورد نیاز برای توصیف آن، که با هم به عنوان یک سیستم فیزیکی در نظر گرفته می شوند بسیار پیچیده هستند. با این وجود، به نظر می رسد برخی از ایده ها و گرایش ها بین بسیاری از شهرهای مدرن مشترک هستند: باید مواردی چون هزینه های انرژی، حمل و نقل کالاها (از جمله غذا، آب، ...)، حمل و نقل عمومی و خصوصی، و مسائل مربوط به آلودگی را بهینه سازی نمود. بنابراین انتظار برخی از روندهای عمومی (اگر نه, « قوانین» دقیق) که شهرهای مدرن باید از آن پیروی نمایند منطقی است و تفکر در مورد آن به عنوان سیستم های فیزیکی و پیچیده قابل قبول است.

       بنابراین، ما باید از روابط پدیدارشناختی در سیستم های موجود پیچیده ای است که طی هزاران سال تکامل یافته اند درس بگیریم. همانطور که موجودات زنده یکی از این سیستم ها را نشان می دهند که تا حد زیادی مورد مطالعه قرار گرفته اند، و در واقع یک الگو از پیچیدگی هستند، مطالعه قوانین کلی و یا روابط عمومی در زیست شناسی می تواند بیشنشی را نسبت به مشکل ما ارائه دهد. در واقع این حدس معقول و منطقی به نظر می رسد که رفتار کلان سیستم های زنده ممکن است از قوانین جهانی قابل سنجش پیروی نماید که ویژگی های ضروری سیستم را در بردارد, همانطور که مرجع [1] نشان می دهد.

      مقیاس بندی، به عنوان مظهر پویایی و هندسه کلی اصلی، در سراسر فیزیک مشهود است. این مقوله به دانشمندان در به دست آوردن بینش های عمیق تر نسبت به مشکلاتی اعم از طیف کلی علم و فن آوری کمک کرده است، زیرا قوانین مقیاس بندی معمولاً منعکس کننده ویژگی های عمومی و اصول فیزیکی هستند که مستقل از پویایی مفصل و یا ویژگی های خاص از مدل های خاص می باشند. مکانیک سیالات و گذارهای فاز, نمونه های قابل توجهی هستند که در آن مقیاس بندی, اصول و یا ساختارهای مهم جهانی را روشن ساخته است، و پاسخ هایی را به مسائل عملی فراهم کرده است.

      این حدس معقول و منطقی به نظر می رسد که رفتار کلان سیستم های زنده ممکن است از قوانین قابل سنجشی پیروی نمایند که ویژگی های ضروری این سیستم ها را در بردارند، اگر اینها در واقع وجود داشته باشند. در تضاد با تنوع و پیچیدگی زیاد موجودات زنده، می توان سادگی رفتار مقیاس بندی فرآیندهای بیولوژیکی را یافت که در طیف گسترده ای از پدیده ها و طیف وسیعی از انرژی و جرم صادق است.

       همانطور که توسط مرجع [1] اشاره شده است, در زیست شناسی, مقیاس بندی مشاهده شده نوعاً یک قانون توان ساده است:  ، که در آن Y یک دامنه قابل مشاهده،   یک ثابت، و M جرم ارگانیسم است: نمای b معمولاً یک مضرب ساده از ¼ را تقریب می زند. در میان بسیاری از متغیرهای اساسی که از چنین قوانین مقیاس بندی پیروی می کنند, میزان سوخت و ساز، طول عمر، ضربان قلب، طول آئورت و ژنوم، ارتفاع درخت، جرم ماده خاکستری مغز، و دیگران قرار دارند [مرجع. [1] و منابع آن را ببینید[.

       میزان سوخت و ساز برای پستانداران و پرندگان با مقیاس  , چندین سال پیش به مدت حدود چهار مرتبه بزرگی در توده [1،2] نشان داده شده است. این کار توسط محققان پس از آن به سیستم های دیگر تعمیم داده شد و، با برخی از خصوصیات، نمای متابوبیک در سراسر تقریباً 27 مرتبه از دامنه در زندگی [1،3] یافت شده است. مثال های دیگر شامل ضربان قلب  ، و شعاعهای آئورت و تنه درخت   [1] می شوند.

       نقطه شروع درک منشا این مقیاس بندی, شناخت این مورد است که ساختارهای زنده بسیار پیچیده به یک انسجام تقریبی از تعداد زیادی از واحدهای میکروسکوپی موضع یافته نیاز دارند که باید در مد حدود، "دموکراتیک" و کارآمد [1] سرویس دهی شوند. برای مقابله با این چالش، گزینش طبیعی, شبکه های منشعب سازی فراکتال-مانند سلسله مراتبی را پیشرفت داده است که انرژی، کالا، و یا متابولیت ها، و اطلاعات را از مخازن ماکروسکوپی به سایت های میکروسکوپی توزیع می نمایند. مثالها عبارتند از سیستم های گردش خون حیوانات ، سیستم عروقی گیاهان، و شبکه های داخل سلولی.

        تلاش توانمند برای بهینه سازی حمل و نقل (ماده، انرژی، و اطلاعات) را می توان به عنوان ظهوری برای قوانین مقیاس بندی در سطح واقعی در نظر گرفت.

       می توان نشان داد که قوانین مقیاس بندی و رفتار دینامیکی کلان عام سیستم های بیولوژیکی, منعکس کننده محدودیت های ذاتی در خواص کلی چنین شبکه هایی است. با توجه به مرجع [1]، این محدودیت ها را می توان به شرح زیر در نظر گرفت:

• شبکه ها به تمام نواحی موضعی فعال از نظر بیولوژیک در هر دو سیستم های بیولوژیکی بالغ و در حال رشد خدمات رسانی می نمایند. چنین شبکه هایی (هیچ جایی بدون خدمات), پرکننده-فضا نامیده می شوند.

• واحدهای ترمینال شبکه، در داخل یک کلاس, نامتغیر هستند (واحدهای موضع یافته میکروسکوپی به طور متوسط  هیچ گونه تغییر قابل ملاحظه ای را نشان می دهند).

• موجودات زنده به سمت حالت مطلوب تکامل می یابند که در آن انرژی مورد نیاز برای توزیع منابع به حداقل می رسد (بهینه سازی شبکه).

Abstract

      The inter-relations and the complexity of modern urban spaces are difficult to analyse in a way that allows improving living conditions or help to ascertain optimal decisions for saving energy or improving sustainability. Carefully designed decisions and guidelines might produce unexpected results because of particularities, or complex sets of reactions from residents or economic counterparts. Complexity tends to increase with size, such as when, for instance, services tend to concentrate in large agglomerations, and transportation needs take on critical importance. Complex systems such as living organisms are known to follow approximate relationships as scaling laws between the variables that describe them. Some of these kinds of relationships are tested in relation to modern developed urban spaces, in which it is possible to find a reasonable continuity with the types of scales seen in living organisms, and some preliminary conclusions are drawn.

1. Introduction

      Large cities have a high degree of complexity and strong inter-relations among their inhabitants and surroundings. The degree of complexity and these inter-relations nowadays seem to produce favourable conditions, or better living conditions, as the size and number of large cities appear to increase. Urban planning in large cities is a formidable challenge, because of the range of previsions that must be taken into account. It would be very attractive if there were natural laws that guided growth, or at least yielded desirable conditions. However, detailed physical relationships between the variables that determine these conditions are very complex due to the complexity of the system and the multiple sets of variables needed to describe it, which are together considered as a physical system. Nevertheless, some ideas and tendencies seem to be shared by many modern cities: one should optimise such things as energy expenses, the transport of goods (including food, water, y), public and private transport, and pollution issues. It then seems reasonable to expect some general trends (if not ‘‘exact’’ laws) that modern cities should follow, and it should be acceptable to think about it as complex, physical systems.

      Then, we should learn from phenomenological relations in existing complex systems that have evolved over hundreds of millennia. As living organisms represent one of these systems, which have been largely studied,and are indeed a paradigm of complexity, studying general laws or general relationships in biology might give us an insight into our problem. In fact, it seems reasonable to conjecture that the coarse-grained behaviour of living systems might obey quantifiable universal laws that capture the systems’ essential features, as Ref. [1] does.

      Scaling, as a manifestation of the underlying general dynamics and geometry, is familiar throughout physics. It has helped scientists gain deeper insights into problems ranging across the entire spectrum of science and technology, as scaling laws typically reflect generic features and physical principles that are independent of the detailed dynamics or specific characteristics of particular models. Fluid mechanics and phase transitions are significant examples in which scaling has illuminated important universal principles or structures, and has provided responses to practical problems.

      It seems reasonable to conjecture that the coarse-grained behaviour of living systems might obey quantifiable laws that capture these systems’ essential features, if these do in fact exist. In contrast to the large diversity and complexity of living organisms, one finds the simplicity of the scaling behaviour of biological processes that holds true in a wide range of phenomena and a large range of energy and mass.

       As pointed out by Ref. [1], in biology the scaling observed is typically a simple power law: Y ¼ Y0Mb , where Y is some observable magnitude, Y0 a constant, and M the mass of the organism. The exponent b usually approximates a simple multiple of 1 4. Among the many fundamental variables that obey such scaling laws are metabolic rate, life span, heart rate, lengths of aortas and genomes, tree height, mass of cerebral grey matter, and others [see Ref. [1] and references therein].

       The metabolic rate for mammals and birds was shown to scale as M3/4 many years ago for about four orders of magnitude in mass [1,2]. This work was generalised by subsequent researchers to other systems, and, with some particularities, the metabolic exponent bE 3 4 is found across nearly 27 orders of magnitude in life [1,3]. Other examples include heart rate (bE 1 4), and the radii of aortas and tree trunks (bE 3 8) [1].

       The starting point to understanding the origin of this scaling is recognising that highly complex living structures require a close integration of massive numbers of localised microscopic units that must be serviced in an approximately ‘‘democratic’’ and efficient fashion [1]. To meet that challenge, natural selection has evolved hierarchical fractal-like branching networks that distribute energy, goods, or metabolites, and information from macroscopic reservoirs to microscopic sites. Examples include animal circulatory systems, plant vascular systems, and intracellular networks.

       The formidable quest for optimisation of transport (of matter, energy, and information) might be considered as giving rise to scaling laws in the actual level.

       It can be proposed that scaling laws and the generic coarse-grained dynamical behaviour of biological systems reflect the constraints inherent in the universal properties of such networks. According to Ref. [1], these constraints can be approached as follows:

Networks service all local biologically active regions in both mature and growing biological systems. Such networks are called space-filling (no place without service).

The networks’ terminal units are invariant within a class (microscopic localised units do not on average show any appreciable change).

Organisms evolve towards an optimal state in which the energy required for resource distribution is minimised (optimisation of the network).

چکیده

1. مقدمه

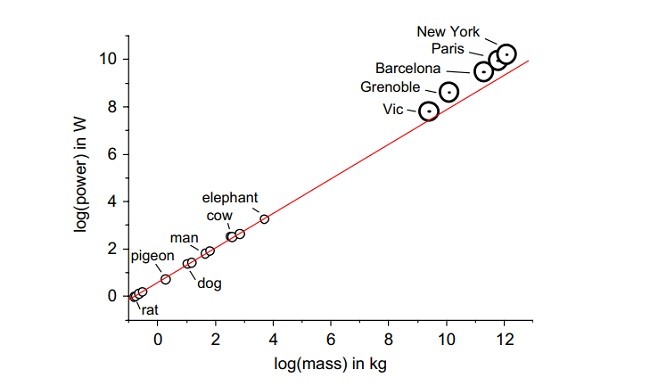
2. مقیاس بندی آلومتریک توان در شهرها

3. حمل و نقل ضربانی در شهرها

4. نتیجه گیری ها

Abstract

1. Introduction

2. Allometric scaling of power in cities

3. Pulsatory transport in cities

4. Conclusions

References