
دانلود رایگان مقاله ردیابی EEG ثابت با ریشه های مدل های ARMA
چکیده
ردیابی EEG ثابت با مدل های ARMA متغیر با زمان بحث شده است. یک روش برای تشخیص دوک ها در EEG موش ارائه شده است. این روش بر اساس ردیابی یک قطب سیستم واحد مدل ARMA است.
1 مقدمه
هدف تجزیه و تحلیل خودکار EEG, اغلب تشخیص اشکال موج خاص و یا تقسیم بندی EEG به دوره های شبه ثایت و طبقه بندی بعدی اینهاست. مشخص شده است که پارامترهای اتورگرسیو (خود کاهشی) (AR) و مدل های متوسط حرکت اتورگرسیو متوسط (ARMA), نمایشگر بازده تمایز معقول خوبی در بسیاری از موارد [1] هستند. با این حال، شرایطی وجود دارند که در آن کلاس های مختلف, مراتب مختلف مدل را ضروری می نمایند. برآورد مرتبه های مدل برای هر بخش از نظر محاسباتی غیرعملی خواهد بود و در عمل ما باید از مراتبی استفاده کنیم که برای هر کلاس کافی هستند. این به این معنی است که واریانس های تخمین های پارامتر برای کلاس هایی بزرگ خواهد بود که برای آن, مراتب بسیاری بالا هستند و بازده تمایز کاهش می یابد. با این حال، واریانس های ریشه های چند جمله ای مشخصه مدل, همه مثل این رفتار نمی کنند. برخی از ریشه ها می توانند واریانس های کم را حفظ کنند در حالی که افزایش در واریانس های پارامتر, بر دیگر ریشه ها, بیشتر از اینها اثر می گذارد.
استفاده از ریشه های مدل قبلاً برای طبقه بندی اعصار ثابت EEG پیشنهاد شده است [2]. همچنین مشاهده شده است که حملات صرعی را می توان با حرکت برخی از ریشه ها در صفحه مختلط پیش بینی نمود [3].
ما این نتایج را به EEG متغیر با زمان با استفاده از یک پیش بینی کننده تطبیقی برای تخمین پارامترهای مدل گسترش می دهیم که از آن ریشه های مربوط به بخش AR (قطب ها ) محاسبه می شوند. به عنوان مثال, ما از این روش برای بخش بندی و طبقه بندی الکتروکوتیکوگرام یک موش خوابالود استفاده می کنیم.
II. پیگیری پارامترها
مدل های متغیر با زمان (p,q) ARMA برای XT فرآیند را می توان به صورت زیر نوشت
xt = Xp k=1 ak(t)xt−k +Xq `=1 b`(t)et−` + et , (1)
که در آن et, فرآیند خطای پیش بینی است و پارامترهای با یک پیش بینی کننده تطبیقی برآورد می شوند. چندین الگوریتم وجود دارند که می توانند به عنوان پیش بینی کننده استفاده شوند. رایج ترین الگوریتم ها, فیلترهای LMS، RLS و Kalman هستند. ما در اینجا از الگوریتم حداقل مربعات بازگشتی (RLS) [4] استفاده می کنیم. برای بحث در مورد ردیابی EEG با فیلتر کالمن, [5] را مشاهده کنید.
که در آن θt = [ˆa1(t),..., aˆp(t), ˆb1(t),..., ˆbq(t)]0 (2) و ترانهاده توسط علامت پریم مشخص شده است. برای حفظ قابلیت ردیابی الگوریتم, ما باید داشته باشیم اما در غیر این صورت موازنه بین سرعت ردیابی و واریانس برآورد از طریق ضریب فراموشی کنترل می شود.
اگر برخی از روش های استاندارد، مانند محاسبه مقادیر ویژه ماتریس همدم مرتبط استفاده شود, محاسبه تمام ریشه ها از برای هر زمان را می تواند محاسباتی بیش از حد گران باشد.
با این حال، تقریب توسط ردیابی یک ریشه یا چند ریشه بر اساس تخمین های قبلی را می توان با روش های مختلف انجام داد [6]، [7]. ما یک ریشه واحد از چند جمله ای را با یک تکرار روش نیوتن در یک زمان ردیابی می نماییم.
III. تشخیص دوک های EEG موش
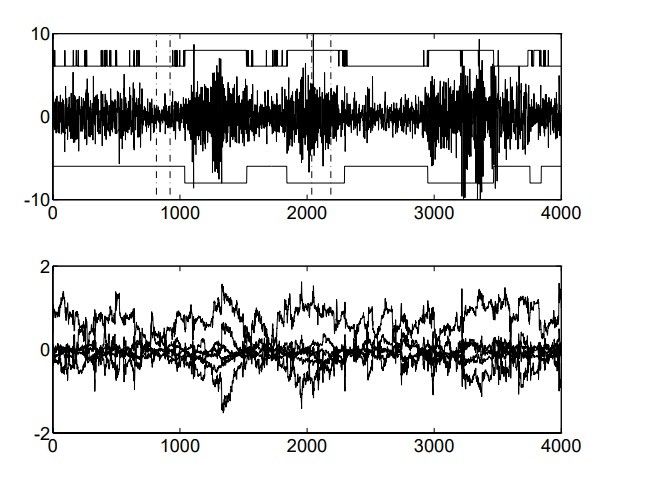
دوک های EEG موش, اشکال موج شبیه-انفجار هستند هنگامی که موش ها چرت زن هستند. فرکانس رخداد آنها به عنوان مثال، مرتبط با قابلیت یادگیری و اثر داروهای خاص است. یک دوره نوعی از شکل موج موش EEG در شکل 1 ارائه شده است. ویژگی های طیفی دوک ها از ویژگی های طیفی پس زمینه قابل تشخیص هستند و در نتیجه استفاده از مدل های پارامتری در مثال تشخیص مشهود است [8]. EEG موش را می تواند به عنوان ضامن بین حالات دوک و غیر دوک توصیف نمود. هر دو حالت را می توان با ARMA (2 4) مدلسازی نمود.
IV. روش
روش تشخیص دوک به شرح زیر بود:
1. دو بخش از داده ها، یکی برای هر کلاس را انتخاب کنید. از این مجموعه های یادگیری به عنوان کلاس ها استفاده نمایید.
2. این بخش ها را از طریق RLS برای به دست آوردن برآوردهای پارامتر برای مراقبت کلاس ها به منظور تنظیم مقادیر اولیه اجرا نمایید.
3. ریشه های مورد نظر را محاسبه نمایید و مرز طبقه بندی (تشخیص) را تعیین نمایید.
4. داده های کلی را از طریق RLS و یک ردگیر ریشه را اجرا نمایید، بیشتر از طریق یک پس پرداز اختیاری (به عنوان مثال فیلتر میانه) طبقه بندی و اجرا نمایید.
Abstract
The tracking of nonstationary EEG with time-varying ARMA models is discussed. A method for detecting spindles in rat EEG is presented. The method is based on tracking of a single system pole of the ARMA model.
I. Introduction
The end to automatic analysis of EEG is often detection of certain waveforms or segmentation of the EEG into pseudostationary epochs and the subsequent classification of these. The parameters of autoregressive (AR) and autoregressive moving average (ARMA) models have been found to exhibit reasonably good discrimination efficiency in many cases [1]. However, there are situations where different classes would necessitate different orders of the model. The estimation of model orders for each segment would be computationally unfeasible and in practice we have to use orders that are sufficient for each class. This means that the variances of the parameter estimates will be large for the classes for which the orders are too high and the discrimination efficiency decreases. However, the variances of the roots of the model characteristic polynomials do not all behave like this. Some roots can retain small variances while the increase in the parameter variances affects other roots more than these.
The use of model roots has been proposed earlier for the classification of stationary epochs of EEG [2]. It has also been observed that epileptic seizures can be predicted by the movement of some roots in the complex plane [3].
We extend these results to time-varying EEG by using an adaptive predictor to estimate the model parameters from which the roots corresponding to the AR part (poles) are calculated. As an example we use this method to segment and classify the electrocorticogram of a drowsy rat.
II. Tracking of parameters
Time-varying ARMA(p,q) models for the process xt can be written as
xt = Xp k=1 ak(t)xt−k +Xq `=1 b`(t)et−` + et , (1)
where et is the prediction error process and the parameters ak(t) and b`(t) are estimated with an adaptive predictor. There are several algorithms that can be used as predictors. The most common ones are the LMS, RLS and the Kalman filters. We use here the recursive least squares (RLS) algorithm [4]. See [5] for discussion on the tracking of EEG with the Kalman filter.
where θt = [ˆa1(t),..., aˆp(t), ˆb1(t),..., ˆbq(t)]0 (2) and the transpose is denoted by prime. To maintain the tracking capability of the algorithm we must have λ < 1 but otherwise the trade-off between tracking speed and estimate variance is controlled via the forgetting factor λ.
The calculation of all the roots from ˆak(t) for each time can be computationally too expensive if some standard method, such as the calculation of the eigenvalues of the associated companion matrix, is used.
However, the approximation by tracking of a root or several roots based on previous estimates can be performed with various methods [6],[7]. We track a single root of the polynomial with one iteration of the Newton’s method at a time.
III. Detection of Rat EEG Spindles
Rat EEG spindles are burst-like waveforms occurring when rats are drowsy. Their frequency of occurrence correlates e.g. with the learning capability and the effect of certain drugs. A typical epoch of rat EEG waveform is presented in Fig. 1. The spectral characteristics of spindles are distinguishable from that of background and therefore the use of parametric models in e.g. spindle detection is evident [8]. The rat EEG can be described as toggling between the spindle and non-spindle states. Both states can be modeled with ARMA(4, 2) models.
IV. The Method
The procedure of the spindle detection was as follows:
1. Select two segments from the data, one for each class. Use these as the learning sets for the classes.
2. Run these segments through RLS to obtain parameter estimates for the classes taking care to adjust the initial values.
3. Calculate the roots of interest and determine the classification (detection) boundary.
4. Run the whole data through RLS and a root tracker, classify and run further through an optional postprocessor (e.g. a median filter).
چکیده
1 مقدمه
II. پیگیری پارامترها
III. تشخیص دوک های EEG موش
IV. روش
V. نتایج
VI. نتیجه گیری ها
Abstract
I. Introduction
II. Tracking of parameters
III. Detection of Rat EEG Spindles
IV. The Method
V. Results
VI. Conclusions
References
