دانلود رایگان مقاله حداکثر سازی تاثیر مقیاس بندی با تجرید شبکه

چکیده

          تحت محدودیت بودجه‌ی تبلیغاتی، بیشینه‌سازی انتخاب محصول در یک شبکه‌ی اجتماعی مشتری، یک مورد خاص و مهم از مساله‌ی عمومیِ بیشنه‌سازی تاثیر می‌باشد. تکنیک‌های بهینه‌سازیِ خاصی که همبستگی‌ها و تاثیرات جامعه‌‌ی محلی را در نظر می‌گیرند، می‌توانند عملکرد بهتری نسبت تکنیک‌های شبکه‌بنیان داشته باشند که باعث تعاملاتی می‌شوند که منبعث از بازاریابیِ محصولات متعدد برای یک گروه مشتری می‌باشد. با اینحال، این انجامپذیر است که از روشهای بهینه‌سازیِ دقیقی استفاده کنیم که از عملیات ماتریس پرهزینه‌ روی شبکه‌های بزرگ، بدون تکنیک‌های محاسباتیِ موازی استفاده ‌کند. در این فصل، یک رویکرد بیشینه‌سازی تاثیرِ سلسله‌مراتبی را برای بازاریابی محصول ارائه می‌دهیم که یک سلسله‌مراتب تجرید را برای مقیاس‌بندی تکنیک‌های بهینه‌سازی برای شبکه‌های بزرگ، می‌سازد. یک راه‌حل دقیق روی پارتیشن‌های کوچکترِ شبکه اِعمال می‎‌شود و مجموعه‌ای کاندید از گره‌های تاثیرگذار، به سمت بالا و به بازنمود مجردِ شبکه‌ی اریجنال منتشر می‌شود که اطلاعات مسافت را حفظ می‌کند. این فرایند تجرید، راه‌حل و انتشار، تا زمانی تکرار می‌شود که شبکه‌ی مجردِ حاصله، آنقدر کوچک شود که بتواند دقیقاً حل گردد.

1. مقدمه

          در بازار امروز، تبلیغ صرفاً موضوعی که مشتریان را به خرید محصول متقاعد کند نیست، بلکه متقاعد کردن شبکه‌ی اجتماعی آنها به انتخاب یک سبک زندگی، مدنظر است. اکنون کاملاَ مشخص شده است که پیوندهای اجتماعی بین کاربران نقش مهمی در شکل‌دهی به رفتار آنها ایفا می‌کند. یکی از راه‌های تحقق این امر، از طریق تاثیر اجتماعی است که طیِ آن، یک رفتار یا ایده می‌تواند بین دوستان فراگیر شود. با مدنظر قرار دادن فاکتور‌هایی نظیر نوع‌دوستی و متغیرهای مداخله‌گرِ مشاهده‌نشده، می‌توان به بررسی دقیق و آماریِ همبستگی این رفتارها در شبکه‌ی اجتماعی پرداخت. هدف از راهبردهای بازاریابی ویروسی، ارتقای همبستگی این رفتارها جهت خلق زنجیره‌ای از اطلاعات است که تعداد زیادی از مشتریان در آن، از مجموعه‌ای بسیار کوچکتر از افرادِ آگاه تقلید می‌کنند، که قبل از سایرین توسط طرح‌های بازاریابی اقناع شده‌اند.

          بازاریابی با بودجه‌ی محدود را می‌توان نسخه‌ای تخصصی از مساله‌ی بیشینه‌سازیِ تاثیر تلقی کرد که هدف از آن، تبلیغ گره‌های دانه‌ای جهت اصلاح دیدگاه‌های درون شبکه –بر مبنای مدل انتشار تاثیر- می‌باشد. مدلهای انتشار پرکاربرد نظیر مدل آستانه‌ی خطی (LTM) و مدل مستقل آبشاری (ICM) فرض را بر این می‌گذارند که احتمال پذیرش یک گره، مشروط به دیدگاه‌های همسایگیِ شبکه‌ی محلی می‌باشد. قسمت اعظم وظیفه‌ی پیشینِ بیشینه‌سازی تاثیر، از این دو مدل تفاکتور استفاده می‌کند. از زمان مدل LT و مدل ICیِ اریجنال، سایر مدلهای تعمیم‌یافته، برای حیطه‌های مختلف و مصارف تخصصی مطرح شده‌اند. مثلاً مدل آبشاری کاهنده، مدلهایی را که در جامعه‌شناسی و انجمن‌های اقتصادی بکار می‌رود را تعمیم می‌دهد، چراکه در این جوامع، یک رفتار بصورت آبشاری و بر مبنای یک قاعده‌ی احتمالاتی پراکنده می‌شود و با مجموعه‌ای از گره‌هایی که آن رفتار را می‌پذیرند، شروع می‌شود. در مقابلِ مدل ارجینال IC، در مدل آبشاری کاهنده، احتمال انتشار تاثیر از یک گره فعال، ثابت نیست. همینطور، نسخه‌های تعمیم‌یافته‌ی مدل آستانه‌ی خطی نیز معرفی شده‌اند. سادگیِ این مدلهای انتشار، تحلیل نظری را تسهیل می‌کند اما مدلی واقع‌گرایانه از ملاحظات بازاریابی به دست می‌دهد: نظیر تفاکتور بین تبلیغاتِ محصولات متعدد و اثرات عضویت در جامعه بر انتخاب محصول.

           جهت پرداختن به این مسائل، در کار قبلی (رفرنس 21)، مدلی از انتخاب محصول در شبکه‌های اجتماعی را مطرح کردیم که این فاکتور‌ها را در نظر می‌گیرد و از یک فرمولاسیون بهینه‌سازی جهت محاسبه‌ی بهترین راهبرد بازاریابی –با فرض بودجه‌ی محدود- استفاده می‌کند. این فاکتور‌های اجتماعی می‌توانند از متغیرهای مستقل مختلفی استفاده کنند: نظیرِ پیوندهای بین دوستان و همسایگان، جایگاه اجتماعی و وضعیت اقتصادیِ عامل‌ها . مشخصات مشابهی نیز بر مردم در سایر حیطه‌ها تاثیر می‌گذارند؛ مثلاً، آرال و والکر  تاثیر جایگاه اجتماعی را بر فاکتورِ «تاثیر»ِ مردم در فیسبوک اثبات کرده‌اند. باورمان بر این است که در بازاریابی، تمام این فاکتورها بر احتمال تاثیرپذیری مشتریان و تانایی آنها در تاثیرگذاری بر سایرین، موثرند.

           برخورداری از یک مدل واقع‌گراتر، جهت غلبه بر اثرات تبلیغات منفی مفید واقع می‌شود؛ این تبلیغات منفی که از جانب شرکتهای رقیب به سوی مصرف‌کننده‌ها سرازیر می‎شوند، قصد دارند مصرف‌کننده را به خرید کالاهای خود ترغیب و از خرید کالاهای سایر شرکتها منصرف سازند. ضروری است که انتشار تاثیر منفی را نیز مدلسازی کنیم، چراکه انتشار می‌یابد و می‌تواند تاثیری قوی‌تر و مُسری‌تر از تاثیر مثبت، بر تصمیم‌گیری‌های افراد داشته باشد.

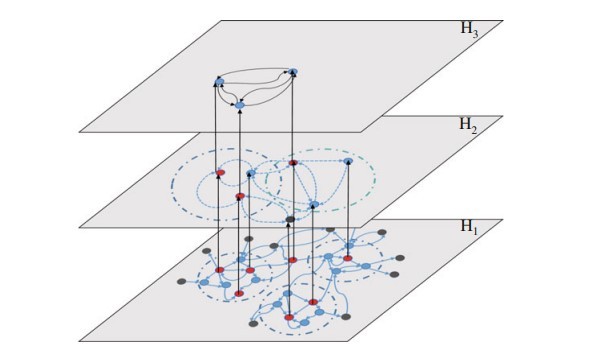
            محدودیت اصلیِ این نوع رویکرد و رویکردهای مشابه، این است که شامل معکوس ماتریس می‌شود که اندکی کمتر O(N3) است و یک فاکتور محدودساز است که مانع تبدیل این الگوریتم‌ها به شبکه‌های بزرگتر می‌شود. در این فصل، یک رویکرد بیشینه‌سازیِ تاثیر سلسله‌مراتبی را مطرح می‌کنیم که طرفدارِ «تقسیم و غلبه» است –یعنی شبکه به چند شبکه‌ی کوچکتر تقسیم می‌شود که می‌توان آنها دقیقاً با تکنیک‌های بهینه‌سازی و با در نظر گرفتن یک مدل ICی تعمیم‌یافته جهت تعیین مجموعه‌ای از گره‌های دانه، حل نمود. از گره‌های کاندید جهت خلق یک نسخه‌ی خلاصه‌ی حافظِ مسافت از شبکه، استفاده می‌شود که مدل تاثیر متراکم را بین پارتیشن‌ها حفظ می‌کند. در اینجا نشان می‌دهیم که این تکنیک خلاصه‌سازی را چطور می‌تواند الگوریتم‌های بیشینه‌سازیِ تاثیر را جهت سناریوهای بزرگترِ انتخاب محصول، مقیاس‌بندی کند. بعلاوه قضیه‌ای را مطرح می‌سازیم که نشان می‌دهد مدل سیستم‌های اجتماعیِ واقع‌گرا، دارای نقطه‌ای ثابت است، که راهبردِ بهینه‌سازیِ انتخاب محصول را معتبر می‌سازد.

        این فصل به ترتیب زیر سازماندهی شده است. بخش 2 مروری بر کارهای پژوهشی دارد که در زمینه‌ی بیشینه‌سازیِ تاثیر انجام گرفته‌اند. بخش 3 روش مطروحه‌ی ما، بیشینه‌سازیِ تاثیر سلسله‌مراتبی (HIM) را معرفی می‌کند، و عملیات مدل واقع‌گرای انتخاب محصول را که در رفرنس 21 ارائه شده است، خلاصه می‌کند. در بخش 4، ما روش خودمان را در مقابل سایر رویکردهای بیشینه‌سازیِ تاثیر، هم در شبکه‌های واقعی و هم ساختگی، ارزیابی می‌کنیم. این فصل، ضمیمه‌ای بر کار قبلی ما (رفرنس 22) است که تکنیک‌های پیش‌پردازش را برای شبکه‌های بزرگ معرفی می‌کند و ارزیابی جامع‌تری از چارچوب ما، در خصوص سه دیتابِیس دنیای واقعیِ بزرگتر ارائه می‌دهد. این فصل را با مبحثی در خصوص پژوهش‌های آتی به پایان می‌بریم.

2. پژوهش‌های مرتبط

         بیشینه‌سازیِ تاثیر را می‌توان اینگونه توصیف کرد: تعیین مجموعه‌ای کوچک از گره‌ها که قادر به راه‌اندازی آبشارهای بزرگی از رفتار هستند که در تمام شبکه پخش می‌شود. این مجموعه از گره‌ها را می‌توان با استفاده از رویکردهای احتمالاتی (مثلاً رفرنس‌های 2و 17) یا تکنیک‌های مبتنی بر بهینه‌سازی کشف نمود. رفرنس‌های 12 و 21، با بهینه‌سازی تاثیر، بصورت یک مساله‌ی بهینه‌سازی محدب رفتار می‌کنند؛ این مساله برای تاثیرگذاری بر جوامع کوچک انجامپذیر است اما برای مسائل بزرگتر خیر/ به دلیل ضوابط محاسباتیِ ماتریس، این رویکردها زمانی ناکام می‌مانند که تعداد عامل‌های سیستم افزایش یابند. الگوریتم HIM با استفاده از یک رویکرد سلسله‌مراتبی جهت تبدیل سیستم به ماتریس‌های کوچکتر، بر این ناکارآمدی غلبه می‌کند.

       مدل اچ آی ام (HIM =بیشینه‌سازیِ تاثیر سلسله‌مراتبی) جهت کار روی سیستم اجتماعیِ پیچیده‌ای طراحی شده‌ است که در آن، فاکتورهای چندگانه بر انتشارِ تاثیر، اثر می‌گذارند. حالتی ساده‌تر نیز توسط گروه‌های پژوهشیِ متعدد مورد بررسی قرار گرفته‌ است که هدف از آن بهبود پژوهش‌های اولیه‌ی کِمپ  روی رویکردهای حریصانه جهت بیشینه‌سازیِ تاثیر می‌باشد. مثالهایی از تسریع احتمالی، شامل نوآوری‌هایی نظیر استفاده از یک مدل آبشاریِ تاثیر مبتنی بر کوتاه‌ترین مسیر یا یک الگوریتم بهینه‌سازیِ lazy-forward می‌باشند که جهت کاهش تعداد ارزیابی‌های صورت‌گرفته روی گستره‌ی تاثیر گره‌ها می‌باشند. روش‌‌های اکتشافیِ هوشمند با موفقیت بکار رفته‌اند تا سرعت محاسبات را هم در مدل LT و هم در مدل IC بالا ببرند. در این فصل، به جای استفاده از مدلهای آبشاریِ اریجنال که توسط کِمپ و همکارانش تهیه شد، یک مدل آبشاری معرفی می‌کنیم که تعاملات محصول و تفاوتهای جامعه را در انتشار تاثیر، مدنظر قرار می‌دهد.

Abstract

        Maximizing product adoption within a customer social network under a constrained advertising budget is an important special case of the general influence maximization problem. Specialized optimization techniques that account for product correlations and community effects can outperform network-based techniques that do not model interactions that arise from marketing multiple products to the same consumer base. However, it can be infeasible to use exact optimization methods that utilize expensive matrix operations on larger networks without parallel computation techniques. In this chapter, we present a hierarchical influence maximization approach for product marketing that constructs an abstraction hierarchy for scaling optimization techniques to larger networks. An exact solution is computed on smaller partitions of the network, and a candidate set of influential nodes is propagated upward to an abstract representation of the original network that maintains distance information. This process of abstraction, solution, and propagation is repeated until the resulting abstract network is small enough to be solved exactly.

1 Introduction

          Advertising in today’s market is no longer viewed as a matter of simply convincing a potential customer to buy the product but of convincing their social network to adopt a lifestyle choice. It is well known that social ties between users play an important role in dictating their behavior. One of the ways this can occur is through social influence where a behavior or idea can propagate between friends. By considering factors such as homophily and possible unobserved confounding variables, it is possible to examine these behavior correlations in a social network statistically [1]. The aim of viral marketing strategies is to leverage these behavior correlations to create information cascades in which a large number of customers imitate a much smaller set of informed people, who are initially convinced by targeting marketing schemes.

          Marketing with a limited budget can be viewed as a specialized version of the influence maximization problem in which the aim is to advertise to the optimal set of seed nodes to modify opinion in the network, based on a known influence propagation model. Commonly used propagation models such as Linear Threshold Model (LTM) and Independent Cascade Model (ICM) assume that a node’s adoption probability is conditioned on the opinions of the local network neighborhood [15]. Much of the previous influence maximization work [8, 10, 25] uses these two interaction models. Since the original LT model and IC model, other generalized models have been proposed for different domains and specialized applications. For instance, the decreasing cascade model generalizes models used in the sociology and economics communities where a behavior spreads in a cascading function according to a probabilistic rule, beginning with a set of nodes that adopt the behavior [15]. In contrast with the original IC model, in the decreasing cascade model the probability of influence propagation from an active node is not constant. Similarly, generalized versions of the linear threshold model have been introduced (e.g., [5, 23]). The simplicity of these propagation models facilitates theoretical analysis but does not realistically model specific marketing considerations such as the interactions between advertisements of multiple products and the effects of community membership on product adoption.

         To address these problems, in previous work [21], we developed a model of product adoption in social networks that accounts for these factors, along with a convex optimization formulation for calculating the best marketing strategy assuming a limited budget. These social factors can emerge from different independent variables such as ties between friends and neighbors, social status, and the economic circumstance of the agents. Similar properties have been shown to influence people in other domains; for instance, Aral and Walker demonstrated the effect of social status on the influence factor of people on Facebook [3]. We believe that in marketing, all these factors affect the customers’ susceptibility to influence and their ability to influence others.

         Having a more realistic model is particularly useful for overcoming negative advertisement effects in which the customers refrain from purchasing any products after being bombarded with mildly derogatory advertisement from multiple advertisers trying to push their own products. It is critical to model the propagation of negative influence as well since it propagates and can be stronger and more contagious than positive influence in affecting people’s decisions [7].

        The main limitation of this and similar types of optimization approaches is that they involve matrix inversion which is slightly less than O(N3) and is the limiting factor preventing these algorithms from scaling to larger networks. In this chapter, we propose a hierarchical influence maximization approach that advocates “divide and conquer”—the network is partitioned into multiple smaller networks that can be solved exactly with optimization techniques, assuming a generalized IC model, to identify a candidate set of seed nodes. The candidate nodes are used to create a distance-preserving abstract version of the network that maintains an aggregate influence model between partitions. Here we demonstrate how this abstraction technique can be used to scale influence maximization algorithms to larger product adoption scenarios. Moreover, we present a theorem which shows that the realistic social system model has a fixed-point, validating the strategy of optimizing product adoption at the steady state.

        The chapter is organized as follows. Section 2 provides an overview of the related work in influence maximization. Section 3 introduces our proposed method, Hierarchical Influence Maximization (HIM) [22], as well as summarizing the operation of the realistic product adoption model introduced by [21]. We evaluate our method versus other influence maximization approaches on both real and synthetic networks in Sect. 4. This chapter extends on our earlier work [22] by introducing new preprocessing techniques for large networks and presenting a more comprehensive evaluation of our framework on three larger real-world datasets. We end the chapter with a discussion of future work.

2 Related Work

         Influence maximization can be described as the problem of identifying a small set of nodes capable of triggering large behavior cascades that spread through the network. This set of nodes can be discovered using probabilistic approaches (e.g., [2, 17]) or optimization-based techniques. [12, 21] treat influence maximization as a convex optimization problem; this is feasible for influencing small communities but does not scale to larger scale problems. Due to the matrix computation requirements, these approaches fail when the number of agents in the system increases. Our HIM algorithm overcomes this deficiency by using a hierarchical approach to factor the system into smaller matrices.

        The HIM model is designed to work on a complex social system where multiple factors affect the propagation of influence. The simpler case, where the network topology alone dictates activation spread, has been examined by multiple research groups, seeking to improve on Kempe’s early work on greedy approaches for influence maximization [14]. Examples of possible speedups include innovations such as the use of a shortest-path based influence cascade model [16] or a lazy-forward optimization algorithm [19] to reduce the number of evaluations on the influence spread of nodes. Clever heuristics have been used very successfully to speed computation in both the LT model (e.g., the PMIA algorithm [8]) and also the IC model [25]. In this chapter, instead of using the original cascade models by Kempe et al. we introduce a cascade model that accounts for product interactions and community differences in influence propagation.

چکیده

1. مقدمه

2. پژوهش‌های مرتبط

3. روش

3.1 مدل بازار

3.2 مدل مستقل آبشاریِ تعمیم‌یافته

3.3 الگوریتم HIM

3.3.1 تاثیر دنیای بیرون

3.3.2 انتخاب گره

3.3.3 همگرایی

3.3.4 سلسله‌مراتب آپدیت

3.3.5 معیارهای پایان‌بخشی

3.3.6 رویه‌ و روالِ بهینه‌سازی

4. ارزیابی

4.1 ستاپِ آزمایشی

4.2 معیارها

4.3 دیتاسِت ساختگی

4.3.1 اثربخشی بازاریابی

4.3.2 زمان اجرا

4.3.3 تشابهِ ژاکارد

4.4 دیتاسِت (مجموعه‌ی داده‌ها) دنیای واقعی

4.4.1 اثربخشیِ بازاریابی

4.4.2 تحلیل توزیع‌های درجه‌ی دیتاسِت

4.4.3 بهینه‌سازی با روش اکتشافیِ درجه‌بنیان

5. نتیجه و کارهای آتی

منابع

Abstract

1 Introduction

2 Related Work

3 Method

3.1 Market Model

3.2 Generalized ICM

3.3 HIM Algorithm

3.3.1 Outside World Effect

3.3.2 Node Selection

3.3.3 Convergence

3.3.4 Update Hierarchy

3.3.5 Termination Criteria

3.3.6 Optimization Procedure

4 Evaluation

4.1 Experimental Setup

4.2 Benchmarks

4.3 Synthetic Dataset

4.3.1 Marketing Effectiveness

4.3.2 Run-Time

4.3.3 Jaccard Similarity

4.4 Real-World Datasets

4.4.1 Marketing Effectiveness

4.4.2 Analysis of Dataset Degree Distributions

4.4.3 Optimization with Degree-Based Heuristic

5 Conclusion and Future Work

References