دانلود رایگان مقاله الگوریتم ژنتیک چندگانه برای حل مساله زمان بندی در محیط کارگاهی

خلاصه

         این مقاله به حل مساله زمان‌بندی کارگاهی در یک دنیای واقعی می پردازد و الگوریتم جدیدی را به عنوان راه حل ارائه می‌دهد. ابتدا مشخصات اختصاصی کار هم‌زمان و شبانه را در فرآیند تولید ترانسفورماتور، مورد بررسی قرار می‌دهیم. برای حل مساله در یک زمان منطقی و قابل قبول،الگوریتم ژنتیک را پیشنهاد می‌شود. این الگوریتم، با هدف به حداقل رساندن تاخیر کل، روش الگوریتم اکتشافی Nawaz-Enscore-Ham (NEH)، که یک الگوریتم جستجوی محلی (بهینه سازی) است را با قانون تخصیص دستگاه، تلفیق می‌کند. نتایج آزمایشگاهی نشان می‌دهد که، این الگوریتم پیشنهادی از الگوریتم NEH "که یک الگوریتم ژنتیک ساده است" و پنج قانون توزیع امکانات بر حسب عملکرد تاخیر کلی متوسط و شاخص انحراف نسبی، بهتر عمل می‌کند. الگوریتم پیشنهادی برحسب راندمان و توانایی که دارد رقابتی‌تر جلوه می‌کند.

1. معرفی

         حل مساله زمان‌بندی در محیط کارگاهی در بسیاری از سیستم‌های تولید معمول است. در محیط های خاصی، دستگاه‌های موازی از کپی های متعددی تشکیل شده و در پایگاه‌های متعدی دسته بندی می‌شوند. برای این محیط‌های تولید، مدل حل مساله زمان‌بندی در محیط کارگاهی به روش قدیمی نامناسب است،زیرا برخی پایگاه ها از دستگاه‌های موازی استفاده می‌کند. این نوع مسائل می توانند تحت روش حل مساله زمان‌بندی کارگاهی چندگانه (HFSP) تعریف شوند. 

         حل مساله محیط کارگاهی چندگانه تعمیم و توسعه ای از سیستم تولید در محیط کارگاهی قدیمی است. این سیستم شامل دو یا چند جایگاه به طور ترتیبی و و یک یا چند دستگاه موازی در هر جایگاه است. مثال های حل مساله محیط کارگاهی چندگانه شامل تولید کفپوش، صنعت بطری شیشه ای و غیره هستند (Lopez & Roubellat 2008). 

         در این نوع کارگاه ها مشکل اصلی، تخصیص وظیفه به دستگاه‌ها در هر جایگاه  و توالی مشاغل اختصاص داده شده به دستگاه‌ها است. (HFSP) ها به طور گسترده ای مورد مطالعه و بررسی قرار گرفته اند، اگر چه اغلب موارد از نوع ان پی سخت  می‌باشند (Linn & Zhanh,1999)..

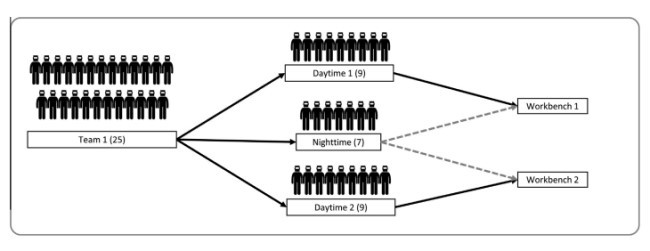
         این مقاله روی مساله زمان‌بندی در محیط کارگاهی چندگانه با دو دو محدودیت اختصاصی متمرکز شده است، در نظر گرفتن تیم کاری شبانه و روزانه، کار هم‌زمان انواع ترتیب های خاص. انگیزه تحقیق ما سیستم تولید ترانسفورماتور و تعداد شرایط قابلیت استفاده در بین انواع مختلف تولیدات و دستگاه‌هاست. در این مورد، راه حل ممکنی که تاخیر کلی را به حداقل می‌رساند ( یعنی زمان کلی که با آن ترتیب پردازش به تاخیر می‌افتد) به طرز حیاتی مهم است، زیرا هزینه خسارت مشاغل دارای دیرکرد اثر تعیین کننده ای روی شرکت دارد. 

         علاوه بر خصوصیات  (HFSP) عمومی، محدویت‌هایی به لحاظ وجود زمان انتظار بین مراحل متوالی یک کار  و لحاظ کردن کار شبانه یا کار هم‌زمان در هر مرحله، وجود دارد. 

        این مقاله به شکل زیر سازمان‌دهی شده است. در بخش آینده، تحقیقات قبلی در حل مساله زمان‌بندی کارگاهی چندگانه، مورد بررسی قرار می‌گیرد. این مساله و محدودیت های سیستم تولید ترانسفورماتور در بخش 3 تعریف می‌شود. سپس الگوریتم ژنتیک چندگانه برای حل این مساله در بخش 4 ارائه می شود. در بخش 5 نتایج بدست آمده برای تصدیق شیوه عملکرد انجام شده، خلاصه می‌شود. نهایتا، نتایج و زمینه‌های مطلوب برای تحقیقات مطرح می‌شوند.

2. بررسی نوشته های وابسته به حرفه علمی

         Arthanary  و Ramamurthy (1971) روش (HFSP) حل مساله زمان‌بندی در محیط چندگانه را مطرح نموده و الگوریتم شاخه و حد را ارائه کردند.Kochar  و  Morris در سال (1987) الگوریتم ابتکاری  (اکتشافی) برای به حداقل رساندن میانگین زمان جریان را برای مساله خط جریان تغییرپذیر با بافرهای محدود، توسعه دادند.آنها مساله را به دو زیر مساله تقسیم کردند، توالی نقطه ورود و دیسپاچینگ . HFSP دو مرحله ای برای NP-hard  به‌ ‌وسیله Gupta (1988) مطرح شده است. بعدا (Gupta,Harriri & Potts) در سال 1997 نشان دادند که HFSP دو مرحله ای غیرپیشگرانه به ظن قوی NP-hard است. 

        روش دقیق مبتنی بر مدل کردن ریاضی برای یافتن راه حل بهینه HFSP، می‌تواند عملکرد قوی‌تری را نسبت به روش ابتکاری تضمین نماید. Fattahi, Hosseini, Jolai, and Tavakkoli-Moghaddam  (2014) الگوریتم حد وشاخه را توسعه دادند که زمان تنظیم و تجمیع عملکردها را برای به حداقل رساندن زمان اتمام آخرین کار (Makespan)  در نظر می‌گرفت. (Sun و Yu) در سال 2015  HFSP دومرحله ای با محدودیت دسته‌ای و زمان پردازش متغیر از طریق روش آزاد سازی لاگرانژین را بررسی کردند. در واقع،  به خاطر ماهیت NP-hard بودن آنها، روش‌های دقیق تنها به مسائلی با اندازه کوچک قابل اعمال هستند. بنابراین، روش‌های ابتکاری برای بدست آوردن تقریب‌های مطلوب در زمان قابل قبول به کار گرفته می‌شوند(Ribas,Leisten & Framinan 2010 ). مثال‌هایی از الگوریتم ابتکاری  عبارتند از جستجوی همسایگی، شبیه سازی تبریدی و الگوریتم ژنتیک.

Abstract

        This paper addresses a hybrid flow shop scheduling problem with real-world constraints, and proposes a novel algorithm for its solution. We first discuss the distinguishing characteristics of nighttime and simultaneous work in the transformer manufacturing process. To solve the problem within a reasonable time, we propose a hybrid genetic algorithm. This algorithm combines the Nawaz–Enscore–Ham (NEH) heuristic, a local search algorithm, and a machine allocation rule with the aim of minimizing the total tardiness. Our experimental results show that the proposed algorithm outperforms the NEH algorithm, a simple genetic algorithm, and five existing dispatching rules in terms of average total tardiness performance and relative deviation index. The proposed algorithm is also shown to be competitive with respect to its efficiency and robustness.

1. Introduction

       The flow shop scheduling problem is common in many production systems. In certain environments, parallel machines are made up of multiple copies and grouped into stages. For these production environments, the traditional flow shop scheduling model is inappropriate, because some stages utilize parallel machines. This type of problem can be defined as a hybrid flow shop scheduling problem (HFSP).

         The hybrid flow shop is an extension of the production system in a traditional flow shop. It consists of two or more stages in series and one or more parallel machines at each stage to increase productivity and flexibility. Examples of hybrid flow shop problems are floor covering production, glass-bottle industry, and so on (Lopez & Roubellat, 2008).

        In this type of shop, the major issues are the allocation of jobs to machines at each stage, and the sequence of jobs assigned to each machine. HFSPs have been extensively studied; however, most examples are NP-hard (Linn & Zhang, 1999).

       This paper focuses on the scheduling problem in hybrid flow shops with two distinguishing constraints: the consideration of daytime and nighttime work teams and simultaneous work of specific order types. Our research is motivated by an industrial transformer manufacturing system with a number of availability conditions between various product types and machines. In this case, a feasible solution that minimizes the total tardiness (that is, the total time by which order processing is delayed) is vitally important, because the penalty cost of tardy jobs has a detrimental effect on a company.

        In addition to the characteristics of the general HFSP, there are constraints on the waiting times between successive stages of a job, as well the consideration of nighttime work and simultaneous work at each stage.

       This paper is organized as follows. In the next section, previous research into hybrid flow shop scheduling is reviewed. The problem and constraints of a transformer manufacturing system are defined in Section 3, and a hybrid genetic algorithm to solve this problem is then proposed in Section 4. Section 5 summarizes the results of experiments to verify our approach. Finally, our conclusions and areas for further research are discussed in Section 6.

2. Literature review

        Arthanari and Ramamurthy (1971) considered the HFSP, and proposed the first Branch and Bound method. Kochhar and Morris (1987) developed heuristic algorithms to minimize the mean flow time for the flexible flow line problem with finite buffers. They divided the problem into two sub problems: entry point sequencing and dispatching. The two-stage HFSP was shown to be NP-hard by Gupta (1988). Gupta, Hariri, and Potts (1997) then showed that a non-preemptive two-stage HFSP is NP-hard in the strong sense.

       Exact approaches based on mathematical modeling can ensure higher performance than heuristic methods in finding optimal solutions of HFSP. Fattahi, Hosseini, Jolai, and Tavakkoli-Moghaddam (2014) developed a branch-and-bound algorithm that considered the setup time and assembly operations to minimize the makespan for HFSP. Sun and Yu (2015) deal with a two-stage HFSP with batch constraints and the variable processing times through a Lagrangian relaxation approach. However, because of their NP-hard nature, exact approaches are only applicable to small-scale problems. Thus, heuristic algorithms are widely used to obtain good approximations within a reasonable time (Ribas, Leisten, & Framiñan, 2010). Examples of such heuristic algorithms are the neighborhood search, simulated annealing, and genetic algorithms (GAs).

خلاصه

1. معرفی:

2. بررسی نوشته های وابسته به حرفه علمی.

3. تعریف مساله.

3.1. محدودیت های مشخص.

3.2. یک مثال توضیحی و روشن کننده.

4. الگوریتم مطرح شده.

4.1. مرحله الگوریتم NEH.

4.2. مرحله الگوریتم ژنتیک

4.3. مرحله جستجوی محلی.

4.4. مرحله رمزگشایی کروموزوم.

5. نتایج عملی و آزمایشگاهی.

5.2. نتایج آزمایشگاهی.

Abstract

1. Introduction

2. Literature review

3. Problem definition

3.1. Distinguishing constraints

3.1.1. Nighttime work

3.1.2. Simultaneous work

3.2. An illustrative example

4. Proposed algorithm

4.1. NEH algorithm phase

4.2. Genetic algorithm phase

4.2.1. Chromosome representation

4.2.2. Initial population

4.2.3. Crossover

4.2.4. Mutation

4.3. Local search phase

4.4. Chromosome decoding phase

4.4.1. Machine allocation rule

4.4.2. Fitness function

4.4.3. Selection

4.4.4. Stopping criterion

5. Experimental results

5.1. Experiment design

5.2. Experimental results

6. Conclusion and future work

Acknowledgments

References