دانلود رایگان مقاله مجموعه مستقل ماکسیمال سریع حافظه توزیع شده

چکیده

       مسئله گراف مجموعه مستقل ماکسیمال (که به اختصار MIS نامیده می‌شود) در بسیاری از برنامه‌های کاربردی نظیر بینایی کامپیوتر ، نظریه اطلاعات ، زیست‌شناسی مولکولی  و زمانبندی ظاهر شده است. مقیاس در حال رشد مسائل MIS پیشنهاد استفاده از سخت‌افزار حافظه توزیع‌شده را به عنوان روشی مقرون به صرفه برای ارائه محاسبات لازم و منابع حافظه را می‌دهد. لوبی  چهار الگوریتم تصادفی برای حل مسئله MIS ارائه کرده است. تمامی این الگوریتم‌ها با تمرکز بر دستگاه‌های حافظه مشترک طراحی شده‌اند و با استفاده از مدل PRAMمورد تجزیه و تحلیل قرار گرفته‌اند. این الگوریتم‌ها دارای پیاده‌سازی‌های کارآمد مستقیم حافظه توزیع‌شده نیستند. در این مقاله، ما دو مورد از الگوریتم‌های  MISبدوی لوبی را برای اجرای حافظه توسعه‌یافته گسترش خواهیم داد که نام آن‌ها Luby (A)و Luby(B)است و عملکرد آن‌ها را ارزیابی می‌کنیم. ما نتایج خود را با پیاده‌سازی «MISفیلتر‌شده » در کتابخانه Combinatorial BLASبرای دو نوع ورودی از گراف‌های مصنوعی مقایسه کردیم. 

1. مقدمه

          G = (V, E) را به عنوان گرافی در نظر بگیرید که در آن V نشان‌دهنده مجموعه‌ای از راس‌ها و E نشان‌دهنده مجموعه‌ای از یال‌ها است. یک مجموعه مستقل درGمجموعه‌ای از رئوسی در یک گراف است که هیچ دو راسی در مجموعه، مجاور نیستند. بزرگترین مجموعه‌های مستقل (که ممکن است بیش از یک باشد) ماکسیمم مجموعه‌های مستقل نامیده می‌شود. بنابراین یافتن ماکسیمم مجموعه مستقل ان‌پی-سخت  است، اکثر برنامه‌های کاربردی برای یافتن یک مجموعه مستقل ماکسیمال تنظیم شده‌اند. یک مجموعه مستقل ماکسیمال (MIS) از یک گراف یک مجموعه مستقل است که زیرمجموعه‌ای از مجموعه مستقل دیگر نیست (شکل 1 را ببینید). یافتن یک MIS یک مسئله مهم گراف است زیرا در بسیاری از برنامه‌های کاربردی از جمله بینایی کامپیوتر، نظریه اطلاعات، زیست‌شناسی مولکولی و زمانبندی فرآیند ظاهر شده است. اگرجه الگوریتم‌های موثر MISشناخته شده‌اند[1]، مقیاس در حال افزایش برنامه‌های کاربردی حساس به داده پیشنهاد استفاده از سخت‌افزار حافظه توزیع‌شده (خوشه‌ها ) را می‌دهد، که به نوبه خود نیاز به الگوریتم‌های توزیع حافظه دارند.

            از الگوریتم‌های MIS، لوبی مونت کارلو  [2] برای پیاده‌سازی MIS به شکل موازی استفاده می‌شود. الگوریتم‌های MIS لوبی با تمرکز بر دستگاه‌های حافظه مشترک طراحی شده‌اند و با استفاده از مدل دستگاهی با دسترسی تصادفی موازی PRAMمورد تجزیه و تحلیل قرار گرفته‌اند. الگوریتم‌های لوبی بلافاصله خود را به الگوریتم‌های موازی توزیع شده موثر قرض نمی‌دهند زیرا ممکن است سربار در اثر هماهنگ‌سازی و محاسبات زیرگراف توزیع‌شده رخ دهد. در این مقاله، نسخه‌های توزیع‌شده الگوریتم‌های لوبی مونت کارلو (الگوریتم A و B) ارائه شده است که سبب به حداقل‌رسانی این سربارها می‌شود. علاوه بر این، ما یک متغیر از Luby (A)را مشتق کرده‌ایم که از تکرار محاسبه اعداد تصادفی در هر تکرار جلوگیری می‌کند. تمامی الگوریتم‌ها در زمان اجرای AM++[3] پیاده‌سازی شده‌اند و عملکرد آن‌ها ارزیابی شده است. نتایج ما نشان‌ می‌دهد که الگوریتم‌های پیشنهادی به خوبی در تنظیمات توزیع‌شده قرار می‌گیرد. ما همچنین نتایج خود را با پیاده‌سازی MISفیلترشده در کتابخانه Combinatorial BLASمقایسه کرده‌ایم [4] و نشان داده‌ایم که پیاده‌سازی‌های ما چندین برابر سریع‌تر از الگوریتم MISفیلترشده است.

2.  کارهای مرتبط

           اکثر الگوریتم‌های MIS موازی بر روی حافظه اشتراکی تمرکز داشتند، و از مدل PRAM برای تجزیه و تحلیل پیچیدگی موازی استفاده می‌کردند (برای مثال [5]، [6]، [7]، [8]،[9]، [10] ). در این کار، ما به طور خاص بر روی الگوریتم‌های تصادفی لوبی [2] تمرکز کرده‌ایم (برای جزئیات بیشتر به بخش 3 مراجعه کنید). لوبی یک تحلیل دقیق از الگوریتم‌های خود را با استفاده از مدل دستگاهPRAM ارائه کرد. بعدها، مفاهیم الگوریتم لوبی به منظور پیاده سازی نسخه‌های توزیع‌شده مورد استفاده قرار گرفت. لینچ  و همکاران [11] در مورد یک نسخه توزیع‌شده از الگوریتم لوبی برای شبکه‌های توزیع همزمان را مورد بررسی قرار دادند. متی‌ویر  و همکاران [12] یک نسخه بهبودیافته از الگوریتم لینچ را ارائه دادند که در آن پیچیدگی پیام ارتباطی بهبود یافته بود. کوهن  و همکاران [13] یک الگوریتمMIS توزیع شده قطعی را ارائه دادند. با این حال، آن‌ها یک مدل ارتباطی همزمان را در نظر گرفتند و هیچگونه نتیجه تجربی ارائه نکردند.

            کتابخانه Combinatorial BLAS[4]یک نسخه توزیع‌شده از الگوریتم لوبی را پیاده‌سازی کرده است. این پیاده‌سازی از عناصر اولیه جبر خطی در پیاده‌سازی الگوریتم لوبی استفاده می‌کرد و همچنین این الگوریتم بر روی گراف‌های فیلترشده نیز کار می‌کرد [14]. سالیهگلو  و همکاران [15] یک نسخه توزیع شده از الگوریتم لوبی را برای سیستم‌های Pregel مانند اجرا کردند. آن‌ها از الگوریتم MIS برای حل مشکل رنگ‌آمیزی گراف استفاده کردند. گاریملا  و همکاران [16] عملکرد پیاده‌سازی لوبی در Pregel را با یک الگوریتم موازی که توسط بللوچ  و همکاران [10] طراحی شده بود مقایسه کردند. بللوچ و همکاران، الگوریتم MIS با ترتیب الفبایی اول که دارای ترتیبی حریصانه بود را موازی کردند. این الگوریتم از DAGاولیتی بر روی راس‌های گراف ورودی استفاده می‌کردند که یال‌های DAF نقاط پایانی اولویت بالاتر را به نقاط پایانی اولیت پایین‌تر بر اساس مقادیر تصادفی تخصیص یافته به راس‌ها متصل می‌کرد.

           بر روی مساله MIS موازی در بیشتر تحقیقات نظری تمرکز شده بود. بخشی از کار مرتبطی که در بالا مورد بحث واقع شد شامل تحلیل پیچیدگی زمانی موازی یا پیچیدگی کمی الگوریتم است. پیاده‌سازی‌های موجود از MIS موازی عمدتا از الگوریتم لوبی استفاده می‌کنند یا اینکه آن‌ها از الگوریتمی بر اساس MIS لوبی استفاده کرده‌اند. با این حال، MIS لوبی به سرعت به الگوریتم موازی توزیع حافظه موثر گسترش پیدا نمی‌کند دلایل این موضوع هم در بخش 3 مورد بحث قرار خواهد گرفت. 

         پیاده‌ سازی توزیع شدهMIS  لوبی درکتابخانهCombBLASبه طور آزادانه در دسترس است. بااین حال،الگوریتمCombBLASبرای فعالیت بررویگراف‌های «فیلترشده» طراحی شده است. علاوه براین،چندین پیش‌پردازش از جمله حذفیال‌های خودومتعادل‌سازی بار را نیز انجام می‌دهد. الگوریتم های لوبی توزیع شده که در این مقاله ارائه می‌شوند به طور خاص برای پردازش گرافهای ایستا در مقیاس بزرگ تحت تنظیمات حافظه توزیع شده طراحی شده‌اندو قادر به پردازش گراف‌های بدون ساختار بدون پیش ‌پردازش هستند.

3. الگوریتم‌های لوبی

           الگوریتم‌های لوبی از جمله پر استفاده‌ترین الگوریتم‌ها برای یافتن MIS در حافظه مشترک هستند. لوبی در انتشار اولیه الگوریتم خود در مورد یک طرح تکرارشونده کلی و چهار تغییرات خاص بر اساس آن بحث کرد. طرح کلی تکرارشونده در الگوریتم 1 ذکر شده است، در کل این طرح یک مجموعه مستقل غیرتهی را انتخاب می‌کند (خط5) و آن را با خروجی‌ها (Smis) ادغام می‌کند. سپس، مجموعه مستقلی که انتخاب شده است و همسایه‌های آن از گراف ورودی حذف می‌شوند و زیرگراف حاصل از آن برای تکرار بعدی طرح مورد استفاده قرار می‌گیرد (خطوط 7 الی 9). این فرآیند تا زمانی تکرار می‌شود که زیرگراف حاصل خالی باشد. در هر بار تکرار، طرح کلی تکرارشونده یک مجموعه مستقل جدید را تولید می‌کند. لوبی ثابت کرد است که اجتماع تمامی آن مجموعه‌های مستقل یک مجموعه مستقل ماکسیمال است.

            برای انتخاب یک مجموعه مستقل از یک زیرگراف در یک تکرار، لوبی دو الگوریتم مونت کارلو را ارائه کرده است که نام آن‌ها: Select A و Select B است. Select B بیشتر برای بهبود ایجاد دو متغیر بیشتر، Select C و Select D مورد استفاده قرار می‌گیرد. تمامی این چهار متغیر از تصادفی‌سازی برای محاسبه یک مجموعه مستقل استفاده می‌کنند. الگوریتم‌های ASelect و BSelect و CSelect غیرقطعی است، در حالیکه Select D قطعی است. در این مقاله، ما بر روی ASelect و BSelect تمرکز کردیم (زیرا C و D متغیرهایی از B هستند). الگوریتم‌های ASelect و BSelect در جدول 1 خلاصه شده‌اند.

Abstract

         The Maximal Independent Set (MIS) graph problem arises in many applications such as computer vision, information theory, molecular biology, and process scheduling. The growing scale of MIS problems suggests the use of distributed-memory hardware as a cost-effective approach to providing necessary compute and memory resources. Luby proposed four randomized algorithms to solve the MIS problem. All those algorithms are designed focusing on shared-memory machines and are analyzed using the PRAM model. These algorithms do not have direct efficient distributed-memory implementations. In this paper, we extend two of Luby’s seminal MIS algorithms, “Luby(A)” and “Luby(B),” to distributed-memory execution, and we evaluate their performance. We compare our results with the “Filtered MIS” implementation in the Combinatorial BLAS library for two types of synthetic graph inputs.

I. INTRODUCTION

          Let G = (V, E) be a graph where V represents the set of vertices and E represents the set of edges in the graph. An independent set in G is a set of vertices in a graph such that no two vertices in the set are adjacent. The largest independent sets (there may be more than one) are called the maximum independent sets. Since finding a maximum independent set is NP-hard, most applications settle for finding a maximal independent set. A maximal independent set (MIS) of a graph is an independent set that is not a subset of any other independent set (see Figure 1). Finding a MIS is an important graph problem used in many applications, including computer vision, coding theory, molecular biology and process scheduling. Although efficient MIS algorithms are well-known [1], the increasing scale of data-intensive applications suggests the use of distributed-memory hardware (clusters), which in turn requires distributed-memory algorithms.

         Luby’s Monte Carlo[2] MIS algorithms are often used for parallel MIS implementations. Luby MIS algorithms are designed focusing on shared memory machines and analyzed using the Parallel Random Access Machine (PRAM) model. Luby’s algorithms do not immediately lend itself to efficient distributed memory parallel algorithms due to overhead incurred by synchronization and distributed subgraph computations. In this paper, we present distributed versions of Luby’s Monte Carlo algorithms (Algorithm A and Algorithm B) that minimize these overheads. Furthermore, we derive a variation of Luby(A) that avoids computing random numbers in every iteration. All presented algorithms are implemented in the AM++ runtime [3] and their performance is evaluated. Our results show that the proposed algorithms scale well in distributed settings. We also compare our results with the FilteredMIS implementation in the Combinatorial BLAS library [4], and we show that our implementations are several times faster compared to FilteredMIS algorithm.

II. RELATED WORK

        Most parallel MIS algorithms focus on shared memory, using the PRAM model for parallel complexity analysis (e.g., [5], [6], [7], [8], [9], [10]). In this work, we specifically focus on Luby’s [2] randomized algorithms (see Section III for details). Luby provided a detailed analysis of his algorithms using the PRAM machine model. Later, Luby’s algorithm concepts were used to implement distributed versions. Lynch et al. [11] discuss a distributed version of Luby’s algorithm for synchronous distributed networks. Metivier et al. [ ´ 12] present an improved version of Lynch’s algorithm, improving communication message complexity. Kuhn et al. [13] provide a deterministic distributed MIS algorithm. However, they assume a synchronous communication model and provide no experimental results.

         The Combinatorial BLAS library[4] implements a distributed version of Luby’s algorithm. Their implementation uses linear algebra primitives in implementing Luby’s algorithm and also the algorithm works on filtered graphs[14]. Salihoglu et al. [15] implemented a distributed version of Luby’s algorithm for Pregel-like systems. They used Luby’s MIS algorithm to solve the graph coloring problem. Garimella et al. [16] compare the performance of Luby’s implementation in Pregel with a parallel algorithm designed by Blelloch et al. [10]. Blelloch et al., parallelize the sequential greedy lexicographically-first MIS algorithm. This algorithms uses a priority DAG constructed over the vertices of the input graph, where the DAG edges connect higher-priority to lower-priority endpoints based on random values assigned to vertices.

         The problem of parallel MIS has been the focus of much theoretical research. Part of the related work discussed above involves analyzing parallel time complexity or bit complexity of the algorithm discussed. Existing implementations of parallel MIS mostly adopt Luby’s algorithms or they use an algorithm based on Luby’s MIS. However, Luby’s MIS does not immediately extend to efficient distributed memory parallel algorithm due to reasons we discuss in Section III.

         A distributed implementation of Luby’s MIS is openly available in CombBLAS library. However, CombBLAS algorithm is designed to work on “filtered” graphs. Further, it performs several pre-processing steps including removing self-edges and load balancing. The distributed Luby algorithms we present in this paper are designed specifically for large-scale static graph processing under a distributed memory setting and capable of processing unstructured graphs without preprocessing.

III. LUBY’S ALGORITHMS

         Luby’s algorithms are the most widely used parallel algorithms for finding a MIS in shared memory. In his original publication, Luby discussed a general iterative scheme and four particular variations based on it. The general iterative scheme is listed in Algorithm 1. In every iteration, the general iterative scheme selects a non-empty independent set (Line 5) and merges it to the output (Smis). Then, the selected independent set and its neighbors are removed from the input graph, and the resulting subgraph is fed into the scheme for the next iteration (Lines 7– 9). This process is repeated until the resulting subgraph is empty. In every iteration, the general iterative scheme generates a new independent set. Luby proved that the union of all those independent sets is a maximal independent set.

       To select an independent set from a subgraph in an iteration, Luby proposed two Monte Carlo algorithms: Select A and Select B. Select B is further enhanced to create two more variations, Select C and Select D. All four of those variations use randomization to calculate an independent set. Select algorithms A, B, and C are non-deterministic, while Select D is deterministic. In this paper, we focus on Select algorithms A and B (since C and D are variations of B). Select A and Select B algorithms are summarized in Table I.

چکیده

1.مقدمه

2.  کارهای مرتبط

3. الگوریتم‌های لوبی

A. الگوریتم لوبی در حافظه توزیع‌شده

4. الگوریتم‌های حافظه توزیع‌شده موازی لوبی 

A. طرح تکرارشونده توزیع کلی 

B. Select A توزیع‌شده

C. انتخاب AV (یک دگرگونی از Select A).

D. SelectB توزیع‌شده

5. آزمایش‌ها و نتایج

A. پیاده‌سازی

B. تنظیمات آزمایش

C ورودی گراف

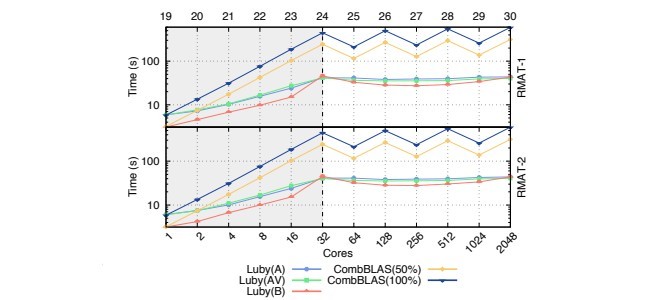
D نتایج پیمایش ضعیف

E. نتایج پیمایش قوی

6. نتیجه‌گیری

منابع

Abstract

1. INTRODUCTION

2. RELATED WORK

3. LUBY’S ALGORITHMS

A. Luby’s Algorithms in Distributed Memory

4. DISTRIBUTED MEMORY PARALLEL LUBY ALGORITHMS

A. Distributed General Iterative Scheme

B. Distributed Select A

C. Select AV (A variation of Select A)

D. Distributed Select B

5. EXPERIMENTS & RESULTS

A. Implementation

B. Experimental Setup

C. Graph Input

D. Weak Scaling Results

E. Strong Scaling Results

6. CONCLUSIONS

REFERENCES