دانلود رایگان مقاله الگوریتم یادگیری بهینه سازی جستجوی عقبگرد و کاربردهای آن

چکیده

           الگوریتم جستجوی عقبگرد (BSA) پیشنهادی در این مقاله، یک الگوریتم تکاملی (EA) می باشد که برای حل مسائل بهینه سازی استفاده می شود. ساختار این الگوریتم ساده می باشد و تنها دارای یک پارامتر کنترلی است که باید تعیین شود. به منظور بهبود عملکرد همگرائی و گسترش دامنه استفاده از آن، یک الگوریتم جدید به نام  یادگیری BSA (LBSA) در این مقاله ارائه شده است. در این روش، بطور سراسری از بهترین اطلاعات نسل حاضر و اطلاعات پیشین در BSA ، برای گزینش مجدد افراد باتوجه به احتمال تصادفی ترکیب می شوند و افراد باقی مانده موقعیت خود را توسط یادگیری دانش در بهترین فرد، بدترین فرد و یک فرد تصادفی از نسل حاضر دوباره انتخاب می کنند. دو مزیت مهم برای این الگوریتم وجود دارد. 1) بعضی از افراد موقعیت خود را با هدایت بهترین فرد ( آموزش دهنده ) بروزرسانی می کنند،که باعث همگرائی سریعتر می شود، 2) یادگیری از افراد متفاوت، بطور ویژه زمانی که بدترین فرد نادیده گرفته می شود، تنوع جمعیت را افزایش می دهد. برای آزمایش بهترین عملکرد LBSA، توابع سنجشی در CEC2005 و CEC2014 مورد آزمایش قرار گرفتند و این الگوریتم به منظور آموزش شبکه های عصبی برای پیش بینی سری های زمانی بی نظم و مشکلات مدلسازی سیستم های غیرخطی استفاده می شود. برای ارزیابی عملکرد BSA با بعضی از EAهای دیگر، چند مقایسه بین LBSA و دیگر الگوریتم های کلاسیک انجام شده است. نتایج نشان می دهند که LBSA با توجه به الگوریتم های دیگر عملکرد خوبی دارد و باعث بهبود عملکرد الگوریتم BSA می شود.

1. مقدمه

            برخی از مشکلات علوم و مهندسی حل مسائل بهینه سازی می باشد، که امروزه محققان در تلاش برای جستجو و طراحی الگوریتم های بهینه سازی بهتر می باشند. برای حل مسائل پیچیده مانند توابع غیرخطی، مشتق ناپذیر و تابع هدف غیر- محدب، محققان بر طراحی الگوریتم های تکاملی (EA) جدید یا بهبود عملکرد الگوریتم های موجود متمرکز شده اند. از این الگوریتم ها، الگوریتم بهینه سازی هوش جمعی و الگوریتم های تکامل ژنتیکی در حل مسائل پیچیده بهینه سازی نقش بسیار مهمی دارند. الگوریتم بهینه سازی ازدحام ذرات (PSO) [12]، که به تقلید از جستجوی پرندگان می باشد، در استفاده برای بهینه سازی توابع [37] ، مسائل طبقه بندی شده ترتیبی [36] و سیستم های تولید برق [25] عملکرد خوبی دارد. برخی از انواع روش های PSO، مانند روش ازدحام ذرات کاملا آگاه (PSOFIPS) [20]، PSO مبتنی بر نسبت فاصله برازش (PSOFDR) [23] و یادگیری جامع ازدحام ذرات (CLPSO) [15]، می باشند که برای بهبود عملکرد الگوریتم PSO و حل مسائل بهینه سازی پیشنهاد شده اند. علاوه بر این، برخی از الگوریتم های ترکیبی نیز برای بهبود عملکرد الگوریتم PSO [13,21] معرفی شده اند و همچنین برخی روش های گسسته برای گسترش دامنه کاربرد الگوریتم PSO [2,8,10] پیشنهاد شده است. شبیه سازی فرآیند آموزش-یادگیری در الگوریتم بهینه سازی مبتنی بر یادگیری-آموزش (TLBO) [31] نیز ارائه شده است. در این روش پارامترهای کمتری وجود دارند که باید در معادلات بروزرسانی تعیین شوند، که این کار باعث می شود الگوریتم به آسانی اجرا شود. برای استفاده کامل از مزایای الگوریتم TLBO، دو روش در نظر گرفته شده است: یکی از این روش ها بهبود کارایی الگوریتم توسط تغییر فرآیند بروز رسانی یا ترکیب آن با دیگر EAها و از سوی دیگر گسترش دامنه های کاربردی آن است. طرح نخبه گرایی که در الگوریتم نخبه گرایی TLBO (ETLBO) استفاده شده است برای بهبود عملکرد خود برخی از بدترین یادگیرنده ها را در گروه هایی توسط نخبه های دیگر جایگزین می کند[29]. یک TLBO خود یادگیر که یک روش خود یادگیری جدید می باشد برای آموزش مدلسازی عصبی تابع پایه شعاعی (RBF) باتری ها استفاده شده است[41]. بسیاری از آموزش دهندها، از عامل آموزش تطبیقی، خودآموز آموزشی و یادگیری خود انگیزشی برای بهبود تنوع جمعیت استفاده می کنند[30]. الگوریتم اصلاح شده TLBO عملکرد خوبی برای انجام برخی از مسائل بهینه سازی داشته است. باتوجه به زمینه های کاربردی، عملگر جهش لِوی(Levy) [7] برای کمک به جلوگیری از بوجود آمدن نقطه بهینه محلی TLBO استفاده شده است و الگوریتم جدید با موفقیت برای سیستم IEEE سی شینه استفاده شده است. TLBO بهبود یافته[6] در جهتی یکسو برای افزایش توانایی جستجوی آموزش دهنده ها معرفی شده است که با یک الگوریتم تکاملی تفاضلی دوطرفه برای کنترل مسئله پخش بار بهینه توان راکتیو (ORPD) ترکیب شده است. روش های محلی و خود یادگیر [3] به منظور بهبود عملکرد TLBO ابتکاری استفاده شده است، این روش ها عملکرد خوبی از خود برای مسائل بهینه سازی سراسری نشان می دهند. بهینه سازی مبتنی بر آموزش-یادگیری چند هدفه[19] برای کنترل توان راکتیو سیستم ها استفاده می شود. بهینه سازی مبدل های حرارتی صفحه ای-پره دار[22] و فرآیندهای ماشینکاری مدرن [28]، مشکلات بهینه سازی برنامه ریزی واحدهای حرارتی آبی بلند مدت[32]، بهینه سازی سرد کن های حرارتی دو مرحله ای[27] و مشکلات برنامه ریزی دوباره خط تولید [11,14]  توسط الگوریتم بهینه سازی TLBO حل شده اند. بررسی دقیق برنامه های کاربردی TBLO را می توان در مقاله [26] یافت. ساده سازی فرآیند آموزش و کاهش تعداد پارامترهای نامعین الگوریتم های بهینه سازی هوشمند موضوع بسیار مهمی می باشد. برای پرداختن به این موارد، یک الگوریتم جدید به نام الگوریتم جستجوی عقبگرد (BSA)[5] در سال 2013 پیشنهاد شده است که برای برخی از مشکلات بهینه سازی مهندسی استفاده می شود. الگوریتم BSA برای تجزیه و تحلیل موج سطحی [34] و برای حل مسائل بهینه سازی ترکیب آرایه های آنتن مدور متحدالمرکز استفاده می شود[9]. BSA و الگوریتم تکامل تفاضلی (DE) را می توان برای حل مسائل بهینه سازی بدون محدودیت باهم ترکیب نمود[40]. الگوریتم BSA مقابله ای [17] برای حل مسائل بهینه سازی، شناسایی پارامتر سیستم های فوق آشوبی معرفی شده است. الگوریتم BSA با سه روش کنترل محدودیت [43] برای حل مسائل بهینه سازی که دارای محدودیت می باشند استفاده می شود. برای برخی از EAهای کلاسیک، BSA الگوریتم بهینه سازی بسیار جدیدی می باشد و از طرفی نوع بهبود یافته الگوریتم BSA به نسبت کم تر مورد تحلیل قرار گرفته است.

            همانطور که در بالا ذکر شده است، BSA و TLBO هر دو نشان دادند که در حل برخی از مسائل بهینه سازی بهتر از الگوریتم های دیگر می باشند، بویژه به دلیل آنکه الگوریتم ها ساده هستند و پارامترهای نامعین کمی در معادلات بروزرسانی فردی وجود دارد. از طرفی عملکرد الگوریتم های نوین در حل مسائل پیچیده نیاز به بهبود دارد. معایب این الگوریتم ها در بخش های 2 و 3 بصورت دقیق تر آمده است.

           برای بهبود عملکرد سراسری الگوریتم BSA ، یک روش جدید که ترکیبی از ایده های TLBO و BSA می باشد در این مقاله ارائه شده است. بخش اصلی روش جدید به شرح زیر می باشد. بخش اول علاوه بر هدایت یادگیری در معادلات بروزرسانی BSA سرعت همگرایی BSA را بهبود می بخشد. بخش دوم برای ادغام سه روش یادگیری در یک معادله به منظور بروزرسانی افراد باتوجه به احتمالات تصادفی است. یکی دیگر از بخش ها اجتناب از استفاده بدترین فرد در جهت بهبود تنوع یا گوناگونی جمعیت می باشد. در مقابل برای دو تابع ارزیابی (FE) برای یک فرد در یک نسل از الگوریتم TLBO، تنها یک FE در هر نسل برای روش جدید وجود دارد. از این رو، هزینه محاسبات برای یک نسل از الگوریتم پیشنهادی نسبت به TLBO کمتر است.

          بقیه مقاله به شرح زیر می باشد: BSA بنیادی و TLBO ابتکاری بطور مختصری به ترتیب در بخش 2 و بخش 3 معرفی شده اند؛ LBSA در بخش 4 اراده شده است؛ توابع سنجشی در CEC2005 و CEC2014 برای نشان دادن اثر الگوریتم های مختلف در بخش 5 آزمایش شده اند؛ برنامه های کاربردی برای دو مشکل مدلسازی غیرخطی و مشکلات پیش بینی سری های زمانی آشوبی در بخش 6 نمایش داده شده است و در نهایت نتیجه گیری در بخش 7 آمده است.

2. BSA بنیادی 

            BSA یک EA مبتنی بر جمعیت است که با استفاده از الگوریتم DE توسعه یافته است، اما شبیه به الگوریتم DE نمی باشد. این الگوریتم شامل 5 فرآیند می باشد: مقدار دهی اولیه، گزینش-1 ، جهش، ترکیب و گزینش-2. دو تنوع جمعیتی در BSA وجود دارد: یک از آنها جمعیت تکاملی و دیگری جمعیت آزمایشی می باشد. جمعیت آزمایشی از برخی اطلاعات پیشین جمعیت تکاملی تشکیل شده است و یک ماتریس جستجوی جهت دار توسط دو جمعیت برای بروزرسانی موقعیت افراد ایجاد می شود. تنها یک پارامتر کنترل، یعنی نرخی ترکیبی وجود دارد، که تعداد عناصر فردی را کنترل می کند و در یک آزمایش جهش می یابد. پنج مرحله از BSA به شرح زیر می باشد و جزئیات بیشتر آن در مقاله [5] بیان شده است.

          همانطور که در مقدمه ذکر شد، BSA الگوریتمی با ساختار ساده تر نسبت به برخی از EA ها، مانند PSOها، الگوریتم ژنتیگ و DEها می باشد. ترکیب و مکانیزم جهش از الگوریتم DE و انواع آن متفاوت می باشند. اطلاعات پیشین در فرآیند بروز رسانی برای بهبود عملکرد الگوریتم استفاده می شوند. با این حال، به عنوان یک الگوریتم نوین، BSA نیز معایبی دارد. اولین عیب آن نبودن هیچ هدایت کننده ای به عنوان بهترین فرد در فرآیند بروز رسانی می باشد که می تواند باعث سرعت همگرائی آهسته BSA شود. دومین عیب BSA، زمانی می باشد که تنوع جمعیت از بین رفته و افرد نمی توانند دوباره انتخاب شوند، زیرا جمعیت آزمایشی هنگامی که جمعیت تقریبا شبیه به نسل بعدی است ممکن نیست تغییر کند. این امر باعث کاهش توانایی BSA برای جلوگیری از ایجاد نقطه بهینه محلی می شود.

Abstract

           The backtracking search algorithm (BSA) is a recently proposed evolutionary algorithm (EA) that has been used for solving optimisation problems. The structure of the algorithm is simple and has only a single control parameter that should be determined. To improve the convergence performance and extend its application domain, a new algorithm called the learning BSA (LBSA) is proposed in this paper. In this method, the globally best information of the current generation and historical information in the BSA are combined to renew individuals according to a random probability, and the remaining individuals have their positions renewed by learning knowledge from the best individual, the worst individual, and another random individual of the current generation. There are two main advantages of the algorithm. First, some individuals update their positions with the guidance of the best individual (the teacher), which makes the convergence faster, and second, learning from different individuals, especially when avoiding the worst individual, increases the diversity of the population. To test the performance of the LBSA, benchmark functions in CEC2005 and CEC2014 were tested, and the algorithm was also used to train artificial neural networks for chaotic time series prediction and nonlinear system modelling problems. To evaluate the performance of LBSA with some other EAs, several comparisons between LBSA and other classical algorithms were conducted. The results indicate that LBSA performs well with respect to other algorithms and improves the performance of BSA.

1. Introduction

          For some science and engineering problems that can be converted to optimisation problems, the search for and design of better optimisation algorithms has never ceased. To solve complex problems such as nonlinear, non-differentiable, and non-convex objective function problems, researchers have focused on designing novel evolutionary algorithms (EAs) or improving the performance of existing algorithms. Of these algorithms, swarm intelligence optimisation algorithms and genetic evolution algorithms play very important roles in the solution of complex optimisation problems. The particle swarm optimisation (PSO) algorithm [12], which mimics the foraging law of birds, has been successfully used in function optimisation [37], sequence classification problems [36], and power output systems [25]. Some variants of PSO, such as the fully informed particle swarm (PSOFIPS) [20], fitness-distance-ratio-based PSO (PSOFDR) [23], and comprehensive learning particle swarm (CLPSO) [15], have also been proposed to improve the performance of PSO and solve optimisation problems. Moreover, some hybrid algorithms are also introduced to improve the performance of PSO [13,21], and some discrete methods are proposed to extend the application domain of PSO [2,8,10]. Simulating the teaching-learning process in a class, the teaching-learning– based optimisation (TLBO) algorithm [31] has also been proposed. There are fewer parameters that must be determined in its updating equations, and the algorithm is easily implemented. To make full use of the advantages of TLBO, two approaches have been taken: one is to improve the efficiency of the algorithm by modifying the updating process or combining it with other EAs, and the other is to extend its application domains. The concept of elitism has been utilised in elitism TLBO (ELTBO) to improve its performance by replacing some worst learners in the class by elitisms [29]. A self-learning TLBO that designs a new self-learning method has been used to train the radial basis function (RBF) neural modelling of batteries [41]. Many teachers, an adaptive teaching factor, tutorial training, and self-motivated learning have all been used to improve the diversity of the population [30]. These modified TLBO algorithms perform well for some optimisation problems. With respect to the application fields, the Lévy mutation operator [7] has been used to help TLBO avoid local optima, and the new algorithm has successfully been used for the IEEE 30-bus test system. An improved TLBO [6] with direction angle has been introduced to increase the searching ability of its learners, and it has been combined with a double differential evolution algorithm to handle the optimal reactive power dispatch (ORPD) problem. Local and self-learning methods [3] have been used to improve the performance of the original TLBO, and these approaches display some good performance for global optimisation problems. The multi-objective teaching-learning optimiser [19] has been used for handling reactive power systems. The optimisation of plate-fin heat exchangers [22] and modern machining processes [28], short-term hydrothermal scheduling problems [32], two-stage thermoelectric coolers [27], and flow-shop rescheduling problems [11,14] have all been solved by TLBO. A detailed review of applications of TLBO can be found in [26]. Simplifying the training process and decreasing the number of undetermined parameters of intelligence optimisation algorithms are very important issues. To address them, a novel algorithm called the backtracking search algorithm (BSA) [5] was proposed in 2013 and used for some engineering optimisation problems. BSA has been used for surface wave analysis [34] and to solve concentric circular antenna array synthesis optimisation problems [9]. BSA and differential evolution algorithm (DE) have also been combined to solve unconstrained optimisation problems [40]. The oppositional BSA [17] was introduced to solve hyper-chaotic system parameter identification optimisation problems. The BSA with three constraint handling methods [43] was used for solving constrained optimisation problems. Compared to some classical EAs, BSA is a very new optimisation algorithm, and the improved variants of BSA are relatively few.

         As mentioned above, BSA and TLBO have both shown to be superior at solving some optimisation problems, especially because the algorithms are simple and there are few undetermined parameters in the individual updating equations. As young algorithms, their performance at solving complex problems needs to be improved. Their disadvantages are detailed in Sections 2 and 3.

          To improve the global performance of BSA, a new method that combines the ideas of TLBO and BSA is presented in this paper. The main contributions of the new method are as follows. The first contribution is the addition of learning guidance in the BSA updating equations to improve convergence speed of BSA. The second is the integration of three learning methods into one equation to update parts of individuals according to a random probability. Another contribution is the avoidance of the use of the worst individual in order to improve the diversity of the population. In contrast to the two function evaluations (FEs) for an individual in a generation of the TLBO algorithm, there is only one FE per generation in the new method. Hence, the computation cost for a generation of the proposed algorithm is less than that of TLBO.

           The rest of the paper is organised as follows: the basic BSA and original TLBO are briefly introduced in Section 2 and Section 3, respectively; LBSA is presented in Section 4; the benchmark functions in CEC2005 and CEC2014 are tested to show the effectiveness of different algorithms in Section 5; the applications for two typical nonlinear modelling problems and chaotic time series prediction problems are displayed in Section 6; and conclusions are given in Section 7.

2. Basic BSA

           The BSA is a population-based EA that is developed from a DE algorithm, but it is not the same as DE. It contains five processes: initialisation, selection-I, mutation, crossover, and selection-II. There are two populations in BSA: one is the evolution population and the other is the trial population. The trial population is composed of some historical information regarding the evolution population, and a search-direction matrix is built by the two populations to update the positions of the individuals. There is only one control parameter, namely the mix rate, which controls the number of individual elements that will be mutated in a trial. The five steps of BSA are simply described as follows, and further details can be found in [5].

          As mentioned in the introduction, BSA is an algorithm with a simpler structure than some EAs, such as PSOs, genetic algorithms, and DEs. The crossover and mutation mechanisms are different from those of DE and its variants. The historical information is used in the updating process to improve the performance of the algorithm. However, as a young algorithm, BSA also has some disadvantages. The first is that there is no guidance as to the best individual in the updating process, which can slow the convergence speed of BSA. The second is that individuals cannot be renewed when the diversity of the population is lost, because the trial population may not be changed when the population is almost the same in a later generation. This decreases the ability of BSA to avoid local optima.

چکیده

1 . مقدمه

2. BSA بنیادی 

3 .مراحل اصلی TLBO

3.1 مرحله آموزش دهنده

3.2 مرحله یادگیرنده

4 . LBSA

4.1 انگیزه

4.2 جهش LBSA

4.3 تجزیه و تحلیل تنوع BSA و LBSA

5 . شبیه سازی آزمایش ها

5.1 راه اندازی آزمایشی

5.2 تنظیمات پارامتر

5.3 آزمایش های CEC2005

5.3.1 مقایسه درستی راه حل تابع D 10 در CEC2005

5.3.2 مقایسه درستی راه حل تابع D 30 در CEC2005

5.3.3 مقایسه آزمون T برای D30 در CEC2005

5.4 آزمایشات برای توابع در CEC2014

5.4.1 مقایسه درستی راه حل تابع D10 در CEC2014

5.4.2 مقایسه آزمون t برای توابع در CEC2014

6 . آموزش شبکه عصبی مصنوعی 

6.1 شناسایی سیستم غیرخطی

A . سیستم غیر خطی SISO

B .  سیستم غیرخطی MISO

6.2 پیش بینی سری های زمانی آشوبی

A . سری های زمانی آشوبی مکی-گلاس (MG)

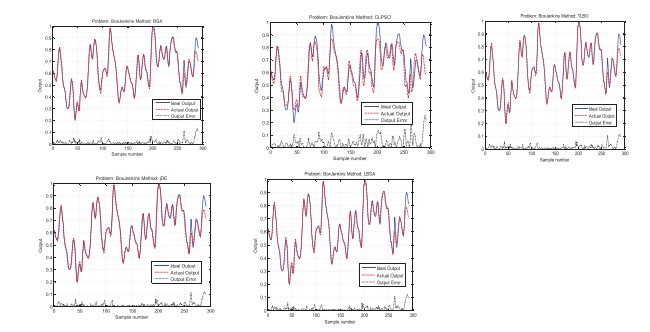
B . سری های زمانی آشوبی باکس-جنکینز

7 . نتیجه گیری 

منابع

ABSTRACT

1. Introduction

2. Basic BSA

3. Main steps of TLBO

3.1. Teacher phase

3.2. Learner phase

4. LBSA

4.1. Motivations

4.2. LBSA mutation

4.3. Diversity analysis of BSA and LBSA

5. Simulation experiments

5.1. Experimental setup

5.2. Parameter settings

5.3. CEC2005 experiments

5.3.1. Comparison of 10D function solution accuracy in CEC2005

5.3.2. Comparison of 30D function solution accuracy in CEC2005

5.3.3. T-test comparisons for 30D functions in CEC2005

5.4. Experiments for functions in CEC2014

5.4.1. Comparison of 10D function solution accuracy in CEC2014

5.4.2. T-test comparisons for functions in CEC2014

6. ANN training

6.1. Nonlinear system identification

A. SISO nonlinear system

B. MISO nonlinear system

6.2. Chaotic time series prediction

6.2. Chaotic time series prediction

A. Mackey-Glass (MG) chaotic time series

B. Box-Jenkins chaotic time series

7. Conclusions

References