دانلود رایگان مقاله مدلسازی بتن محصور در FRP با استفاده از پلاستیسیته آسیب بتن اصلاح شده

چکیده

            مدلسازی اجزای محدود (FE) ستون های بتنی محصور عملی چالش برانگیز بوده به این دلیل که نیازمند تعریف دقیق مدل مصالح بتنی به منظور ارائه رفتار حجمی بتن به حالت های تنش سه گانه است. زمانیکه بتن به وسیله ترکیبات فیبرهای پلیمری تقویت شده (FRP) محبوس می شود، مسئله پیچیده تر می شود که ناشی از ماهیت منفعل محصور کنندگی FRP است. مدل پلاستیسیته آسیب بتن (CDPM) موجود در بسته نرم افزاری اجزا محدود (ABAQUS) به طور گسترده ای به منظور مدلسازی ستونهای بتنی مسلح تحت تنش محوری مورد استفاده قرار گرفته است. با این حال، استفاده از CDPM زمانیکه به بتن محصور اعمال می شود دارای محدودیتهایی است. این مقاله به این محدودیتها اشاره کرده و مدل پلاستیسیته آسیب بتن را ارائه می کند. مجموعه جدیدی از روابط کرنش سخت شودگی/ نرم شودگی سازنده هم برای بتنی که به صورت فعال محصور شده و هم برای بتن FRP محصور شده ایجاد شده و یک مدل انبساطی به وجود آمده است. مدل انبساطی به عنوان تابعی از سختی پوشش FRP بیان می شود. CDPM اصلاح شده برای ستون هایی کاربرد دارد که دارای مقاطع عرضی متفاوت هستند، از جمله دایره ای، مربع شکل، و مستطیل شکل و محدوده گسترده ای از مقاومت های بتنی از مقاومت عادی گرفته تا مقاومت بالا را شامل می شوند. نتایج اجزا محدود ناشی از استفاده از CDPM اصلاحی ایجاد شده، تطابق خوبی را با اطلاعات به دست آمده از آزمایش ستون های بتنی محصور FRP گزارش شده در سوابق پژوهشی فنی دارد. 

1. مقدمه

          در طی دو دهه گذشته چندین کار آزمایشی و تحلیلی به منظور ارزیابی رفتار ستون های بتنی محصور شده در ترکیبات فیبرهای پلیمری تقویت شده (FRP)، زمانیکه در معرض بارگذاری فشاری محوری یکنواخت هستند انجام شده است. در نتیجه بسیاری از مدل های تنش و کرنش ایجاد شده اند، که اکثریت آن ها فرم های بسته ای بودند که بر اساس اطلاعات آزمایش موجود کالیبره شده بودند. مطالعات اخیر این مدل های موجود را بررسی و ارزیابی کردند [1-5]. ستون های بتنی محصور FRP همچنین تحت بارگذاری چرخه ای محوری و حالت ها مورد آزمایش قرار گرفتند تا که پاسخ های چرخه ای استخراج شده را نیز پیش بینی کنند [6-9]. 

          علاوه بر کارهای آزمایشگاهی و تحلیلی، تلاش های بسیاری به منظور مدلسازی ستون های بتنی محصور FRP با استفاده از روش اجزا محدود (FE) انجام شده است. اولین مزیت روش FE توانایی آن جهت مقابله با غیرخطی بودن هندسی و تعاملات مصالح مختلف است. با این حال، پیچیدگی اصلی در مدلسازی FE در تعریف صحیح مشخصات مواد (به عنوان مثال صفحات FRP و بتن) قرار دارد. صفحات FRP معمولاً به صورت مصالح الاستیک خطی مدلسازی شده اند. زمانیکه فیبرها در جهت حلقه قرار دارند، تنها ویژگی های حلقه حائز اهمیت هستند. از سوی دیگر، بسیاری از مدل های سازنده به منظور تعیین مشخصات بتن در نرم افزار FE پیشنهاد شده اند، به ویژه برای بتن هایی که در معرض فشار محصور کننده قرار دارند. تئوری پلاستیسیته به طور گسترده ای به منظور مدلسازی بتن محصور شده مورد استفاده قرار گرفته است. اولین انواع مدل های پلاستیسیته بتن بر اساس، الاستیک غیرخطی، پلاستیسیته اندو-کرونیک، پلاستیسیته کلاسیک، پلاستیسیته چند لایه و یا دارای صفحات کوچک، و پلاستیسیته سطح مرزی بود. با این حال، همان طور که توسط میمیران و همکاران  [10] گزارش گردید، این مدل ها یا دارای قابلیت های محدود بوده و یا نیازمند پارامترهای گسترده ای برای کالیبره شدن هستند.     

           اخیراً نوع دراکر- پریجر (D-P) یکی از پرکاربردترین انواع مدل های پلاستیسیته برای مدل سازی بتن محصور بوده است [11-21]. گزارشاتی که از مدل پلاستیسیته نوع D-P استفاده می کنند نتایج خوبی را در زمان پیش بینی رفتار یکنواخت بتن محصور FRP گزارش کرده اند. در میان این مطالعات، رویکرد اول روزاکیس و همکاران  [21] پیشنهاد معادلات بسته ای بود که تمامی پارامترهای مدل D-P را برای بتن یکنواخت حصور شده با FRP ارائه کردند. این پارامترها شامل تابع سخت شدگی/ نرم شدگی، تابع پتانسیل پلاستیک، پارامتر انبساط، و پارامتر آسیب هستند. معیار شکست برای تحلیل FE ستون های دایره ای نیز پیشنهاد گردید. این معیار وابستگی مقاومت بتن بر صلبیت پوشش و مدول الاستیسیته فیبرهایی که توسط بسیاری از محققان پیشنهاد شده بود را تایید کرد [1-9 و 22]. یافته های روزاسکی و همکاران [21] توسط کارابینیز و همکاران  [14] به منظور کالیبره کردن مدل D-P در دسترس در آباکوس [23] مورد استفاده قرار گرفت تا سیلندرهای و منشورهای بتنی مسلح و غیرمسلح را تحلیل کند.

           اخیراً، جیانگ و وو  [12] از نتایج آزمایشگاهی موجود در سوابق پژوهش استفاده کردند تا حالت هایی را از زاویه انبساطی بتا و زاویه اصطحکاک فی و تابع سخت شدگی/ نرم شدگی k مورد نیاز توسط مدل پلاستیسیته نوع D-P برای مدل سازی FRP محصور بتن دایره ای را ایجاد کنند. این موارد در نرم افزادر آباکوس [23] اعمال گردیده و توانستند تا پاسخ های تنش/ کرنش محوری آزمایشگاهی را برای نمونه های بتنی محصور با FRP و مقاومت عادی را به دست اورند که در معرض بارگذاری فشاری بودند. جیانگ و وو [20] از یافته های [12] استفاده کرده و از مجموعه اطلاعاتی بزرگتری برای تعیین تسلیم بتن تحت حالت های تنش سه بعدی بهره بردند. رویکرد آن ها شامل جداکردن زاویه اصطحکاکی و چسبندگی از تابع تسلیم و ایجاد مدل هایی برای پارامترهای مختلف با استفاده از نتایج فشاری بود. این تحقیق همچنین رابطه میان پارامترهای تابع تسلیم و تابع پتانسیل را مورد بررسی قرار داد و روش آزمایشی را برای ترسیم سطح تسلیم در هر زاویه اصلی ارائه کرد. 

           دیگر محققان بتن محصور در FRP را با استفاده از مدل پلاستیسیته نوع کاراگزیان و کیس  (K-C) [24] مدلسازی کردند. در سال 2010، یو و همکاران  [11] مدل های پلاستیسیته نوع D-P موجود را ارزیابی کرده و معیاری را برای تابع تسلیم، قانون سخت شدگی / نرم شدگی و قانون جریان پیشنهاد کردند که باید در مدل پلاستیسیته نوع D-P در نظر گرفته شود تا بتوان به صورت دقیق رفتار بتن محصور شده فعال و منفعل را پیش بینی کرد. مدل پیشنهادی توسط یو و همکاران دراستفاده از مدل پلاستیسیته آسیب اصلاح شده دارای محدودیت هایی بود که در مقاله همراه [25] شرح داده شده اند. این مدل بعدها توسط تنگ و همکاران  [26] بهبود داده شد تا رفتار سه بعدی FRP و آرماتورهای ستون های بتنی محصور را بگیرد. کبیر و شفایی  [27] همچنین از مدل پلاستیسیته آسیب بتن در ترکیب با پلاستیسیته ظرفیت نرم استفاده کردند تا ستون های RC دایره ای محصور FRP را مدل کنند که در معرض بارگذاری محوری غیرعادی هستند. در تحقیق جدیدی که توسط ازباکالوگلو و همکاران  [28] در طی فرایند بررسی این مقاله منتشر شد، مدل پلاستیسیته آسیب بتن اصلاحی را برای بتن محصور FRP و هم برای مقاومت های بالا و هم مقاومت های عادی ارائه کرد. 

           علاوه بر این، لو و همکاران [29] مدل FE را برای ستون های بتنی مستطیلی محصور FRP بر اساس مدل سازنده بتنی پیشنهادی توسط دانگ و همکاران  [30] و سطح شکست منتری و ویلیام  [31] ارائه کردند.

           مدل پلاستیسیته آسیب بتن (CDPM) در دسترس در آباکوس [23] که توسط لوبلینر و همکاران  [32] ایجاد شده و توسط لی و فنوز  [33] اصلاح شده نیز به صورت گسترده از مدل بتن مسلح استفاده کرده و در زمان مدل سازی بتن محصور با فشار یکنواخت و ثابت و یا بتن محصور FRP دارای محدودیت هایی است.   

Abstract

         Finite element (FE) modeling of confined concrete columns is a challenging task because it requires accurate definition of the concrete material model to represent the volumetric behavior of concrete subject to triaxial stress states. When concrete is confined by fiber-reinforced polymer (FRP) composites, the problem becomes more complex due to the passive nature of the FRP confinement. Concrete Damaged Plasticity Model (CDPM) available in the finite element software package (ABAQUS) has been widely used to model reinforced concrete columns under axial stress. However, the use of CDPM has limitations when applied to confined concrete. This paper addresses these limitations and presents a modified Concrete Damaged Plasticity Model. A new set of strain hardening/softening constitutive relationships for both actively confined concrete and FRP-confined concrete are generated and a concrete dilation model is developed. The dilation model is expressed as a function of the stiffness of the FRP-jacket. The modified CDPM is applicable to columns with different types of cross-sections, including circular, square and rectangular and large range of concrete strengths varying from normal to high strength. Finite Element results obtained using the developed modified CDPM showed a very good agreement with test data for FRP confined concrete columns reported in the technical literature.

1. Introduction

          During the last two decades, several experimental and analytical work has been carried out for evaluating the behavior of concrete columns confined with fiber reinforced polymer (FRP) composites when subjected to monotonic axial compressive loading. As a result, many stress-strain models have been developed, the majority of which were closed-form expressions calibrated based on available test data. Recent studies reviewed and assessed these available models [1–5]. FRP-confined concrete columns were also tested under axial cyclic loading and expressions to predict the cyclic response were also derived [6–9].

           Further to the experimental and analytical work, many attempts have been made to model FRP-confined concrete columns using the Finite Element (FE) method. The main advantage of the FE method is its ability to deal with geometric non-linearity and the interactions of different materials. However, the main complexity of the FE modeling lies in the proper definition of the different materials properties (i.e. FRP sheets and concrete). FRP laminates are usually modeled as linear elastic materials. When the fibers are in the hoop directions, only the hoop properties are crucial. On the other hand, many constitutive models were suggested to define concrete properties in FE software, especially for concrete subjected to confinement pressure. The theory of plasticity has been widely used to model confined concrete. The first types of concrete plasticity models were based on: nonlinear elasticity, endo-chronic plasticity, classical plasticity, multi-laminate or micro-plane plasticity, and bounding surface plasticity. However, as reported by Mirmiran et al. [10], these models are either of limited applicability or require large number of parameters to be calibrated.

          More recently, Drucker-Prager (D-P) type was one of the most used types of plasticity models for modeling confined concrete [11–21]. Studies using the D-P type plasticity model reported good results when predicting the monotonic behavior of FRP confined concrete. Among these studies, Rousakis et al. [21] was the first approach proposing closed-form equations that interrelate all the parameters of D-P model for concrete uniformly confined with FRP. These parameters included hardening/softening function, plastic potential function, dilation parameter, damage parameter. A failure criterion for FE analyses of circular columns was also proposed. This criterion validated the dependency of the concrete strength on the jacket rigidity and the fiber modulus of elasticity that was suggested by many researchers [1–9,22]. The findings of Rousakis et al. [21] were utilized by Karabinis et al. [14] to calibrate the D-P model available in ABAQUS [23] to analyze concrete cylinders and concrete prisms with or without steel reinforcement. More recently, Jiang and Wu [12] used experimental results available in the literature to generate expressions of the plastic dilation angle b, friction angle u and hardening/softening functions k required by a D-P type plasticity model for modeling FRP confined circular concrete. These expressions were implemented in ABAQUS [23] and were able to reproduce the experimental axial stressstrain responses of FRP confined normal strength concrete specimens subjected to compressive loading. Jiang and Wu [20] built on the findings of [12] and used a larger experimental database to determine the yield of concrete under a three-dimensional stress state. Their approach consisted of decoupling the friction angle and cohesion from the yield function and generating models for the different parameters using compression results. The research also studied the interrelation between the yield function and the potential function parameters and proposed a test methodology to plot the yield surface at any Lode angle.

          Other researches modeled FRP-confined concrete using a Karagozian and Case (K-C) type plasticity model [24]. In 2010, Yu et al. [11] assessed existing D-P type plasticity models and proposed criteria for the yield function, hardening/softening rule and flow rule that should be included in a D-P type plasticity model, to accurately predict the behavior of both actively and passively confined concrete. D-P model modified by Yu et al. [11] showed some limitations addressed in a companion paper [25] using modified damaged plasticity model available in ABAQUS [23]. This model was later improved by Teng et al. [26] to capture the three dimensional behavior of FRP and steel confined concrete columns. Kabir and Shafei [27] also used concrete damage plasticity combined with smooth cap plasticity to model FRP-confined circular RC columns subjected to eccentric axial loading. A recent study by Ozbakkaloglu et al. [28] published during the review process of this paper, proposed a modified concrete damaged plasticity model for FRPconfined concrete of both normal and high strengths.

         Furthermore, Lo et al. [29] proposed an FE model for FRPconfined rectangular concrete columns based on the concrete constitutive model developed by Dong et al. [30] and the failure surface of Menétrey and Willam [31].

         Concrete damaged plasticity model (CDPM) available in ABAQUS [23], developed by Lubliner et al. [32] and modified by Lee and Fenves [33], although widely used to model reinforced concrete, shows limitations when modeling either concrete confined with a constant confinement pressure or FRP-confined concrete.

چکیده

1. مقدمه

3. مدل سازی FE

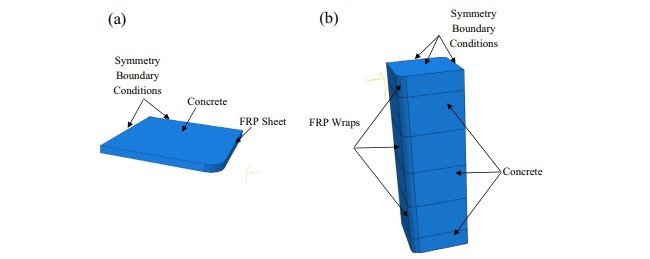
3.1 شرایط مرزی و تعاملات

3.2 نوع مولفه و مش بندی

3.3 مشخصات مواد

3.3.1 صفحات FRP

3.3.2 بتن

3.3.2.1 رفتار کششی

3.3.2.2 رفتار فشاری

3.3.2.3 پارامتر پلاستیسیته

5. مدل پیشنهادی در برابر نتایج آزمایشگاهی

6. خلاصه و نتیجه گیری

منابع

Abstract

1. Introduction

3. FE modeling

3.1. Boundary conditions and interactions

3.2. Element type and meshing

3.3. Material properties

3.3.1. FRP sheets

3.3.2. Concrete

3.3.2.1. Tensile behavior

3.3.2.2. Compressive behavior. The non-linear compressive behavior of concrete is divided into compression hardening and compression damage.

3.3.2.3. Plasticity parameters.

5. Proposed model versus experimental results

6. Summary and conclusions

References