دانلود رایگان مقاله تمام جمع کننده Coplanar در اتوماتای سلولی کوانتوم

چکیده:

     ما از یک معماری متقاطع QCA کوپلار در طراحی تمام جمع کننده QCA استفاده کردیم که منجر به کاهش تعداد سلول‌های QCA  و مصرف منطقه بدون مجازات تأخیر می‌شود. این عمل تقاطع از Clock-Zone غیر همجوار برای دو سیم عبوری استفاده می‌کند. ما در ادامه تأثیر این دستاوردها را بر روی جمع کننده جریان QCA بررسی کردیم. این طرح ها با QCADesigner تحقق یافته، ارزیابی و آزمایش شده اند. برای مقایسه عملکرد با کارهای مرتبط قبلی، ما از یک تابع هزینه QCA و همچنین روش ارزیابی معمولی استفاده کردیم. ما به بهبود 23٪ تعداد سلول و 48٪ مساحت نسبت به طراحي كامل تمام جمع کننده QCA قبلي رسیدیم. نتایج مشابهی برای افزایشگر 4- ، 8- ، 16- ، 32- و 64 بیتی بدست آمد که به ترتیب برابر با 29٪ (22٪) ، 24٪ (51٪) ، 19٪ (54٪) ، 13٪ (69٪) و 9٪ (49٪) به همراه کاهش تعداد سلول (مصرف کمتر منطقه) هستند.

1.مقدمه

     از آنجا که دستگاه های CMOS با مقیاس نانومتری با چالش های تحقق جدید روبرو هستند (به عنوان مثال، افزایش جریان نشت که منجر به اتلاف قدرت استاتیک قابل توجه می شود) [1] فن‌آوری‌های جدید به عنوان جایگزین های ممکن برای CMOS در حال ظهور هستند. اتومات های سلولی کوانتومی نقطه (QCA) [2] یکی از چنین سیستم عامل های ابتکاری را نشان می دهد. سلول اصلی QCA ، که قادر به نمایان کردن یک بیت منطقی است، منطقه ای از مقیاس نانو را اشغال می کند. یک سلول QCA بدوی معمولاً شامل دو الکترون است که دو محل دافع احتمالی کولومب [2] جایگاه‌های آن‌ها "1" و "0" است.

     درک تمام جمع کننده (FA) QCA به عنوان رایج‌ترین سلول حسابی دیجیتال، مورد توجه بسیاری از مقالات تحقیقاتی قابل ملاحظه بوده است (به عنوان مثال ، [3] [4] [5] [6] [7]). برای نشان دادن تأثیر چنین سلول حسابی بسیار سریع و کم قدرت، تمام جمع کننده QCA [3] [5] [6] [8] و ضرب کننده [6] [9] طراحی شده اند. یک مشکل در طراحی سلول‌های کامپوزیتی QCA و مدارها این است که چگونه به طور مؤثر سیم های متقاطع را برای کاهش هزینه (به عنوان مثال ، تعداد سلول‌های QCA و پیچیدگی پیاده سازی) بطور مؤثر طراحی کنیم. راه‌حل چند لایه هزینه بالایی را متحمل می شود، به عنوان مثال، مسئله ساخت [10]. گذرگاه منطقی [11] نیز به دلیل مساحت بالای آن مساعد نیست. با این حال، برای رسیدن به سیم کشی متقاطع قطبی، سلول‌های QCA چرخش 45 درجه با درجه حرارت پیشنهاد شده است [4].

     این مورد مشکلات خاص خود را دارد، مانند استحکام کم [12] و هزینه بالای اجرای آن به دلیل همزیستی دو نوع سلول QCA [10]. با این وجود، طراحی سیم متقاطع QCA از تقسیم زمان بهره می گیرد که توسط برنامه زمان‌بندی ویژه 8 فاز با سه نوع سیگنال ساعت پشتیبانی می شود [13]. این جایگزین سلولی تک نوع بسیار مقاوم و طراحی آن آسان است. با این حال، یک تکنیک اخیر [14] ، [15] که همچنین از سلول‌های یک نوع استفاده می کند، از مناطق غیر همجوار یک برنامه زمان‌بندی 4 فاز برای حل و فصل عبور سیم در یک لایه استفاده می کند.

     در این مقاله ما از تکنیک متقاطع دوم در طراحی تمام جمع کننده QCA (QFA) و افزودنی‌های جریان حمل [6] مربوطه استفاده می‌کنیم. ما ارقام عملکردی خود را با نمونه کارهای قبلی مربوطه از طریق معیارهای معمولی (به عنوان مثال، تعداد ساعت ها، تعداد سلول ها و مساحت) و عملکرد هزینه QCA Specific [16] مقایسه می‌کنیم.

     بقیه این ارائه به شرح زیر برگزار می شود. بخش‌های II و III به ترتیب مختصراً مقدمه ای کلی برای QCA و کارهای قبلی مربوط به جمع کننده‌های QFA و QCA را به ترتیب ارائه می دهد. جزئیات مربوط به متقاطع استفاده شده ، طرح QFA پیشنهادی و جمع کننده مربوط به جریان حمل و نقل مربوطه در بخش IV ارائه شده است. در بخش V ، عملکرد QFA ها و جمع کننده بیت متناظر را با دو معیار متفاوتی معمولی و QCA خاص مقایسه می‌کنیم. سرانجام در بخش ششم نتیجه گیری می‌کنیم.

2.QCA به طور خلاصه

     سلول اولیه در فناوری QCA ، همان‌طور که در شکل 1 (a) نشان داده‌شده است، حاوی چهار نگهدارنده محل الکترون یا نقاط کوانتومی است. به طور معمول دو الکترون به داخل سلول تزریق می‌شوند، جایی که در دو انتهای یکی از قطرهای سلول حاوی مربع دو نقطه قرار می گیرند. جايگاه هاي ديگر (يعني در امتداد لبه ها) امكان پذير نيست زيرا اين دو الكترون تمايل به دفع يكديگر دارند. بنابراین، دو قطب امکان پذیر است. عبارت شبیه به اسلش (/) نشانگر عبارت دودویی 1 است (شکل 1 (b)) را ببینید، و عبارت بَک اسلش (\) نشانگر عبارت دودویی صفر است (به شکل 1 (c) مراجعه کنید). قرار دادن دو سلول از این سلول در کنار یکدیگر به دلیل قانون دافعه کولومب ممکن است // (قسمت راست سمت شکل 2 (a)) یا \\ (قسمت پایین سمت چپ شکل 2 (a) را ببینید. با این وجود، قرار دادن دو سلول به گونه ای که آن‌ها فقط از یک گوشه نزدیک شوند منجر به سوئیچ قطبیت از / به \ یا برعکس می شود (به دو سلول میانی در شکل 2 (a) مراجعه کنید).

 A.گیت های QCA

ساختار QCA دارای دو گیت اصلی است:

1)     اینورتر QCA (QI): یک جفت سلول متعامد / و \ ، به عنوان دو سلول میانی در شکل 2 (a) ، به عنوان یک اینورتر QCA عمل می‌کنند. توجه داشته باشید که سلول‎های بالا و پایین صرفاً برای ورودی و خروجی هستند. برای مثال ، ورودی "1" در شکل 2 (a) معکوس شده است. از آنجا که احتمال شکست هر سلول QCA وجود دارد، یک اینورتر قوی تر از مسیری دو برابر مانند شکل 2 (b) [17] طراحی شده است.

2)     گیت QCA Majority (QM): یکی دیگر از گیت های اصلی مهم QCA، تابع Majority سه ورودی است. این گیت از پنج سلول QCA با ساختار متقاطع تشکیل شده است (شکل 3 را ببینید). قطبیت سلول مرکزی، همان‌طور که به عنوان سلول دستگاه شناخته می شود، از طریق دافع کولومب، با اکثر قطب های سه سلول ورودی برابر است. قطبی بودن سلول دستگاه به سلول خروجی منتقل می شود. به عنوان مثال، شکل 3 (a) و 3 (b) به ترتیب دو دروازه QM را با دو ورودی "1" و دو ورودی "0" به تصویر می کشند. علاوه بر این، یک دروازه QM با یک ورودی ثابت بر روی "0" یا "1" به ترتیب به عنوان یک دروازه AND یا OR عمل می کند. بنابراین، ترکیب اینورتر QM و QCA مجموعه منطقی  ی را ایجاد می کند.

Abstract

We use a coplanar QCA crossover architecture in the design of QCA full adders that leads to reduction of QCA cell count and area consumption without any latency penalty. This crossover uses non-adjacent clock zones for the two crossing wires. We further investigate the impact of these gains on carry flow QCA adders. These designs have been realized with QCADesigner, evaluated, and tested for correctness. For better performance comparison with previous relevant works, we use a QCA-specific cost function, as well as the conventional evaluation method. We show 23% cell count and 48% area improvements over the best previous QCA full adder design. Similar results for 4-, 8-, 16-, 32-, and 64-bit adders are 29% (22%), 24% (51%), 19% (54%), 13% (69%), and 9% (49%) cell count reduction (less area consumption), respectively.

I. INTRODUCTION

     As the nanometer scale CMOS devices are facing new realization challenges (e.g., increased leakage current leading to considerable static power dissipation) [1] new technologies are emerging as possible replacements for CMOS. Quantum-dot cellular automata (QCA) [2] represent one of such innovative platforms. The basic QCA cell, that is capable of representing a logical bit, occupies nano-scale area. A primitive QCA cell commonly contains two electrons, whose two possible coulomb repulsion [2] placements represent “1” and “0”.

     QCA realization of the full adder (FA), as the most commonly used digital arithmetic cell, has been the subject of considerably many research papers (e.g., [3][4][5][6][7]). To show the impact of such very fast and low power arithmetic cell, word wide QCA adders [3][5][6][8] and multipliers [6][9] have been designed. One problem with designing QCA composite cells and circuits is how to efficiently design the crossover wires to reduce costs (i.e., both QCA cell count and implementation complexity). Multi-layer solution bears high cost due to, for instance, fabrication issue [10]. Nor is favorable the Logical crossing [11], due to its high area overhead. However, to achieve coplanar crossover wiring, 45- degree rotated QCA cells have been proposed [4].

     This has its own problems, such as low robustness [12] and implementation cost overhead, due to coexistence of two types of QCA cells [10]. Nevertheless, another coplanar QCA crossover wires design takes advantage of time-division multiplexing that is supported by special 8-phase clocking scheme with three types of clocking signals [13]. This single type cell alternative is highly robust and easy to design. However, a recent technique [14], [15] that also uses single type cells, takes advantage of non-adjacent zones of a 4-phase clocking scheme to resolve the wire crossing in one layer.

     In this paper, we utilize the latter crossover technique in designing our QCA full adder (QFA) and the corresponding carry flow [6] adders. We compare our performance figures with those of relevant previous works via conventional metrics (i.e., number of clocks, cell count and area) and the QCAspecific cost function of [16].

     The rest of this presentation is organized as follows. Sections II, and III briefly cover a general introduction to QCA and the previous relevant works on QFA and QCA adders, respectively. Details of the used crossover, the proposed QFA design and the corresponding carry flow adders are offered in Section IV. In Section V, we compare the performance of QFAs and the corresponding ??-bit adders with two different conventional and QCA-specific metrics. Finally we conclude in Section VI.

II. QCA IN BRIEF

     The primitive cell in QCA technology, as depicted in Fig. 1(a), contains four electron place holders or quantum dots. Normally two electrons are injected into the cell, where they occupy two dots on the two ends of one of the diagonals of the containing square cell. Other placements (i.e., along the edges) are not possible since the two electrons tend to repulse one another. Therefore, two polarities are possible. The slash like polarity (/) represents binary 1 (see Fig. 1(b)), and the backslash (\) one represents binary 0 (see Fig. 1(c)). Placing two of such cells next to each other would form // (see righttop part of Fig. 2(a)) or \\ (see left-bottom part of Fig. 2(a)) compositions due to coulomb repulsion. However, placement of two cells such that they approach via only one corner leads to polarity switch from / to \ composition or vice versa (see the two middle cells in Fig. 2(a)).

A. QCA gates

There are two primary QCA gates:

     1) QCA Inverter (QI): A pair of orthogonal / and \ cells, as the two middle cells in Fig. 2(a), works as a QCA inverter. Note that the top and bottom cells are merely for input and output. For example, an input “1” is shown to be inverted in Fig. 2(a). Since there is a probability for each QCA cell to fail, a more robust double path inverter has been designed as in Fig. 2(b) [17].

     2) QCA majority (QM) gate: Another more important primary QCA gate realizes the 3-input majority function. This gate is composed of five QCA cells with a crossshape structure (see Fig. 3). Polarity of the central cell, as known as device cell, is enforced, via the coulomb repulsion, to be equal to the majority of polarities of three input cells. The device cell’s polarity is transferred to the output cell. For example, Figs. 3(a) and 3(b) depict two QM gates with two “1” and two “0” inputs, respectively. Moreover, A QM gate with one input fixed to “0” or “1” acts as an AND or OR gate, respectively. Therefore, the combination of QM and QCA inverter make a complete logic set.

چکیده

1. مقدمه

2. QCA به طور خلاصه

A. گیت‏ های QCA

B. سیم انتقال QCA

C. تقاطع

D. فناوری‏ های ساخت QCA

3. کارهای پیشین

A. تمام جمع ‏کننده QCA

B. آدرس n بیتی QCA

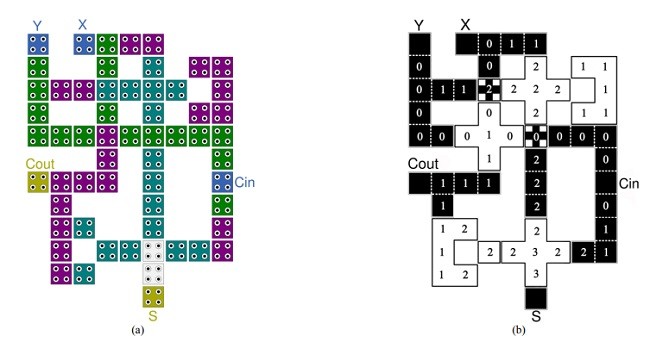
4. جمع‏ کننده جدید QFA و QCA

A. جزئیات طرح QX مبتنی بر Clock-zone

B. تأثیر QX مبتنی بر clock-zone در سایر روش‏ها

C. تمام جمع‏ کننده QCA

D. جمع ‏کننده –nبیتی ripple carry QCA

5. ارزیابی کارایی و مقایسه

6. نتیجه‏ گیری

Abstract

I.Introduction

II.QCA in Brief

A. QCA gates

B. QCA transmission wire

C. Crossover

D. QCA fabrication technologies

III.Related Works

A. QCA full adders

B. QCA ??-bit adders

IV.The New QFA and QCA Ripple Carry Adder

A. Details of clock-zone based QX design

B. The impact of clock-zone based QX in other technologies

C. The new QCA full adder

D. The new ??-bit ripple carry QCA adder

V.Performance Evaluation and Comparisons

VI.Conclusion