دانلود رایگان مقاله تجمیع برنامه نویسی شبکه ی ژنتیک و مسئله ی کوله پشتی

چکیده

         این تحقیق شمال پیاده سازیِ برنامه نویسی شبکه ی ژنتیک (GNP) و برنامه نویسی پویای استاندارد به منظور حل مسئله ی کوله پشتی (KP) به عنوان سیستم پشتیبانی تصمیم برای خوشه بندی رکورد در پایگاه های داده ی توزیع شده می شود. تخصیص قطعه با مسئله ی محدودیت ظرفیت انباره، پیش زمینه ای برای روش پیشنهاد شده است. مسئله ی ظرفیت انباره برای توزیع مجموعه ها در چندین سایت (خوشه) است. مقدار کل قطعه ها در هر سایت نباید از ظرفیت سایت تجاوز کند، در حالیکه روند توزیع باید رابطه (تشابه) ی بین قطعه ها در هر سایت را حفظ کند. هدف، توزیع داده ی بزرگ بوسیله ی لحاظ کردن شباهتِ داده ی توزیع شده در هر سایت، در سایتهای مشخصی با مقدار محدود ظرفیت است. GNP برای حل این مسئله به کار گرفته می شود تا قواعد را بوسیله ی لحاظ کردن مشخصاتِ (محدوده ی مقدار) هر ویژگی در یک مجموعه ی داده، استخراج کند. روش پیشنهاد شده، روش استخراج قاعده ی انتخاب تصادفی جزیی در GNP را ارائه می کند تا الگوهای متداول در یک پایگاه داده را برای بهبود الگوریتم خوشه بندی (خصوصا برای مسائل داده ی بزرگ) شناسایی کند. مفهوم KP برای مسئله ی ظرفیت انباره به کار گرفته می شود و برنامه نویسی پویای استاندارد بوسیله ی لحاظ کردن شباهت (مقدار) و مقدار داده (وزن) ی متناسب با هر قاعده برای قواعد توزیع استفاده می شود تا ظرفیت های سایت را تطبیق دهد. از نتایج شبیه سازی مشخص می شود که روش پیشنهاد شده، برتری هایی نسبت به الگوریتم های خوشه بندی مرسوم نشان می دهد و از این رو روش پیشنهاد شده، روش خوشه بندی جدیدی با مسئله ی ظرفیت انباره ی اضافی فراهم می کند.

1. دیباچه

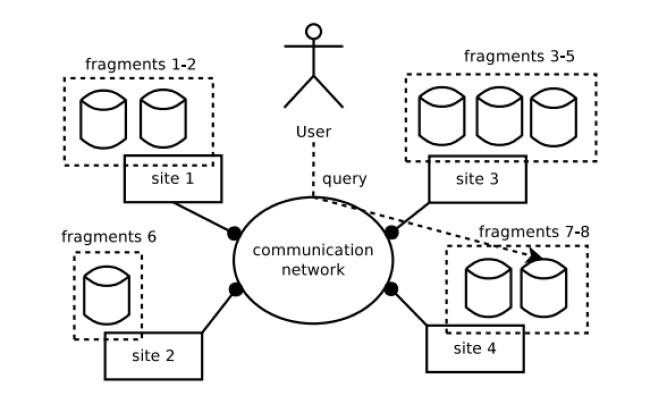
         سیستم مدیریت پایگاه داده ی توزیع شده (DDBMS) می تواند راه حلی برای سیستم های اطلاعاتیِ مقیاس بزرگ با مقادیر بزرگِ رشد داده و دسترسی داده باشد. پایگاه های داده ی توزیع شده (DDB) مجموعه ای از داده است که به طور منطقی متعلق به همان سیستم می باشد اما در سراسر سایت های شبکه ی کامپیوتر (شکل 1) پخش شده است. پس از آن DDBMS به عنوان یک سیستم نرم افزاری تعریف می شود که امکان مدیریت DDB را فراهم می کند و توزیع داده بین پایگاه های داده و نرم افزار را برای کاربران شفاف می کند. 

         روش های دسترسی کارآمد و تکنیک های ذخیره ی داده به طور فزاینده ای برای مدیریتِ تکثیر داده، در جهت قابل قبول نگه داشتن زمان پاسخِ جست و جو مهم شده اند. یک راه برای بهبود زمان پاسخ جست و جو، کاهش دادنِ تعداد I/O های دسیک از طریق خوشه بندی عمودی (خوشه بندی ویژگی) و/یا افقی (خوشه بندی رکورد) پایگاه داده است. بهبود در زمان بازیابیِ رکورد های چند ویژگی می تواند بدست آید اگر ثیت های مشابه در فضای فایل به صورت نتیجه ی بازسازی نزدیک به هم گره بندی شده باشند. این موضوع به خاطر این است که هر چقدر احتمال مقیم شدنِ دو هدف یا بیشتر در همان صفحه ی انباره کاهش پیدا کند، انتقال های صفحه ی کمتری مورد نیاز می باشد.

           در این مقاله، یک روش جدیدکه برنامه نویسی شبکه ی ژنتیک و برنامه نویسی پویای استاندارد را برای خوشه بندی رکورد تجمیع می نماید تا مسائل کوله پشتی (KP) را حل کند، ارائه می شود. فرضیه ی این تحقیق این است که پیاده سازیِ GNP برای داده کاوی می تواند خوشه های کارآمدی از مجموعه های داده ی پیچیده شده ایجاد کند و مفهوم KP می تواند با لحاظ کردن مقدار (شباهت داده) و جرم (اندازه ی داده) در DDBMS  برای تعریف مسئله ی توزیع قطعات در سایت های متعدد استعمال شود. بنابراین، این روش می تواند راه حلی برای تخصیص قطعه و مسائل ظرفیت انباره ی سایت باشد.

         این مقاله به صورت پیش رو سازمان دهی شده است: بخش 2 بررسی اجمالی از چارچوب پیشنهاد شده را تشریح می کند، بخش 3 مروری از ادبیات علمی ارائه می کند، بخش 4 الگوریتمِ دقیقِ چارچوب پیشنهاد شده را نشان می دهد، بخش 5 نتایج شبیه سازی را نشان می دهد و در نهایت بخش 6 به نتیجه گیری تخصیص داده شده است.

2. بررسیِ چارچوب پیشنهاد شده

2.1. برنامه نویسی شبکه ی ژنتیک

         GNP یک تکنیک بهینه سازی تکاملی است که به جای رشته ها در الگوریتم ژنتیک یا درخت ها در برنامه نویسی ژنتیک از ساختارهای گراف مستقیم شده استفاده می کند. این کار منجر به تقویت توانایی ارائه با برنامه های فشرده می شود که از استفاده ی مجددِ گره ها در ساختار گراف استنتاج شده اند.

        گره ها در GNP به عنوان واحد های کمینه ی داوری و عمل تفسیر می شوند. و انتقال گره، قواعد برنامه را ارائه می کند. GNP بعد از آغاز انتقال گره از گره شروع، در زمانی که فعالیت ها کامل شود به گره شروع باز نمی گردد. داوری و عمل بعدی همیشه تحت تاثیرِ انتقال گره قبلی می باشد. داوری و پردازشِ برنامه های GNP در سطح گره اجرا می شوند.

        ساختار پایه ی GNP در شکل 2 نشان داده می شود که S گره شروع را معنی می دهد. دو نوع دیگر گره، گره های داور و گره های پردازش، به ترتیب توابع داوری Jp و پردازش Pq را دارند. Jp ، p امین تابع داوریِ ذخیره شده در کتابخانه برای گره های داوری را نشان می دهد در حالی که  ، q امین تابع پردازش ذخیره شده در یک کتابخانه برای گره های پردازش را نشان می دهد.

        GNP در این مقاله، از طریق تحلیل رکورد ها برای اداره کردنِ قواعد استخراج از مجموعه های داده استفاده می شود. هر گره داوری یک ویژگی با محدوده ی مقدار را ارائه می کند. برای مثال، ویژگی قیمت می تواند به سه محدوده (پایین، وسط، بالا) تقسیم شود و یک محدوده به یک گره داوری تخصیص داده می شود. GNP قواعد را از طریق تکامل دادن تجمیع گره ها ایجاد می کند و پوشش قواعد استخراج شده را اندازه گیری می کند. پوشش بدین معنا است که هر قاعده چه میزان رکورد در یک مجموعه ی داده می تواند ارائه کند (پوشش). قواعدی که حداقل یک رکورد را پوشش می دهند، در مخزن قواعد ذخیره خواهند شد و بعد از آن قواعد ذخیره شده به منظور کاربردی برای فاز KP، در چندین سایت توزیع می شوند. هدف این مقاله توزیع قواعد است نه داده که با لحاظ کردنی تشابهات بین قواعد و داده در توزیع هر گونه داده در سایت ها مشارکت می کند. توضیحِ پیاده سازی GNP در استخراج قاعدهف به تفصیل در بخش 4.1 قابل دسترس خواهد بود.

Abstract

        This research involves implementation of genetic network programming (GNP) and standard dynamic programming to solve the knapsack problem (KP) as a decision support system for record clustering in distributed databases. Fragment allocation with storage capacity limitation problem is a background of the proposed method. The problem of storage capacity is to distribute sets of fragments into several sites (clusters). Total amount of fragments in each site must not exceed the capacity of site, while the distribution process must keep the relation (similarity) between fragments within each site. The objective is to distribute big data to certain sites with the limited amount of capacities by considering the similarity of distributed data in each site. To solve this problem, GNP is used to extract rules from big data by considering characteristics (value ranges) of each attribute in a dataset. The proposed method also provides partial random rule extraction method in GNP to discover frequent patterns in a database for improving the clustering algorithm, especially for large data problems. The concept of KP is applied to the storage capacity problem and standard dynamic programming is used to distribute rules to each site by considering similarity (value) and data amount (weight) related to each rule to match the site capacities. From the simulation results, it is clarified that the proposed method shows some advantages over the conventional clustering algorithms, therefore, the proposed method provides a new clustering method with an additional storage capacity problem.

1 Introduction

        Distributed database management system (DDBMS) could be a solution for large scale information systems with large amount of data growth and data accesses. A distributed database (DDB) is a collection of data that logically belongs to the same system but is spread over the sites of a computer network (Fig. 1). A DDBMS is then defined as a software system that permits the management of DDB and makes the distribution of data between databases and software transparent to the users (Bhuyar, Gawande, & Deshmukh, 2012; Zilio et al., 2004).

        To handle the data proliferation, efficient access methods and data storage techniques have become increasingly critical to maintain an acceptable query response time. One way to improve query response time is to reduce the number of disk I/Os by clustering the database vertically (attribute clustering) and/or horizontally (record clustering) (Guinepain & Gruenwald, 2006, 2008). Improvements in the retrieval time of multi-attribute records can be attained if similar records are grouped close together in the file space as a result of restructuring. This is because fewer page transfers are required as the probability of two or more of the target records residing in the same page of storage is increased (Lowden & Kitsopanidis, 1993).

        In this paper, a novel method combining genetic network programming (GNP) (Mabu, Chen, Lu, Shimada, & Hirasawa, 2011; Shimada, Hirasawa, & Hu, 2006) and standard dynamic programming solving knapsack problems (KP) (Singh, 2011; Lai, 2006) for record clustering is proposed. Hypothesis of this research are the implementation of GNP for data mining can create effective clusters from complicated datasets and the concept of KP can be used to define the problem of distributing fragments to several sites considering value (similarity of data) and mass (data size) in DDBMS. Therefore, it could be a solution to the fragment allocation and site storage capacity problems.

       This paper is organized as follows. Section 2 describes the review of the proposed framework, Section 3 describes a review of literatures, 4 describes the detailed algorithm of the proposed framework, section 5 shows the simulation results, and finally section 6 is devoted to conclusions.

2 Review of the Proposed Framework

2.1 Genetic Network Programming

      GNP is an evolutionary optimization technique, which uses directed graph structures instead of strings in genetic algorithm (Holland, 1975) or trees in genetic programming (Koza, 1992), which leads to enhancing the representation ability with compact programs derived from the re-usability of nodes in a graph structure.

       In GNP, nodes are interpreted as the minimum units of judgement and action, and node transition represents rules of the program. After starting the node transition from the start node, GNP does not return to the start node when the actions are completed. The next judgement and action are always influenced by the previous node transition. Judgement and processing of GNP programs are performed on the node level.

       The basic structure of GNP is illustrated in Fig. 2, with S denoting the start node. Two other kinds of nodes, judgement nodes and processing nodes, have judgement function Jp and processing function Pq, respectively. Jp (p = 1, . . . , n) denotes the p-th judgement function stored in a library for judgement nodes, while Pq (q = 1, . . . , m) denotes the q-th processing function stored in a library for processing nodes (Mabu et al., 2011; Shimada et al., 2006).

       In this research, GNP is used to handle rule extraction from datasets by analyzing the records. Each judgment node represents an attribute with value range. For example, price attribute could be divided into three ranges (low, middle, high), and one range is assigned to one judgment node. GNP makes rules by evolving combinations of nodes and measures the coverage of the extracted rules. Coverage means that how much records in a dataset each rule can represent (cover). Rules that cover at least one record will be stored in the rule pool, then in the application for KP phase, the stored rules are distributed to several sites. The point of this paper is to distribute rules, not the data, which contributes to distributing any data into the sites considering the similarities between rules and data. The detailed explanation of the implementation of GNP in rule extraction is available in section 4.1.

چکیده

1. دیباچه

2. بررسیِ چارچوب پیشنهاد شده

2.1. برنامه نویسی شبکه ی ژنتیک

2.2. مسئله ی کوله پشتی

3. برررسی ادبیات علمی

4. تجمیع مسئله ی کوله پشتی و GNP

4.1. استخراج قاعده ی GNP

4.1.1. تعریف گره

4.1.2. ترتیب گره: انتخاب تصادفی کامل

4.1.3.  ترتیب گره: انتخاب تصادفی جزیی

4.2. توزیع قاعده بر مبنای برنامه نویسی پویای استاندارد برای حل کردن مسئله ی کوله پشتی

4.3. تحلیل پیچیدگی

5. شبیه سازی ها

5.1. استخراج قاعده ی GNP

5.1.1. تحلیل پاراکترِ نرخ همگذری و نرخ دگرگونی

5.1.2. مقایسه ی روش های ترتیب گره

5.2. توزیع قاعده ی کوله پشتی

5.3. مقایسه با دیگر روش ها

6. نتیجه گیری

منابع

Abstract

1 Introduction

2 Review of the Proposed Framework

2.1 Genetic Network Programming

2.2 Knapsack Problem

3 Literature review

4 Combination of GNP and Knapsack problem

4.1 GNP Rule Extraction

4.1.1 Node Definition

4.1.2 Node Arrangement : Full Random

4.1.3 Node Arrangement : Partial Random

4.2 Rule Distribution based on standard dynamic programming for solving Knapsack Problem

4.3 Complexity Analysis

5 Simulations

5.1 GNP Rule Extraction

5.1.1 Parameter Analysis of Crossover Rate and Mutation Rate

5.1.2 Comparison of Node Arrangement Methods

5.2 Knapsack Rule Distribution

5.3 Comparison with other methods

6 Conclusions

References