
دانلود رایگان مقاله ترکیبی از انتخاب هادی بهینه و مکان یابی خازن در سیستم های توزیع شعاعی
مقدمه
هدف اصلی سیستم توزیع الکتریکی (EDS) فراهم کردن خدمات معتبر و مقرون به صرفه برای مصرف کنندگان با توجه به کیفیت قدرت در محدوده ی استاندارد می باشد. بنابراین، برنامه ریزی مناسب EDS و در نتیجه ارزیابی جنبه های مختلف مانند هزینه نصب تجهیزات جدید، میزان استفاده از تجهیزات و کیفیت خدمات، قابلیت اطمینان سیستم توزیع و کاهش تلفات با توجه به افزایش بارهای سیستم و بارهای تازه نصب شده برای افق های برنامه ریزی ضروری است (1). به حداقل رساندن تلفات در سیستم های توزیع، اخیرا اهمیت بیشتری جلب کرده است زیرا روند اتوماسیون توزیع نیازمند کارآمدترین سناریو عامل برای تغییرات کارایی اقتصادی خواهد بود. تلفات برق در سیستم های توزیع به حدود 78% از کل تلفات در سیستم های قدرت الکتریکی مربوط است (M. Mozaffari Legha, 2012).
مزایای افزودن خازن های موازی (شنت)، بهبود ضریب قدرت، مشخصات ولتاژ فیدر(سیم تغذیه)، کاهش خسارت برق و افزایش ظرفیت در دسترس فیدر(سیم تغذیه) می باشد. بنابراین، یافتن مکان بهینه و اندازه های خازن ها در سیستم برای رسیدن به اهداف ذکر شده ی فوق مهم می باشد. از آنجاییکه مکانیابی خازن بهینه یک مشکل بهینه سازی ترکیبی پیچیده است، تکنیک ها و الگوریتم های بهینه سازی متفاوتی در گذشته پیشنهاد شده است. (Baghzouz و Ertem 1990) این مفهوم را پیشنهاد کرده اند که اندازه ی کناره خازن به عنوان متغیر پیوسته در نظر گرفته می شد. H. Ng et al (2000) با استفاده از منطق تقریبی فازی، مشکل مکانیابی خازن را پیشنهاد کرد. (Ji Pyng Chiou et al 2006) الگوریتم تکامل متمایز متغییر مقیاس هیبرید را برای مکانیابی خازن در سیستم توزیع پیشنهاد کرد. با این وجود، تنها خسارت در خطوط در نظر گرفته شد و مقادیر تنها برای خسارت خطوط تعریف شد.
چندین پارامتر وجود دارد که باید برای مدل سازی مشکل انتخاب اندازه ی هادی (CSS) در نظر گرفته شود مانند: زندگی اقتصادی هادی، نرخ تنزیل، هزینه های کابل و نصب و نوع مدار ( رویی یا زیرین). رویکرد برنامه نویسی پویا برای حل مشکل CSS در (3) مورد استفاده قرار گرفت. آن ها مدل هایی برای نشان دادن هزینه سیم تغذیه (فیدر)، تلفات انرژی و تنظیم ولتاژ به عنوان تابع سطح مقطع هادی ارائه داده اند. در (Mahdi Mozaffari Legha et al 2013) انتخاب اندازه هادی با توجه به معیارهای مالی و مهندسی در سیم تغذیه (فیدر) انجام شده است. در (S. Sivanagaraju et al 2002) و (6) مشکل CSS با استفاده از روش های اکتشافی حل شده است.مرجع (S. Sivanagaraju et al, 2002) با استفاده از معیارهای اقتصادی به همراه انتخاب تکنیکی با استفاده از شاخص حساسیت از فاز انتخاب استفاده می کند که به دنبال اطمینان بخشیدن به عمل ممکن EDS می باشد، در حالیکه با استفاده از شاخص حساسیت جدید برای تزریق توان راکتیو یک روش اکتشافی را نشان می دهد. روش های اکتشافی قوی هستند، به راحتی به کار گرفته می شوند اما به طور معمول به راه حل بهینه محلی متمایل هستند. در (su. Ching et al, 2001)، یک مدل خطی عدد صحیح مختلط برای مشکل انتخاب اندازه هادی در سیستم های توزیع شعاعی ارائه شده است.
در این مقاله، ترکیبی هم از مکانیابی خازن و هم روش های انتخاب هادی توسعه یافته است تا خسارت شبکه توزیع را کاهش دهد. در این روش، تابع هدف مکان خازن و انتخاب هادی کاهش خسارت قدرت در حداقل هزینه و افزایش ولتاژ می باشد. محدودیت، محدوده ی ولتاژ می باشد که ظرفیت انرژی رایج هادی انتخاب شده را مجاز می سازد. برای حل این مشکل بهینه سازی، روش الگوریتم ژنتیک (GA) مورد استفاده قرار گرفته است. روش پیشنهادی بر سیستم شعاعی 69-bus با 3 نوع هادی در دسترس و 69 اندازه ی متفاوت خازن آزمایش شده است. نتایج نشان داد که تابع هدف پیشنهاد شده، خسارت سیستم را با در نظر گرفتن همه ی محدودیت ها و ترکیب خازن ها و انتخاب هادی به حداقل می رساند.
الگوریتم ژنتیک
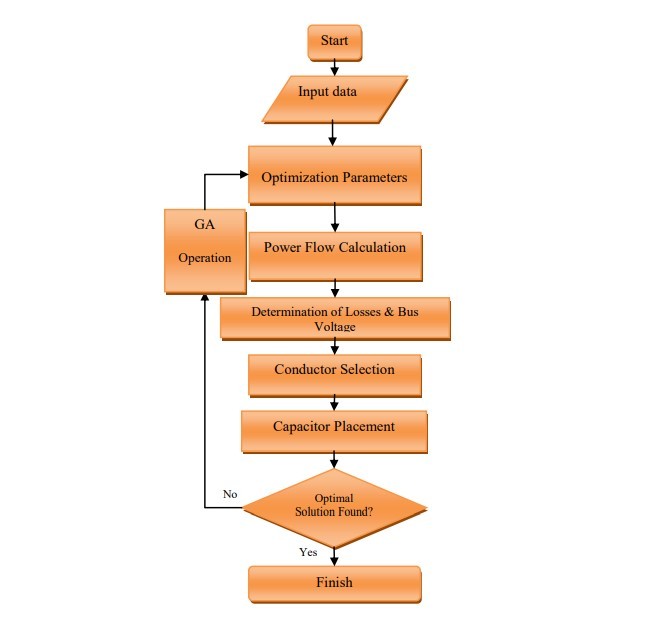
GA ها الگوریتم های جستجوی تعمیم داده شده هستند که بر مبنای مکانیک ژنتیک طبیعی می باشند (14).GA جمعیتی از افراد را حفظ می کند که نشان دهنده ی راه حل کاندید شده به مشکل ارائه شده است. هر فرد در جمعیت ارزیابی می شود تا مقیاسی به تناسب اش به مشکل از تابع هدف داده شود. GA راه حل ارزیابی را با اپراتورهای تصادفی یعنی انتخاب، تقاطع و جهش ترکیب می کند تا بهینگی را بدست آورد. نمودار جریان پیشنهادی GA در شکل 2 نشان داده شده است.
آزمایشات و نتایج
شبیه سازی با استفاده از رویکرد ICA در شبکه توزیع شعاعی 69-bus انجام شده است تا دقت و همینطور کارایی تکنیک راه حل ارائه شده را نشان دهد. نمودار خطی برای سیستم های توزیع شعاعی در شکل 3 نشان داده شده است. میزان بهای پایه سیستم به عنوان 20kV و 20 MVA در نظر گرفته شد. جزئیات هادی های توزیع در جدول 1 داده شده است. سیستم شامل 60 ترانسفورماتور با مقادیر متعدد است. جزئیات ترانسفورماتورهای توزیع در جدول 2 داده شده است.مجموع بار متصل بر سیستم 2550KVA است و اوج تقاضا برای سال 2120KVA در PF 0.8 می باشد (Mahdi Mozaffari Legha, 2011).
ABSTRACT
In This paper presents an approach for optimal placement and sizing of fixed capacitor banks and also optimal conductor selection in radial distribution networks for the purpose of economic minimization of loss and enhancement of voltage profile. The objective function includes the cost of power losses, capacitors and conductors. Constraints include voltage limit, maximum permissible carrying current of conductors, size of available capacitors and type of conductors. The optimization problem is solved by the genetic algorithm method and the size and the type of the capacitors and conductors is determined. By applying the proposed method, the economic costs and power losses are reduced to a considerable degree while enhancing the voltage profile. To demonstrate the validity of the proposed algorithm, computer simulations are carried out on actual power network of Kerman Province, Iran and the simulation results are presented and discussed.
INTRODUCTION
The main objective of an electrical distribution system (EDS) is providing a reliable and cost-effective service to consumers with considering power quality within standard ranges. Thus, it is necessary to properly plan the EDS and thus evaluate several aspects such as, new equipment installation cost, equipment utilization rate, and quality of service, reliability of the distribution system and loss minimization, considering an increase of system loads, and newly installed loads for the planning horizon [1]. The loss minimization in distribution systems has assumed greater significance recently since the trend towards distribution automation will require the most efficient operating scenario for economic viability variations. The power losses in distribution systems correspond to about 78% of total losses in electric power systems (M. Mozaffari Legha, 2012).
The advantages with the addition of shunt capacitors banks are to improve the power factor, feeder voltage profile, Power loss reduction and increases available capacity of feeders. Therefore it is important to find optimal location and sizes of capacitors in the system to achieve the above mentioned objectives. Since, the optimal capacitor placement is a complicated combinatorial optimization problem, many different optimization techniques and algorithms have been proposed in the past. (Baghzouz and Ertem, 1990) proposed the concept that the size of capacitor banks was considered as a continuous variable. H. Ng et al (2000) proposed the capacitor placement problem by using fuzzy approximate reasoning. (Ji Pyng Chiou et al, 2006) proposed the variable scale hybrid differential evolution algorithm for the capacitor placement in distribution system. However, considered only the losses in the lines and the quantification were defined for the line losses only.
There are several parameters to be taken into account to model the conductor size selection (CSS) problems such as: conductor’s economic life, discount rate, cable and installation costs and type of circuit (overhead or underground). Dynamic programming approach was utilized to solve the CSS problem in [3]. They presents models to represent feeder cost, energy loss and voltage regulation as a function of a conductor cross-section. In (Mahdi Mozaffari Legha et al, 2013), the conductor size selection performed with consideration of financial and engineering criteria in the feeder. In (S. Sivanagaraju et al, 2002) and [6] the CSS problem is solve using heuristic methods. Reference (S. Sivanagaraju et al, 2002) uses a selection phase by means of economic criteria, followed by a technical selection using a sensitivity index that seeks to ensure a feasible operation of the EDS, whereas presents a heuristic method using a novel sensitivity index for the reactive power injections. The heuristic methods are robust, easily applied; however, they normally converge to a local optimum solution. In (Su. Ching et al, 2001), a mixed integer linear model for the problem of conductor selection size in radial distribution systems is presented.
In this paper, a combination of both capacitor placement and conductor selection methods is developed to reduce the loss of a distribution network. In this method the objective function of capacitor placement and conductor selection is to reduce the power loss within minimum costs and enhancing the voltage profile. The constraints are voltage limits, allowable current energy capacity of selected conductors. To solve this optimization problem, Genetic Algorithm (GA) method is used. The proposed method is tested on a 69-bus radial system with 3-type of available conductors and 69 different sizes of capacitors. The results show that proposed objective function minimizes the loss of the system by considering all of the constraints and incorporating capacitors and conductor's selection.
POWER FLOW ANALYSIS METHOD
Power flow evaluation includes the calculation of bus voltages and line flows of a network. A singlephase representation is adequate because power systems are usually balanced. Associated with each bus, there are four quantities to be determined or specified: the real and reactive powers, the voltage magnitude and phase angle. Fig 1 shows an m-bus radial distribution system wherein bus i has a load and a shunt capacitor (Su. Ching Tzong et al, 2001).
Objective Function
In each optimization problem, objective function should be defined. Eq. (11) illustrates the proposed objective function in this paper. This objective function aims at minimizing the total annual cost due to capacitor placement, conductor selection and power losses with constraints that include limits on voltage Eq. (13), maximum permissible carrying current of conductors Eq. (14), size of installed capacitors and type of selected conductors. These constraints are added as penalty functions to the objective function.
Genetic Algorithm
G ’s are generalized search algorithms based on the mechanics of natural genetics [ ] G maintains a population of individuals that represent the candidate solutions to the given problem. Each individual in the population is evaluated to give some measure to its fitness to the problem from the ob ective function G ’s combine solution evaluation with stochastic operators namely, selection, crossover and mutation to obtain optimality. The flow chart of proposed GA is depicted in Fig. 2.
مقدمه
الگوریتم ژنتیک
آزمایشات و نتایج
نتیجه گیری
منابع
INTRODUCTION
Genetic Algorithm
TESTS AND RESULTS
CONCLUSION
REFERENCES
