دانلود رایگان مقاله استفاده از امکان‌ سنجی معیار منطق برای کاهش اندازه تست با تضمین تشخیص نقص

چکیده

             برخی از معیارهای پوشش تست منطق نرم‌افزار نیازمند ورودی‌هایی  هستند که تضمین‌کننده تشخیص مجموعه‌ بزرگی از انواع نقص‌ها دارند. یکی از معیارهای قدرتمند در این زمینه، MUMCUT است که از سه معیار تشکیل شده است که در آن هر مولفه تشخیص نوع خاصی از نقایص را تضمین می‌کند. در عمل، معیارها ممکن است با توجه به نوع نقصی که تشخیص داده شده است با یکدیگر همپوشانی داشته باشند در نتیجه این موضوع منجر به آزمون‌های زائد متعددی خواهد شد، اما به دلیل این حقیقت ناخوشایند که نیازمندی‌های آزمون‌ غیرعملی در آزمون‌ها مشخص نمی‌شود، تمامی معیارهای سازنده مورد نیاز است. بینش کلیدی این مقاله در تجزیه و تحلیل امکان‌سنجی معیار تشکیل‌دهنده‌ای است که می‌تواند برای کاهش اندازه مجموعه آزمون بدون فداکردن تشخیص نقص مورد استفاده قرار بگیرد. به عبارت دیگر، معیارهای گران را می‌توان برای مواقعی رزرو کرد که استفاده از آن‌ها واقعا ضرروری باشد. در این مقاله یک معیار منطقی جدیدی با نام، کمینه  MUMCUT، بر اساس بینش مقاله معرفی شده است. با توجه به گزاره داده شده در کمینه DNF، تعیین می‌کند که کدام یک از معیارهای سازنده در سطح اصطلاحات و لیترال‌ها  منحصر‌به‌فرد امکان‌پذیر است. این موضوع به نوبه خود تعیین می‌کند که کدام معیارها مجددا در سطح اصطلاحات و لیترال‌ها منحصر‌به‌فرد ضروری هستند. در این مقاله یک مطالعه تجربی با استفاده از گزار‌ه‌ها در نرم‌افزار اویونیک ارائه شده است. این مطالعه نشان می‌دهد که کمینه MUMCUT سبب کاهش اندازه مجموعه آزمون تا حدی می‌شود که تنها چند درصد از انداره مجموعه آزمون در صورتی که امکان‌پذیری در نظر گرفته نشده باشد، مورد نیاز است و تشخیص نقص را نیز فدای این موضوع نمی‌کند.

1. مقدمه

          نیازمندی‌های  آزمون غیرممکن  تقاضاهایی برای آزمون‌ها هستند که به سادگی وجود ندارند. آن‌ها حقایقی ناخوشایند از زندگی در آزمون نرم‌افزار هستند. آن‌ها مهندسان آزمون را گیج می‌کنند، مهندسان آزمون باید تصمیم بگیرند که آیا نیازمندی آزمونی معین واقعا غیرممکن است یا اگر یک چستجوی دقیق‌تر برای ورودی مناسب در سفارش است. آن‌ها همچنین تلاش‌های محققان برای ارتباط معیارهای پوشش را نیز به سردرگمی می‌کشانند. پس بر اساس تعریف، نیازمندی آزمون غیرممکن برای یک معیار معین، نتیجه آزمون را نمی‌دهد. اگر وقوع نیازمندی آزمون متناظر برای یک معیار «ضعیف‌تر» ممکن باشد، امکان‌ناپذیری می‌تواند معیار ظاهرا «قوی‌تری» برای شکست در گنجاندن «ضعیف‌تر» باشد. بسیاری از موارد معروف از این پدیده در پیشینه تحقیق انجام آزمون یافت می‌شود. در این مقاله، ما به امکان‌ناپذیری در زمینه معیارهای آزمون منطقی طراحی‌شده برای سلسله‌مراتب  نقض لاو  و یو  خواهیم پرداخت [9]. 

            ما آزمون گزاره‌ها را بر روی متغیرهای بولین در انزوا  در نظر می‌گیریم. در این دامنه محدود، تعیین اینکه آیا نیازمندی آزمون امکان‌پذیر است امری ساده خواهد بود. البته، هنگامی که این گزاره‌ها در داخل برنامه‌های واقعی دفن می‌شوند، همچنان یک مسئله قابل‌کنترل دشوار در انتخاب ورودی‌ها برای هدایت متغیرها در گزاره‌ها به مقادیر مطلوب وجود دارد اما این موضوع تمرکز این تحقیق نیست.

           یک گزاره در متغیرهای n حداکثر دارای 2 n آزمون است. برای برنامه‌های کاربردی که در آن‌ها n بزرگ است، مجموعه آزمون جامع اغلب بسیار گران‌قیمت است. از این رو، برخی از معیارهای منطقی قابلیت تشخیص نقص را برای کاهش اندازه مجموعه آزمون فدا می‌کنند. در این مقاله امکان‌سنجی برای بهبود راه‌حل‌های این تبادل مورد تجزیه و تحلیل قرار می‌گیرد. ما بر روی سه نقص تمرکز خواهیم کرد: نقص درج لیترال  (LIF)، نقص مرجع لیترال  (LRF) و نقص ازقلم‌افتادگی لیترال [8] اسامی این سه مورد هستند. یک LIF شامل درج یک لیترال یا یک لیترال منفی در داخل یک اصطلاح است. یک LRF مستلزم جایگزینی یک لیترال یا یک لیترال منفی از یک اصطلاح دیگر است. یک LOF مستلزم حذف یک لیترال است. LIF، LRF و LOF به دو دلیل مهم هستند. نخست، آن‌ها اشتباهات برنامه‌نویس را تقلید می‌کنند. فرضیه برنامه‌نویس شایسته [1] بیان می‌کند که برنامه‌نویس شایسته برنامه‌هایی را می‌نویسد که از نسخه فعلی با تعداد نسبتا کمی از نقص‌های نمونه تفاوت دارد و بنابراین نقص‌های سلسله مراتبی خطاهای محتملی هستند که باید مورد آزمون قرار بگیرند. دوم سلسله مراتب نقص لاو و یو [6] اطمینان می‌دهد که  تشخیص این نقص‌ها سبب شناسایی سایر نقص‌ها خواهد شد. یعنی این سه خطا در بالای یک سلسله‌مراتبی از نقص‌ها قرار دارند.

          چن ، لاو و یو [4] معیار پوشش MUMCUT را توسعه‌ دادند که به طور خاص برای تضمین شناسایی تمامی نقص‌ها در سلسله مراتب نقص‌ها کاربرد دارد. معیار MUMCUT مشتمل بر سه معیار مولفه اصلی است که عبارتند از: چند نقطه درست منحصر‌به‌فرد (MUTP)، چند نقطه غلط نزدیک (MNFP) و نقطه درست منحصر‌به‌فرد متناظر با نقطه غلظ نزدیک (CUTPNFP). جزئیات این معیارهای سازنده در بخش 2 ارائه شده است. برای این مقاله، مسئله کلیدی نقش امکان‌سنجی در هر معیار مولفه ضروری است. 

          به طورخاص اگر MUTP امکان‌پذیر باشد، می‌توان آن را با آزمون‌های کمتری نسبت به آنچه که CUTPNFP یا MNFP نیاز دارد، تقویت کرد و در عین حال کل سلسله مراتب نقص‌ها را شناسایی کرد. در صورتی که MUTP غیرممکن باشد، شرایط پیچیده خواهد شد. زمانی که MUTP غیرممکن است ولی CUTPNFP امکان‌پذیر است، اصلا نیازی به MNFP  نیست. اگر هم MUTP و هم CUTPNFP غیرممکن باشند، پس MNFP مورد نیاز است. یک جنبه کلیدی این مقاله این است که استدلال‌های غیرممکن در سطح ریزساختار اصطلاحات و لیترال‌ها اعمال می‌شود و بنابراین CUTPNFP و در صورت لزوم MNFP می‌تواند تنها در جایی که ضروری است مورد استفاده قرار بگیرد.

         MUMCUT رویکرد ساده‌ای دارد که نیاز به تمام سه معیار مولفه اصلی دارد. این رویکرد قطعا کارآیی لازم را دارد ولی گران است. CUTPNFP و به ویژه MNFP نیاز به تعداد زیادی از آزمون‌ها دارد اما همانطور که در بالا اشاره شد، تنها در موارد نسبتا کمی ضروری است.

           اعانه‌های این مقاله عبارتند از:

1) استفاده از تجزیه و تحلیل امکان‌سنجی معیار مولفه اصلی MUMCUT در سطح لیترال‌ها و اصطلاحات، این تجزیه و تحلیل سبب می‌شود که اندازه مجموعه آزمون بدون قربانی‌کردن تشخیص نقص کاهش پیدا می‌کند.

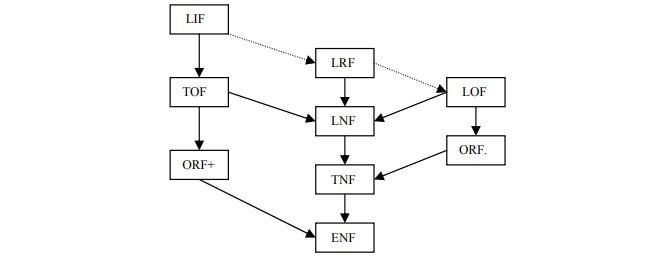
2) اصلاحی بر روابط تشخیص نقص سلسله‌مراتبی کار لاو و یو [9] بر اساس امکان‌سنجی معیار مولفه اصلی از معیار MUMCUT را انجام می‌دهد (شکل 1. 3).

3) یک معیار پوشش منطق جدیدی را ارائه می‌دهد که نام آن کمینه MUMCUT است و همچنین الگوریتمی برای تولید مجموعه آزمون‌های کمینه MUMCUT را ارائه می‌کند.

4) یک مطالعه موردی را نشان می‌دهد که در آن کاهش اندازه آزمون با کمینه MUMCUT امکان‌پذیر است.

           این مقاله بدین شرح مرتب شده است که باقی‌ بخش 1 به بررسی اصطلاحات منطق بولین و کارهای مرتبط در معیار منطق می‌پردازد. در بخش دوم، MUMCUT و سه معیار مولفه اصلی MNFP و CUTPNFP و MUTP مورد بررسی قرار خواهند گرفت. در بخش 3 سلسله‌مراتب نقص‌ها مورد بررسی خواهند گرفت. در بخش 4 نتایجی را توسعه خواهیم داد که تاثیر غیرممکن‌ بودن را در تشخیص‌ نقص ارائه می‌دهند و الگوریتمی را برای تعیین امکان‌سنجی هر کدام از معیارها در سطح اصطلاحات و لیترال‌ها نمایش خواهد داد و در نهایت این نتایج را به الگوریتم کمینه MUMCUT می‌افزاید. در بخش 5 یک مطالعه موردی به منظور ارزیابی کاهش اندازه مجموعه آزمون توسط کمینه MUMCUT ارائه شده است. در بخش 6 در مورد این موضوع بحث می‌کنیم که چگونه این کار مربوط به مسائل کلی‌تری از آزمون است و در بخش 7 به جمع‌بندی مقاله خواهیم پرداخت.

Abstract

          Some software testing logic coverage criteria demand inputs that guarantee detection of a large set of fault types. One powerful such criterion, MUMCUT, is composed of three criteria, where each constituent criterion ensures the detection of specific fault types. In practice, the criteria may overlap in terms of fault types detected, thereby leading to numerous redundant tests, but due to the unfortunate fact that infeasible test requirements don’t result in tests, all the constituent criteria are needed. The key insight of this paper is that analysis of the feasibility of the constituent criteria can be used to reduce test set size without sacrificing fault detection. In other words, expensive criteria can be reserved for use only when they are actually necessary. This paper introduces a new logic criterion, Minimal-MUMCUT, based on this insight. Given a predicate in minimal DNF, a determination is made of which constituent criteria are feasible at the level of individual literals and terms. This in turn determines which criteria are necessary, again at the level of individual literals and terms. This paper presents an empirical study using predicates in avionics software. The study found that Minimal-MUMCUT reduces test set size -- without sacrificing fault detection -- to as little as a few percent of the test set size needed if feasibility is not considered.

1. Introduction

         Infeasible test requirements are demands for tests that simply do not exist. They are an unfortunate fact of life in software testing. They confound test engineers, who must decide if a given test requirement really is infeasible or if a more diligent search for a suitable input is in order. They also confound attempts by researchers to relate coverage criteria. By definition, an infeasible test requirement for a given criterion does not result in a test. If the corresponding test requirement for a “weaker” criterion happens to be feasible, the infeasibility can cause an apparently “stronger” criterion to fail to subsume the “weaker” one. Many well known cases of this phenomenon pervade the testing literature. In this paper, we address infeasibility in the context of logic testing criteria designed for the fault hierarchy of Lau and Yu [9].

         We consider testing predicates over Boolean variables in isolation. In this finite domain, it is straightforward to determine whether a given test requirement is feasible. Of course, when these predicates are buried inside actual programs, there is still a difficult controllability problem of selecting inputs to drive the variables in the predicate to the desired values, but that is not the focus of this research.

        A predicate in n variables has at most 2n tests. For applications where n is large, the exhaustive test set is often prohibitively expensive. Hence, some logic criteria trade fault detection capability for reduced test set size. This paper analyzes feasibility to improve solutions to this tradeoff. We focus on three faults: the Literal Insertion Fault (LIF), the Literal Reference Fault (LRF), and the Literal Omission Fault [8]. A LIF involves inserting a literal, or the negation of a literal, into a term. A LRF involves replacing a literal with a literal, or the negation of a literal, from some other term. A LOF involves omitting a literal. The LIF, LRF, and LOF are important for two reasons. First, they mimic programmer mistakes. The competent programmer hypothesis [1] states that competent programmers often write programs that differ from a correct version by relatively few simple faults, and so faults in the hierarchy are plausible errors for which to test. Second, the fault hierarchy of Lau and Yu [9] assures that detection of these faults guarantees detection of other faults. That is, these three faults sit atop the fault hierarchy.

        Chen, Lau and Yu [4] developed the MUMCUT coverage criterion specifically to guarantee detection of all faults in the fault hierarchy. The MUMCUT criterion integrates three constituent criteria: the Multiple Unique True Point (MUTP), Multiple Near False Point (MNFP), and Corresponding Unique True Point Near False Point (CUTPNFP) criteria. Details of these constituent criteria are given in Section 2. For this paper, the key issue is the role of feasibility in whether each constituent criterion is necessary.

        Specifically, if MUTP is feasible, it is possible to augment it with many fewer tests than those required by CUTPNFP or MNFP, and yet still detect the entire fault hierarchy. The situation is more complex if MUTP is infeasible. Where MUTP is infeasible, but CUTPNFP is feasible, MNFP is not needed at all. If both MUTP and CUTPNFP are infeasible, then MNFP is required. A key aspect of this paper is that the infeasibility arguments apply at the finegrained level of terms and literals, and hence CUTPNFP and, if needed, MNFP, can be used only where they are required.

        MUMCUT takes the direct approach of simply requiring all three constituent criteria. This certainly works, but it is expensive. CUTPNFP and especially MNFP demand large numbers of tests, but, as hinted at above, turn out to be necessary only in relatively few cases.

          The contributions of this paper are:

1) Uses an analysis of MUMCUT constituent criterion feasibility at the level of terms and literals. This analysis allows test set sizes to be reduced without sacrificing fault detection.

2) Provides a refinement of fault detection relationships in Lau and Yu’s hierarchy [9] based on constituent criterion feasibility from the MUMCUT criterion (Figure 3.1).

3) Presents a new logic coverage criterion, MinimalMUMCUT, as well as an algorithm to generate MinimalMUMCUT test sets.

4) Gives a case study that shows the reductions in test set size possible with Minimal-MUMCUT.

         The paper is organized as follows. The remainder of Section 1 reviews relevant Boolean logic terminology and related work in logic criteria. Section 2 reviews MUMCUT and the three constituent criteria MUTP, CUTPNFP, and MNFP. Section 3 reviews the fault hierarchy. Section 4 develops the results explaining the impact of infeasibility on fault detection, presents algorithms to determine feasibility for each criterion at the level of terms and literals, and finally synthesizes these results into the Minimal-MUMCUT algorithm. Section 5 is a case study to assess the reduction in test set size provided by MinimalMUMCUT. Section 6 discusses how this work relates to more general issues in testing, and section 7 concludes the paper.

چکیده

1. مقدمه

1 .1 مجموعه اصطلاحات منطق بولین

2. 1 کار مرتبط

2. معیار منطق

1 .2 MUTP

2 .2 MNFP

3. 2 CUTPNFP

4 .2 MUMCUT 

3. آزمون‌های منطقی و سلسله مراتب نقص

4. استفاده از امکان‌سنجی معیار برای ارزیابی تشخیص نقص

5. ارزیابی تجربی

6. زمینه

7. نتیجه‌گیری

منابع

Abstract

1. Introduction

1.1 Boolean Logic Terminology

1.2 Related Work

2. Logic Criteria

2.1 MUTP

2.2 MNFP

2.3 CUTPNFP

2.4 MUMCUT

3. Logic Tests and Fault Hierarchy

4 Using Criterion Feasibility to Assess Fault Detection

5 Empirical Evaluation

6 Context

7 Conclusion

References