دانلود رایگان مقاله تکنیک کوانتومی برای کنترل دسترسی در محاسبات ابری

چکیده

            این دومین مقاله از مجموعه مقالات مربوط به کنترل دسترسی است که با مشکلات در محاسبات ابری با اتخاذ تکنیک های کوانتومی سروکار دارد. در این مقاله ما کاربرد رمزنگاری کوانتومی و توزیع کلید کوانتومی در دسترسی به مشکل کنترل را مورد مطالعه قرار می دهیم. طرح رمزنگاری و پروتکل را برای توزیع کلید در تنظیمات مکانیک های طبقه بندی شده کوانتوم (CQM) تدوین و فرمولبندی می کنیم. زبان گرافیکی CQM در این مقاله استفاده می شود. این طرح / پروتکل کوانتومی که پیشنهاد می کنیم، دارای مزایای متعددی برای طرح ها / پروتکل های ارائه شده در حالت هنر برای همان هدف است. آنها از لحاظ اطلاعاتی در فن آوری کنونی امن و قابل اجرا هستند.

1. مقدمه

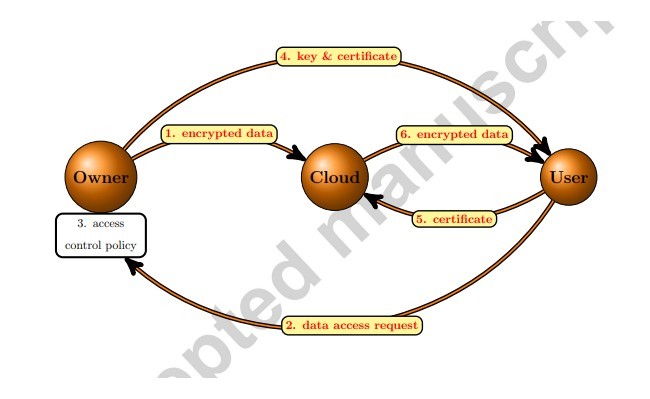
             این دومین مقاله از مجموعه مقالاتی است که با مسائل کنترل دسترسی در محاسبات ابری با اتخاذ تکنیک کوانتوم سروکار دارد [30]. مدلی ساده برای مسائل کنترل دسترسی در محاسبات ابری، که در شکل 1 نشان داده شده است مانند مالک داده، کاربر داده و ابر. صاحب داده، داده های رمزگذاری شده (بیت یا  کوبیت ها) را روی ابر قرار می دهد جائی که در آن کاربر بتواند دسترسی داشته باشد. به محض دریافت درخواست دسترسی به داده از جانب کاربر، مالک داده یک سیاست کنترل دسترسی را به منظور تصمیم گیری به کار می برد در مورد این موضوع که کاربر باید به دسترسی نفوذ پیدا کند. پس از آن، اگر سیاست کنترل دسترسی اظهار بر این داشته باشد که دسترسی باید به کاربر داده شود، پس مالک داده کلید مربوطه و تاییدیه را به کاربر ارسال می کند. در نهایت، به محض تائید موفقیت آمیز تاییدیه توسط ابر، کاربر تائیدیه را به ابر می فرستد و داده های رمزگشایی شده را بدست می آورد.

           در اولین مقاله این مجموعه [30]، استدلال ضروری کوانتومی را بعنوان یک زبان رسمی برای مشخص کردن سیاست های کنترل دسترسی توسعه می دهیم، که به مالک در تصمیم گیری اینکه آیا برای دسترسی به کاربر مجوز دهد یا نه کمک می کند. اما چگونه به کاربر دسترسی مطمئن داده می شود؟ رمزنگاری ابزار مناسبی را برای حل این مشکل ارائه می کند. بسیاری از راه حل های رمزنگاری برای مشکل  اعطای دسترسی پیشنهاد شده است [2، 6، 7، 8، 23، 24]. ایده اصلی این است: ابتدا تمام منابع را رمزگذاری کنید، سپس کلیدهایی را برای رمزگشایی به کاربرانی که اجازه دسترسی دارند اختصاص دهید. بطور دقیق تر، فرض کنید منابع   را داریم، سپس کلیدی را به یک کاربر اختصاص می دهیم البته اگر کاربر اجازه دسترسی به آن را داشته باشد. بنابراین، رمزگذاری و توزیع کلید نقش مهمی را در اعطای دسترسی ایفا می کند. در این مقاله، تکنیک های کوانتوم برای رمزنگاری و توزیع کلید را با استفاده از چارچوب ماشین های کوانتوم دسته بندی شده (CQM) توسعه می دهیم.

           ساختار بقیه این مقاله به شرح زیر است: در بخش 2 دانش پس زمینه در ماشین های کوانتوم دسته بندی شده را ارائه می کنیم. بنابراین رمزگذاری را با مشاهدات مکملانه در بخش 3 معرفی می کنیم. در  بخش 4 پروتکل کوانتومی خودمان را برای توزیع کلید ارائه می کنیم. در بخش 5 آثار مرتبط را بحث میکنیم و در بخش 6 مقاله نتیجه گیری می شود.

2. مکانیک کوانتومی طبقه بندی شده 

           مکانیک کوانتومی طبقه بندی شده [1، 16، 17، 11، 4، 13، 14] مربوط به مطالعه محاسبات کوانتومی و پایه های کوانتومی با استفاده از نظریه طبقه بندی، همچنین به عنوان زبان گرافیکی نزدیک به موضوع نظریه طبقه بندی شده است. ترکیب بندی سیستم های کوانتومی در CQM به عنوان یک پیوند اولیه قلمداد می شود که به راحتی با قلاب دسته بندی مونوایدال متقارن († -SMC) توصیف می شود.

2.1 نظریه دسته ها

تعریف 1 (دسته).A رده C شامل موارد زیر است:

1. مجموعه ob (C) از اشیاء،

2. برای هر جفت اجسام A، B، یک مجموعه C (A، B) از مورفیزم ها،

3. برای هر جسم A، یک مورفیسم باهویت خاص: 1A ∈ C (A، A),

4.عملیات ترکیب ترتیبی برای مورفیسم ها:

◦ : C(B,C) × C(A,B) → C(A,C),

برآورده نمودن شرایط زیر:

(1) ◦ در مورفیسم ها وابسته است: (h ◦ g) ◦ f = h ◦ (g ◦ f)

(2) ◦ در مورفیسم های متحرک است: 1B ◦ f = f = f ◦ 1A، برای همه f ∈ C (A، B).

         می توانیم به صورت گرافیکی اشیا را مانند سیم ها و مورفیسم ها ارائه دهیم وسیم ورودی و سیم خروجی مانند گره ها به هم متصل می شوند .این نمودارها از پایین به بالا خوانده می شوند. در این زبان گرافیکی شرایط ترکیب ترتیبی، یکپارچگی و وابستگی بی اهمیت می شود.

Abstract

          This is the second paper of the series of papers dealing with access control problems in cloud computing by adopting quantum techniques. In this paper we study the application of quantum encryption and quantum key distribution in the access control problem. We formalize our encryption scheme and protocol for key distribution in the setting of categorical quantum mechanics (CQM). The graphical language of CQM is used in this paper. The quantum scheme/protocol we propose possesses several advantages over existing schemes/protocols proposed in the state of the art for the same purpose. They are informationally secure and implementable by the current technology.

1. Introduction

          This is the second paper of the series of papers dealing with access control problems in cloud computing by adopting quantum technique [30]. A simple model for the access control problem in cloud computing is shown in Fig. 1. Such a model has three components: data owner, cloud and data user. The data owner places on the cloud the encrypted data (bit or qubits) which the user wants to access. Upon receiving a data access request from the user, the data owner employs an access control policy to decide whether the user should be granted the access. Afterwards, if the access control policy says that the access should be granted to the user, then the data owner sends the corresponding key and a certificate to the user. Finally, the user sends the certificate to the cloud and gets the encrypted data, upon the successful verification of the certificate by the cloud.

         In the first paper of this series [30], we developed quantum imperative logic as a formal language for the specification of access control policies, which helps the owner in deciding whether to grant access to the user or not. But how to grant certain access to a user? Cryptography offers a convenient tool for solving this problem. Many cryptographic solutions to the access-granting problem have been proposed [2, 6, 7, 8, 23, 24]. The basic idea is: first encrypt all resource, then assign keys for decryption to those users who are permitted to access. More precisely, suppose we have resources {data1, ... , datan}. We first use key1, ... , keyn to encrypt those data. So we have Enckey1 (data1), ... , Enckeyn (datan). Then we assign keyi to a user iff the user is permitted to access datai. Therefore, encryption and key distribution plays a pivotal role in granting access. In this paper, we develop quantum techniques for encryption and key distribution, using the framework of categorical quantum mechanics (CQM).

         The structure of the rest of this paper is as follows: we provide some background knowledge on categorical quantum mechanics in Section 2. Then we introduce encryption by complementary observables in Section 3. We present our quantum protocol for key distribution in Section 4 . We discuss related works in Section 5 and conclude this paper in Section 6.

2. Categorical quantum mechanics

         Categorical quantum mechanics [1, 16, 17, 11, 4, 13, 14] concerns the study of quantum computation and quantum foundations using category theory, as well as the graphical language closely related to category theory. Composition of quantum systems in CQM is treated as a primitive connective, which is conveniently described by dagger symmetric monoidal category (†-SMC).

2.1. Category theory

         Definition 1 (category). A category C consists of:

1. a collection ob(C) of objects,

2. for every pair of objects A, B, a set C(A, B) of morphisms,

3. for every object A, a special identity morphism: 1A ∈ C(A, A),

4. sequential composition operation for morphisms: ◦ : C(B, C) × C(A, B) → C(A, C),

satisfying the following conditions: (1) ◦ is associative on morphisms: (h ◦ g) ◦ f = h ◦ (g ◦ f),

(2) ◦ is unital on morphisms: 1B ◦ f = f = f ◦ 1A, for all f ∈ C(A, B).

         We can graphically represent objects as wires and morphisms as nodes attached with an input wire and an output wire. Those graphs are read from bottom to top. In this graphical language the conditions of sequential composition, associativity and unitality become trivial.

چکیده

1. مقدمه

2. مکانیک کوانتومی طبقه بندی شده 

2.1 نظریه دسته ها

2.2 جبر Frobenius و قابل مشاهده

 3 . رمزگذاری توسط تعریف مشاهدات مکمل

3.1 تعریف مکمل قابل مشاهده

3.2 رمزگذاری توسط تغییر فاز براساس مشاهدات مکمل

4.توزیع کلید: پروتکل سه فازه تعمیم یافته کوانتوم

5. اثر مرتبط

6. نتیجه گیری

منابع

Abstract

1. Introduction

2. Categorical quantum mechanics

2.1. Category theory

2.2. Frobenius algebra and observable

3. Encryption by complementary observables

3.1. Complementary observable

3.2. Encryption by phase shift over complementary observables

4. Key distribution: generalized quantum three-pass protocol

5. Related work

6. Conclusion

Reference