دانلود رایگان مقاله یک روش شناسایی بخش مجزای سریع بر پایه KNN و الگو گرفته از MST

چکیده

             پایگاه های داده ی دنیای واقعی امروزی معمولا شامل میلیون ها مورد با هزاران حوزه می شوند. به عنوان یک نتیجه، روش های شناسایی بخش جدای سنتی توزیع بنیان دارای توانایی های محدود شده ی بسیاری هستند و رویکردهای جدید همسایه های نزدیکترین K بنیان، محبوب تر شده اند. اما، مشکل با این روش های همسایه های نزدیکترین K بنیان این است که آنها بسیار به مقدار K حساس هستند(می توانند رتبه بندی متفاوتی برای بخش های مجزای برتر n داشته باشند)، از نظر محاسباتی برای مجموعه های داده بسیار پر هزینه هستند و در کل در اینکه آیا آنها برای مجموعه های ابعاد زیاد به خوبی کار می کنند یا نه شک وجود دارد. در این مقاله برای تا حدی دور زدن این مشکلات،یک فاکتور جدید بخش مجزای سراسری و یک فاکتور جدیدی بخش مجزای محلی و یک الگوریتم شناسایی بخش مجزای کارآمد بر مبنای این دو فاکتور مطرح کردیم که به راحتی پیاده سازی می شود و با راه حل های موجود می تواند عملکردهای رقابتی را بهبود ببخشد.آزمایشات انجام شده روی هر دو مجموعه های داده ی ترکیبی و واقعی، کارآمدی روش ما را نشان می دهند.

1. مقدمه

             شناسایی بخش مجزا با هدف گذاری برای کشف مشاهدات بسیار دور شده از سایر مشاهدات (به میزانی که شک هایی به وجود آید مبنی بر این که این مشاهات بوسیله ی مکانیزم متفادتی ایجاد می شوند) تبدیل به یک کار داده کاوی مهم شده است. شناسایی بخش مجزا با مورد استفاده قرار گرفتن در حوزه های متعدد مختلفی مانند شناسایی نفوذ برای امنیت سایبری، شناسایی تقلب برای کارت های اعتباری، بیمه و مالیات، شناسایی سریع شیوع بیماری در حوزه ی پزشکی، شناسایی خطا در شبکه ی سنسور برای نظارت سلامت، ترافیک، وضعیت ماشین، هوا، آلودگی و مراقبت  و غیره ، منافع بسیار زیادی را تولید کرده و در سال های اخیر روش های بسیاری برای این هدف ایجاد شده است، که از میان آنها می توان رویکردهای توزیع بنیان، عمق بنیان، فاصله بنیان، تراکم بنیان و خوشه بندی بنیان را نام برد.

              آخرین الگوریتم شناسایی بخش مجزا بر پایه ی نزدیک ترین k همسایه(مانند تعدادی از روش های فاصله بنیان و تراکم بنیان) راه های مختلفی برای فیلتر کردن داده ی عادی و موقعیت یابی تعداد کم بخش های مجزا نشان داده اند. در حالیکه این روش ها برای پیاده سازی ساده هستند اما سایر جنبه های مربوط به الگوریتم ها نیز ارزش تحقیقات بیشتر را دارند. اولا، این روش ها معمولا تنها n بخش مجزای برتر را با دو مقدار نشان می دهند. یکی از این مقادیر فاکتور بخش مجزا (به عنوان امتیاز نیز در این مقاله به آن اشاره شده) و دیگری رتبه بندی نقاط براساس امتیازات. بنابراین، روش های مختلف می توانند برای n بخش مجزای برتر، رتبه بندی های مختلفی داشته باشند. دوما، مشاهده شده که روش های شناسایی بخش مجزا بر مبنای نزدیک ترین k همسایه به پارامتر k حساس هستند و تغییری کوچک در k می تواند منجر به تغییرات در امتیازات و متقابلا رتبه بندی شود. به عنوان یک نتیجه، به جز برای بخش های مجزای خیلی قوی که امتیازات در آنها متمایز هستند، رتبه بندی نیز به k حساس است. سوما، برای مجموعه داده های بزرگ مدرن با N واحد داده، زمان اجرای   ، که برای جستجوی دقیق همسایه های k بوده، باید به طور معناداری بهبود داده شود. در نهایت، در فضا با بعد بالا، نقاط داده به طور برابر به یکدیگر نزدیک می شوند و مشکلی که "نفرین ابعاد" نامیده می شود را به وجود می آورند و این مسئله وجود دارد، چه ایده ی این تعاریف بخش مجزا برای داده ی بعد زیاد هنوز معنادار باشند و چه نباشد.

              در این مقاله یک روش شناسایی بخش مجزای الهام گرفته از درخت پوشای کمینه و KNNبنیان برای بر طرف کردن این چالش ها و برای تحقیق در مورد اثر ابعاد روی این الگوریتم های شناسایی بخش مجزای K-NN بنیان مطرح کرده ایم که کار ارائه شده در 9 را ادامه می دهد و هم از نظر محاسباتی کارآمد است و به شایستگی آخرین روش های شناسایی بخش مجزا می باشد.اساسا، روش ما با یافتن نزدیک ترین k همسایه برای هر نقطه ی داده شروع می کند. در ادامه یک MST کوچک برای هر نقطه ی داده و نزذیک ترین همسایه های k آن ساخته می شود. در نهایت تعداد کمی از بخش های مجزای با استفاده از امتیازهای بخش مجزای پیشنهاد شده ی ما، نسبتا در داخل MST کوچک شناسایی می شوند. اینکه یک نقطه ی خوب از روش های شناسایی بخش مجزای خوشه بندی بنیان MST هنگام خوشه بندی در حساب کردن فاصله ی بین نقاط داده در MST  و از همین رو کم کردن حساسیت امتیازات به k قرار دارد (به جای فاصله تا نزدیکترین همسایه (ها)به k یا k امین همسایه(ها))، بر مبنای مشاهدات است. اما، ساخت یک MST دقیق، نیازمند زمان اجرای درجه ی دو است و از نظر محاسباتی برای مجموعه داده های بزرگ بسیار گران است. بنابراین، هدف این پیوندزنی (برای مثال شناسایی بخش مجزای خوشه بندی بنیان و شناسایی بخش مجزای KNN بنیان) افزایش مقاومت و ثبات نتایج شناسایی و کاهش چشمگیر زمان محاسباتی برای روند شناسایی بخش مجزا بر پایه ی خوشه بندی MST است. اولین مشارکت ما در این مقاله، دو امتیاز ارائه شده ی جدید بخش مجزای KNN بنیان و با الهام از MST (یک سراسری و یک محلی) و یک روش شناسایی بخش مجزای ایجاد شده بر مبنای آنها است. دومین مشارکت بازدهی چشمگیر گام روش ارائه شده از طریق کاربرد یک تخمین کارآمدِ چارچوب جستجوی نزدیکترین همسایه های k برای روش های شناسایی بخش مجزای KNN بنیان ما است. این موضوع مزیتی برای کاری اولیه برای این تحقیق ارائه شده در 9 است که نیازمند ساخت یک زیر گراف کمینه ی تقریبی که به نمونه ی اصلی آن بسیار نزدیک باشد، است. سومین مشارکت ما، مطالعه ای در مورد مجموعه ای از الگوریتم های شناسایی بخش مجزای کنونی در زمانی است  که برای مجموعه داده های با ابعاد بالا استفاده شده اند. در نهایت، الگوریتم ما برای اینکه تا جای ممکن جامع باشد، ملزومات خاصی در مورد ابعاد مجموعه های داده ندارد و می تواند در شناسایی بخش های مجزای مجموعه داده هایی با ابعاد بالا به کار گرفته شود. تعدادی آزمایش روی هر دو مجموعه داده ی مصنوعی و واقعی، استقامت و کارآمدی رویکرد ارائه شده را در مقایسه با برخی از الگوریتم های شناسایی بخش مجزای مدرن نشان داده است.

             باقی این مقاله به صورت پیش رو سازمان دهی شده است. در بخش 2، برخی از کارهای موجود در مورد رویکردهای شناسایی بخش های مجزای مدرن را بررسی کرده ایم. در ادامه رویکردهای پیشنهاد شده ی خودمان را در بخش 3 ارائه می کنیم. در بخش 4 یک مطالعه ی تجربی انجام داده می شود. در نهایت نتیجه گیری در بخش 5 گرفته شده است.

2. کارهای مرتبط

          کارهای مرتبط در این مقاله، به سه دسته ی اصلی تقسیم بندی می شود: روش های شناسایی بخش مجزای تراکم و فاصله بنیان، روش های شناسایی بخش مجزا بر مبنای خوشه بندی MST و روش های شناسایی بخش مجزا برای داده با ابعاد بالا.

2.1. روش های شناسایی بخش مجزای تراکم و فاصله بنیان

             تلاش های زیادی به شناسایی بخش های مجزا تخصیص داده شده است. روش شناسایی بخش مجزای فاصله بنیان در اصل بوسیله ی Knorr and Ng در سال 1998 به عنوان یک پیشرفت در روش های توزیع پایه، ارائه شد. با توجه به مقیاس فاصله ی تعریف شده در یک فضای ویژگی، "یک شیء O در یک مجموعه داده ی T یک بخش مجزای DB(p,D) است اگر حداقل یک شکاف p اشیاء در T بزرگتر از فاصله ی D از O باشد"، که اصطلاح بخش مجزای DB(p,D) یک نماد مختصر برای بخش مجزای فاصله بنیان (بخش مجزای DB) شناسایی شده با استفاده از پارامترهای p و D است. KNN بنیان های گوناگونی برای متناسب بودن با اهداف مختلف عملی و تئوری ایجاد شده اند. "با توجه به دو عدد صحیح (n و k)، بخش های مجزای فاصله بنیان، واحدهایی از داده است که فاصله یآنها تا نزدیک ترین همسایه ی k ام آنها در میان n فاصله ی بزرگ است" (که در ادامه به عنوان “DB-MAX” ذکر شده است) و "با توجه به دو عدد صحیح (n و k)، بخش های مجزای فاصله بنیان، واحدهای داده ای هستند که میانگین فاصله ی آنها به نزدیک ترین k همسایه در میان n فاصله ی بزرگ است" (که در ادامه به عنوان “DB” ذکر شده است).

           اگر چه روش های شناسایی بخش مجزای فاصله بنیان به صورت ساده و ظریف و خوب برای مجموعه داده هایی که شامل یک خوشه یا بیشتر و با تراکم های مشابه کار می کنند و می توانند بخش های مجزای سراسری محور را شناسایی کنند اما برخی از مجموعه های داده ی دنیای واقعی معمولا ساختارهای پیچیده ای دارند. یک وضعیت کلاسیک که این کمبود را نشان می دهد، در شکل 1 نشان داده می شود که o1 و o2 بخش های مجزای سراسری هستند و می توانند به سادگی بوسیله ی روش های فاصله بنیان شناسایی شوند در حالیکه o3 بخش مجزای محلی است و نمی توانند به سادگی بوسیله ی روش های فاصله بنیان شناسایی شوند.

Abstract

            Today's real-world databases typically contain millions of items with many thousands of fields. As a result, traditional distribution-based outlier detection techniques have more and more restricted capabilities and novel k-nearest neighbors based approaches have become more and more popular. However, the problems with these k-nearest neighbors based methods are that they are very sensitive to the value of k, may have different rankings for top n outliers, are very computationally expensive for large datasets, and doubts exist in general whether they would work well for high dimensional datasets. To partially circumvent these problems, we propose in this paper a new global outlier factor and a new local outlier factor and an efficient outlier detection algorithm developed upon them that is easy to implement and can provide competing performances with existing solutions. Experiments performed on both synthetic and real data sets demonstrate the efficacy of our method.

1. Introduction

                Aiming to discover observations that deviate from other observations so much as to arouse suspicions that they are generated by a different mechanism, outlier detection has become an important data mining task [1]. Being applied in many different fields such as intrusion detection for cyber-security [2,3], fraud detection for credit cards, insurance and tax [4], early detection of disease outbreaks in the medical field [5], fault detection in sensor networks for monitoring health, traffic, machine status, weather, pollution, surveillance [6], and so on [7,8], it has generated enormous interests and many techniques have been developed for this purpose in recent years, namely distribution-based approaches, depth-based approaches, distance-based approaches, density-based approaches and clustering-based approaches.

             State-of-the-art k-nearest neighbors (kNN) based outlier detection algorithms, such as many distance-based and density-based methods, have demonstrated various ways to filter out the normal data and locate the small number of outliers. While they are simple to implement, other aspects concerning the algorithms are worth further exploration. Firstly, these methods usually return only top n outliers with two values. One is the outlier factor (also referred to as score in this paper) and the other is the ranking of the points according to the scores. Therefore, different methods may have different rankings for top n outliers. Secondly, it has been observed that k-nearest neighbors based outlier detection methods are sensitive to the parameter k and a small change in k can lead to changes in the scores and, correspondingly, the ranking. As a result, except for very strong outliers where the scores are distinct, the ranking is sensitive to k as well. Thirdly, for modern large datasets with N data items, the O(N log N) running time involved in the exact search of the k-nearest neighbors has to be improved significantly. Finally, in high dimensional space, data points become equally close to each other, raising the so-called problem of “curse of dimensionality”, and the issue exists whether the notion of these outlier definitions is still meaningful for the highdimensional data.

             To meet these challenges and to explore the impact of dimensionality on these kNN-based outlier detection algorithms, in this paper, we propose a new minimum spanning tree (MST)-inspired k-nearest neighbors (kNN)-based outlier detection method that continues the work presented in [9] and is both computationally efficient and competent with the state-of-the-art outlier detection techniques. Basically, our method starts by finding k-nearest neighbors for each data point. Then a mini MST is constructed upon each data point and its k-nearest neighbors. Finally a small number of outliers are identified relatively within each mini MST using our proposed outlier scores. It is based on the observation that one good point of MST clusteringbased outlier detection methods reside in its taking distances between data points in an MST (rather than the distances to the kth or k nearest neighbor(s)) into account when clustering, thus making the outlier scores relatively less sensitive to k. However, the construction of an exact MST requires quadratic running time and is very computationally expensive for modern large datasets. Therefore, the aim of this hybridization (i.e., MST clustering-based outlier detection and kNN based outlier detection) is to increase the robustness and consistency of the detecting results and to significantly decrease the computation time of MSTclustering based outlier detection process. Our first contribution in this paper is two newly proposed MST-inspired kNN-based outlier scores, a global one and a local one, and an outlier detection method developed upon them. Our second contribution is the significant tempo efficiency of the proposed method through the application of an efficient approximate k-nearest neighbors’ search framework to our kNN-based outlier detection techniques. This is an advantage over a preliminary work of this research presented in [9], which requires a construction of an approximate minimum spanning tree very close to a true one. Our third contribution is a study of a set of current outlier detection algorithms when applied to some high dimensional datasets. Finally, to be as general as possible, our algorithm has no specific requirements on the dimensionality of data sets and can be applied to outlier detection in large highdimensional data sets. A number of experiments on both synthetic and real data sets demonstrate the robustness and efficiency of the proposed approach in comparison with several state-of-the-art outlier detection algorithms.

            The rest of the paper is organized as follows. In Section 2, we review some existing work on state-of-the-art outlier detection approaches. We then present our proposed approaches in Section 3. In Section 4, an empirical study is conducted. Finally, conclusions are made in Section 5.

2. Related work

           Related work in this paper falls into three main categories: distance -and density-based outlier detection methods, MST clustering-based outlier detection techniques, and outlier detection techniques for high dimensional data.

2.1. Distance-based and density-based outlier detection

           Many efforts have been devoted to detecting outliers. Distance-based outlier detection method was originally proposed by Knorr and Ng in 1998 as an improvement over distribution based methods. Given a distance measure defined on a feature space, “an object O in a dataset T is a DB(p,D)-outlier if at least a fraction p of the objects in T lies greater than distance D from O”, where the term DB(p, D)-outlier is a shorthand notation for a Distance-Based outlier (DB-outlier) detected using parameters p and D [10]. To suit for different theoretical and practical purposes, two kNN-based variants have been developed. “Given two integers, n and k, Distance-Based outliers are the data items whose distance to their kth nearest neighbor is among top n largest ones [11]” (referred to as “DB-MAX” in the following), and “Given two integers, n and k, Distance-Based outliers are the data items whose average distance to their k-nearest neighbors is among top n largest ones [12]” (referred to as “DB” in the following).

           Though simple and elegant, distance-based outlier detection techniques work well for data sets that contain one or more clusters with similar densities and can detect more globally-orientated outliers. However, many real world data sets often have complex structures. A classic situation illustrating this deficiency is shown in Fig. 1, where o1 and o2 are global outliers and can easily be detected by distance-based methods while o3 is a local one and cannot.

چکیده
1. مقدمه
2. کارهای مرتبط
2.1. روش های شناسایی بخش مجزای تراکم و فاصله بنیان
2.2. الگوریتم هایی بر مبنای خوشه بندی MST
2.3. بخش مجزا کاوی با ابعاد بالا بر مبنای طرح
3. یک الگوریتم شناسایی بخش مجزا ی الگو گرفته از MST
3.1. دو عامل جدید بخش مجزا
3.2. ساختار جستجوی نزدیک ترین همسایه تخمینی
3.3. الگوریتم شناسایی بخش مجزا ی الهام گرفته از MST ما
3.4. تحلیل پیچیدگی زمان
3.5.  شبه کد برای DHCA
4. یک مطالعه عملکرد
4.1. عملکرد الگوریتم ما در مجموعه داده های ترکیبی
4.2. عملکرد روی مجمو عه های داده ی واقعی
4.2.1. داده لیمفوگرافی
4.2.2. داده شاتل فضایی
4.2.3. داده یونوسفر
4.2.4. ارقام نوری
4.2.5. ویژگی های چندگانه
4.3. عملکرد الگوریتم ما با SOM-TH
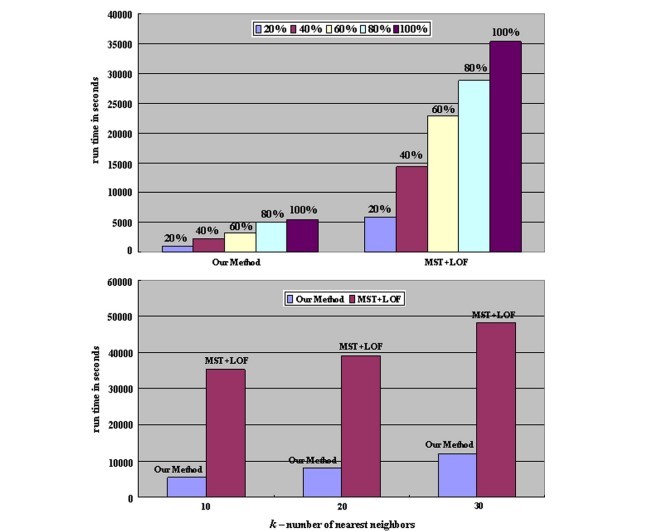
4.4. عملکرد زمان راه اندازی برای الگوریتم ما روی مجموعه داده هایی با ابعاد بالا
5. نتیجه گیری
منابع

Abstract
1. Introduction
2. Related work
2.1. Distance-based and density-based outlier detection
2.2. MST clustering-based algorithms
2.3. Projection based High dimensional outlier mining
3. An MST-inspired outlier detection algorithm
3.1. Two new outlier factors
3.2. An approximate nearest neighbor search structure
3.3. Our MST- inspired outlier detection algorithm
3.4. Time complexity analysis
3.5. Pseudo code for DHCA
4. A performance study
4.1. Performance of our algorithm on synthetic datasets
4.2. Performance on real datasets
4.2.1. Lymphography data
4.2.2. Space shuttle data
4.2.3. Ionosphere data
4.2.4. Optical digits
4.2.5. Multiple features
4.3. Performance of our algorithm with SOM-TH
4.4. Run time performance of our algorithm on large High-dimensional datasets
5. Conclusion
References