دانلود رایگان مقاله ارزیابی کمی سیر تکامل ضریب تاثیر علمی شخصی

معرفی

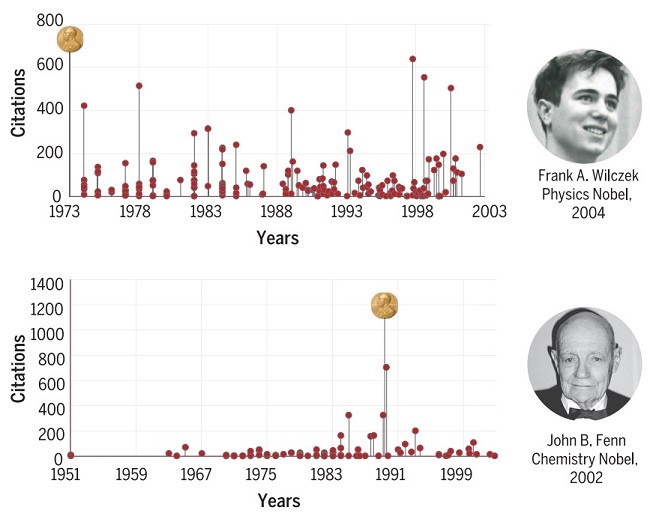
     در اغلب جنبه های عملکرد بشری، از ورزش تا مهندسی، مسیر پیشرفت خوب به منحنی یادگیری تند و تلاش طولانی نیازمند است. علم نیز از این قاعده مبرا نیست: اکتشافات برجسته اغلب بر نشریات با تاثیر کمتر مقدم بوده است. اما صرف نظر از تمایل رو به رشد برای تشخیص دانشمندان خوب تاکنون، الگوهای تخصصی جدیدی که مزیت علمی را مشخصه بندی نماید ناشناخته باقی مانده است. 

انگیزه اساسی تحقیق

     چگونه تاثیر و بهره وری در یک تخصص علمی تغییر خواهد کرد؟ آیا ضریب تاثیر که معمولا شایعترین معیار بازدهی علمی مربوطه است، از الگوهای پیش بینی شده ای پیروی خواهد کرد؟ آیا می توانیم زمان رسیدن یک دانشمند به موفقیتی برجسته را تخمین بزنیم؟ آیا می توانیم تخصص علمی را از لحاظ کمی و مولفه های تخمینی مدلسازی نماییم؟ با این سوالات ارائه شده، در اینجا به بررسی کمی سیر تکامل ضریب تاثیر و بهره وری در بین هزاران کار علمی خواهیم پرداخت. این کار را با بازبینی تاثیر بلندمدت روی جامعه علمی که براساس معیار تعداد نقل قول از مقالات مشخص شده است، در نشریات ثبت شده علمی از هفت رشته مختلف انجام خواهیم داد. 

نتایج

     به این نتیجه رسیدیم که کار با بالاترین تاثیر در دوره کاری یک دانشمند به طور تصادفی در بدنه کارهای او توزیع شده است.  به این معنا که کار با بالاترین تاثیرگزاری با احتمال یکسان می تواند هرجایی از زنجیره مقالات منتشرشده توسط یک داشنمند باشد- یعنی اولین انتشار، در اواسط دوره کاری، یا آخرین انتشار او باشد. این قانون تاثیر تصادفی، برای دانشمندان رشته های مختلف با دوره تخصصی متفاوت، در حال کار در دهه های مختلف، با انتشار انفرادی یا تیمی و با تایید اعتبار علمی یکنواخت یا متفاوت بین همکاران، صادق است. 

     قانون تاثیر تصادفی به ما این امکان را خواهد داد که یک مدل کمی را توسعه دهیم که به صورت متقارن قانون بهره وری و موفقیت در هر رشته علمی را روشن سازد. در این مدل فرض بر این است که هر دانشمند یک پروژه را با تاثیر تصادفی p انتخاب کرده و با یک ضریب Qi آن را بهبود می بخشد و منتج به انتشاری با تاثیر گذاری Qip می شود. پارامتر Qi قابلیت دانشمند i برای پیشرفت دانش دردسترس، به طریقی است که تاثیر احتمالی p یک مقاله را بهبو   (Qi > 1) یا کاهش (Qi < 1) دهد. این مدل پیش بینی می کند که اکتشافات با تاثیر حقیقی بالا به ترکیبی از Qi و  p بالا نیازمندند و بهره وری زیاد به تنهایی نمی تواند شانس ایجاد یک کار با تاثیرگزای خیلی زیاد را بهبود بخشد. همچنین نشان می دهیم که Q دانشمند که نشان دهنده توانایی شخصی برای انتشار مقالات با تاثیر بالاست، مستقل از مرحله تخصصی او می باشد. این مورد در تقابل با معیارهای کنونی، شامل تعداد کلی نقل قول ها تا مقیاس-h است که با زمان افزایش خواهند یافت. مدل Q توصیفی تجربی از این معیارهای تاثیر سنتی ارائه می کند، به ما امکان پیش بینی سیر تکاملی آینده هر دانشمند را می دهد و دستیابی به معیارهای رسمی نظیر جوایز نوبل را پیش بینی خواهد کرد.

مدل تاثیر تصادفی (R-model)

     می توانیم از قانون تاثیر تصادفی برای ساختن یک مدل خنثی از کارهای تخصصی دانشمندان بهره ببریم: فرض می کنیم که هر دانشمند زنجیره مقالاتی منتشر می کند که تاثیرشان به طور تصادفی از توزیع تاثیر یکسان (P(c10)) انتخاب شده است. در نتیجه، تنها تفاوت بین دو دانشمند بهره وری کلی N آنهاست. با داشتن توزیع P(c10) و P(N) (شکل3، الف و ب) به عنوان ورودی، مدل R به دست آمده (بخش س4. 2) به طور دقیق تصادفی بودن زنجیره تاثیرگزاری P(N*/N) (شکل 2ای) را بازتولید خواهد کرد، اما دو تخمین را نیز ایجاد خواهد کرد که در تضاد با داده ها است.

     الف) بهره وری به تنهایی باعث موفقیت می شود: اگر تاثیر هر مقاله به طور تصادفی از P(c10) یکسان انتخاب شود، یک دانشمند بهره ور (با N بالا) تمایل بیشتری به داشتن امتیاز c*10 بالا خواهد داشت (معادلات س7 و س8 را ببینید) (26 و 27). اما مدل R به طور صحیح رشد مشاهده شده به عنوان تابعی از < c*10> را بازتولید نمی کند (شکل 3ث).

      ب) تاثیر واگرا : هرچه تاثیر میانگین انتشارات یک دانشمند بدون در نظرگرفتن انتشار با بیشترین نقل قول < c*10> (شکل 1الف) بالاتر باشد، تاثیر مقاله با بیشترین نقل c*10 بالاتر خواهد بود (شکل 3د). بنابراین، مقالات با تاثیر بالای حقیقی توسط دانشمندانی منتشر می شوند که ثبت پایداری از تاثیر بالا داشته اند. مدل R نمی تواند این رفتار را پیش بینی کند، بلکه تخمین می زند که وقتی (شکل 3د) < c*10> واگرا خواهد شد که این رفتار ناشی از ذات طبیعی لگاریتم است (بخش س4. 1 و شکل س27).

     نقص های الف و ب ما را برانگیخت تا این فرضیه را بگوییم که مقالات تحقیقی همگی از توزیع تاثیر مشابهی برداشته شده اند و بنابراین محققین هیچ تاثیر شخصی قابل تشخیصی ندارند و این مورد ما را مجبور کرد که رابطه بین بهره وری، تاثیر و شانس را به طور دقیقتر بررسی نماییم.

مدل Q

     متاسفانه در مدل R، دانشمندان با بهره وری یکسان تاثیر غیر قابل تشخیصی دارند. در واقعیت، تاثیر به طور قابل ملاحظه بین دانشمندان فرق دارد (شکل 3ای)، که وجود یک پارامتر پنهان Qi برای تعادل تاثیرگزاری را خاطرنشان می کند که برای هر دانشمند i مقدار واحدی دارد.

INTRODUCTION 

     In most areas of human performance, from sport to engineering, the path to a major accomplishment requires a steep learning curve and long practice. Science is not that different: Outstanding discoveries are often preceded by publications of less memorable impact. However, despite the increasing desire to identify early promising scientists, the temporal career patterns that characterize the emergence of scientific excellence remain unknown.

RATIONALE

     How do impact and productivity change over a scientific career? Does impact, arguably the most relevant performance measure, follow predictable patterns? Can we predict the timing of a scientist’s outstanding achievement? Can we model, in quantitative and predictive terms, scientific careers? Driven by these questions, here we quantify the evolution of impact and productivity throughout thousands of scientific careers. We do so by reconstructing the publication record of scientists from seven disciplines, associating to each paper its long-term impact on the scientific community, as quantified by citation metrics.

RESULTS

     We find that the highest-impact work in a scientist’s career is randomly distributed within her body of work. That is, the highest-impact work can be, with the same probability, anywhere in the sequence of papers published by a scientist—it could be the first publication, could appear mid-career, or could be a scientist’s last publication. This random-impact rule holds for scientists in different disciplines, with different career lengths, working in different decades, and publishing solo or with teams and whether credit is assigned uniformly or unevenly among collaborators.

     The random-impact rule allows us to develop a quantitative model, which systematically untangles the role of productivity and luck in each scientific career. The model assumes that each scientist selects a project with a random potential p and improves on it with a factor Qi, resulting in a publication of impact Qip. The parameter Qi captures the ability of scientist i to take advantage of the available knowledge in a way that enhances (Qi > 1) or diminishes (Qi < 1) the potential impact p of a paper. The model predicts that truly high-impact discoveries require a combination of high Q and luck (p) and that increased productivity alone cannot substantially enhance the chance of a very high impact work. We also show that a scientist’s Q, capturing her sustained ability to publish high-impact papers, is independent of her career stage. This is in contrast with all current metrics of excellence, from the total number of citations to the hindex, which increase with time. The Q model provides an analytical expression of these traditional impact metrics and allows us to predict their future time evolution for each individual scientist, being also predictive of independent recognitions, like Nobel prizes.

Random-impact model (R-model)

     We can rely on the random impact rule to build a null model of scientific careers: We assume that each scientist publishes a sequence of papers whose impact is randomly chosen from the same impact distribution P(c10). Consequently, the only difference between two scientists is their overall productivity N. With the observed P(c10) and P(N) distributions (Fig. 3, A and B) as input, the obtained R-model (section S4.2) accurately reproduces the randomness of the impact sequence P(N*/N) (Fig. 2E), but it also makes two predictions that are at odds with the data.

     (a) Productivity alone begets success: If each paper’s impact is randomly drawn from the same P(c10), a productive scientist (high N) will more likely score a high c10* (see eqs. S7 and S18) (26, 27). However, the R-model does not correctly reproduce the observed increase of hc10* i as a function of N (Fig. 3C).

     (b) Divergent impact: The higher the average impact of a scientist’s publications without the most-cited publication hc10 −* i (Fig. 1A), the higher the impact of the most-cited paper, c10* (Fig. 3D). Hence, papers with truly high impact are published by scientists with a consistent record of high impact. The R-model cannot account for this behavior, predicting that hc10* i diverges when hlog ðc10 −* Þi→1:97 (Fig. 3D), a consequence of the log-normal nature of P(c10) (section S4.1 and fig. S27).

     Failures (a) and (b) prompt us to abandon our hypothesis that research papers are all drawn from the same impact distribution and hence researchers have no distinguishable individual impact, forcing us to explore more closely the relationship between productivity, impact, and chance.

Q-model

     Crucially, in the R-model, scientists with similar productivity have indistinguishable impact. In reality, impact varies greatly between scientists (Fig. 3E), suggesting the existence of a hidden parameter Qi that modulates impact, which has a unique value for each scientist i.

معرفی

انگیزه اساسی تحقیق

نتایج

الگوهای تاثیر و بهره وری در تخصص های علمی

مدل تاثیر تصادفی (R-model)

مدل Q

سنجش و دقت پارامتر پنهان Q

توان تخمینی پارامتر پنهان Q

خلاصه و بحث

روش های جمع آوری داده

سنجش نقل قول ها

مدل Q

منابع

INTRODUCTION

RATIONALE

RESULTS

CONCLUSION

Productivity and impact patterns in scientific careers

Random-impact model (R-model)

Q-model

The measurement and accuracy of the hidden parameter Q

The predictive power of the hidden parameter Q

Summary and discussion

Methods Data sets

Citation measures

Q-model

REFERENCES AND NOTES