دانلود رایگان مقاله مدل دو پارامتری جهت شبیه سازی اثرات مادون قرمز حرارتی

چکیده

 
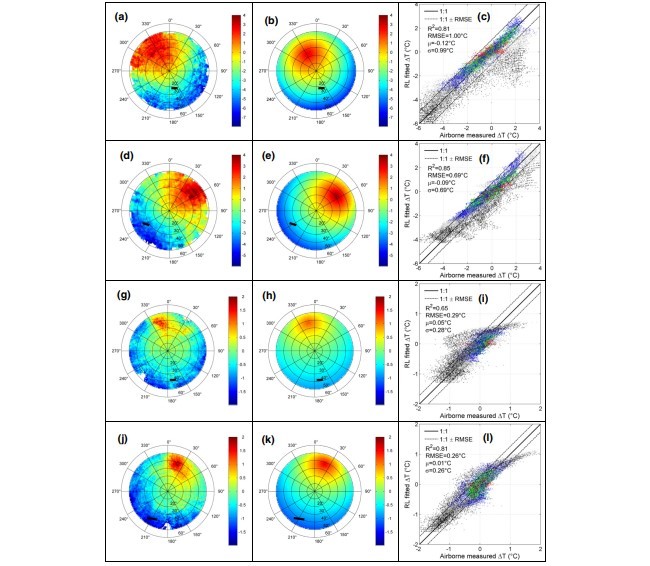
              اندازه گیری های دمای سطحی زمین (LST) که در دامنه مادون قرمز حرارتی (TIR) انجام می شود، در معرض نا همسانگردی جهتی شدید قرار داشته اند. به جای مدل های TIR فیزیکی تحلیلی دقیق که به اطلاعات ورودی و ظرفیت محاسباتی قابل توجه نیاز دارند، روش های پارامتریک ساده شده قادر به نشان دادن و اصلاح با دقت اثرات زاویه ای بر LST می باشند که برای کاربرد های اجرایی ماهواره نیز مناسب خواهند بود. ما در این تحقیق یک مدل دو پارامتری ساده تحت عنوان RL (روجین- لاگوارده) را که نشان دهنده قابلیت هایی جهت نشان دادن علائم جهتی کاربرد های شهری و گیاهی با دقت بهتر از 1 درجه می باشد، ارائه می کنیم. این مقدار نشان دهنده RMSE (خطای جذر مربعات میانگین) به دست آمده به عنوان بهترین توجیه مدل RL نسبت به مجموعه داده های موجود می باشد. سپس روش RL با یک مجموعه داده ترکیبی ایجاد شده توسط مدل مشاهده پوشش خاک، فتوشیمی و شار انرژی (SCOPE) ایجاد شده است به طوری که تغییرات گسترده در روش های هواشناسی،  سازه و ساختار سایبان و شرایط آب مد نظر قرار گرفته است. نتایج نشان دهنده RMSE≤0.6C می باشند که به عنوان یک نتیجه مناسب شناخته می شود. همچنین مدل RL از عملکرد بهتری حتی نسبت به مدل پارامتریک مشهور ونیکوو که دارای دو مجهول می باشد، برخوردار است. توانایی مدل RL جهت بازتولید بهتر پدیده نقطه داغ به بیان این خصوصیت می پردازد. 

               مدل RL به عنوان یک روش احتمالی برای زنجیره های پردازش عملیاتی داده های ماهواره ای TIR شناخته می شود، زیرا این مدل در برگیرنده الزامات هر دو فرمول بندی تحلیلی و تعداد محدود پارامتر های ورودی می باشد. با این حال بایستی تلاش ها جهت انجام روش های معکوس صورت پذیرد. 

1. مقدمه 

              اندازه گیری های مادون قرمز حرارتی (TIR) به طور گسترده جهت بازیابی دمای سطحی زمین (LST) انجام می شوند که به عنوان یک عاملی مفید جهت به دست آوردن جریان های سطحی به ویژه تبخیر و میعان مورد استفاده قرار می گیرند. با این حال این اندازه گیری ها در معرض اثرات ناهمسانگردی جهتی شدید قرار دارند. می توان این موارد را به صورت تفاوت بین دمای خارج از سمت القدم و دمای سمت القدم تعریف کرد. این تفاوت ها می توانند به بیش از 15 درجه بر اساس نظریات محققین مختلف برسند (کیمز و کیرشنر 1983، لاگوراد و همکاران ، 2014). 

             تلاش هایی در گذشته جهت مدل سازی ناهمسانگردی تابشی TIR در شرایط هندسی متناسب، انتقال تابشی، روش های 3 بعدی و پارامتریک انجام شده است. می توان این بررسی را در تحقیقات ورهوف و همکاران (2007) مشاهده کرد. دافور و همکاران (2015) اخیرا توانایی مدل انتقال خاک- گیاه- اتمسفر (SVAT) SCOPE را (ون در تال و همکاران 2009) که شرح دقیقی از هر دو فرآیند فیزیکی و فیزیولوژیکی جهت شبیه سازی ناهمسانگردی جهتی TIR ارائه می کند، نشان داده اند. در واقع پردازش داده های TIR قادر به اصلاح داده های سنجش از راه دور TIR از اثرات جهتی با استفاده از یک روش سریع محاسباتی می باشد. بدین ترتیب، الگوریتم هایی را با (1) نیاز به برخی از داده های ورودی و (2) قابل تفسیر بودن جهت سادگی در اجرا در زنجیره های پردازش داده های عملیاتی ماهواره مورد نیاز می باشند، ارائه کرده اند. ثانیا، مدل های ساده جهت ارزیابی سریع اثر نمونه برداری زاویه ای که در طراحی برنامه های آزمایشگاهی به منظور بهینه سازی پروتوکل تجهیزاتی به کار گرفته می شود، بسیار مفید می باشند. 

             مدل های پارامتریک ساده از کارایی بسیاری برخوردار می باشند. به دلیل تعداد پارامتر های ورودی محدود آنها، روش معکوس سازی از اهمیت بیشتری برخوردار می باشد. موضوع دیگر آن است که آنها می توانند در هر مقیاس مکانی به ویژه هنگامی که قابلیت خطی مدل امکان پذیر است، به کار گرفته شوند. علاوه براین، مدل های پارامتریک می توانند جهت اندازه گیری صدا نسبت به مدل های تعینی که تحت تاثیر عدم اطمینان های تجمعی پایگاه داده های ورودی بزرگ قرار می گیرند، بهتر عمل کنند. مدل های پارامتریک می توانند به صورت تجربی بوده و یا مبتنی بر فرضیات فیزیکی باشند. هر چند که مدل های پارامتریک به صورت گسترده جهت اصلاح BRDF اپتیکال (تابع توزیع انعکاسی دو جهتی) به صورت گسترده مورد استفاده قرار می گیرند، هنوز این روش جهت پردازش و تحلیل داده های TIR ارائه نشده است. با این حال یک محدودیت در این حوزه می تواند ناشی از اعمال مقادیر اولیه برای پارامتر های ورودی می باشد، مگر آن که مفهوم فیزیکی آنها به خوبی به وسیله آزمایشات محلی تعیین شود. 

            هنگام انجام اندازه گیری های ماهواره ای TIR به وسیله مدل سازی، یک فرض اصلی آن است که هر پیکسل حسگر به صورت جمع مقادیر فتومتریک اولیه می باشد. می توان این مورد را به صورت یک ترکیب خطی از توابع ریاضی ترسیمی به وسیله کرنل ها به صورت توابع مثلثی هندسه مشاهداتی مدل سازی کرد. در دامنه اپتیکال، روش کرنل به صورت موفقیت آمیز نشان دهنده BRDF می باشد (ونر و همکاران 1995؛ جاپ 2000؛ برون و همکاران 2002؛ ورموت و همکاران 2009). در حوزه TIR، این روش جهت شبیه سازی نا همسانگردی جهتی حساسیت سطحی به کار گرفته شده است (سیندر و ون 1998؛ سو و همکاران 2002). به منظور مدل سازی نا همانسگردی تابشی بر روی سیگنال TIR و همچنین دما از مشاهدات ماهواره های ثابت در زمین، وینیکو و همکاران (2012) یک مدل پارامتریک از ناهمسانگردی TIR را بر اساس تنها دو کرنل ارائه کرده اند. 

             به طور کلی، می توان حل مسئله معکوس را با ایجاد جداول LUT اولیه به جای شبیه سازی های مدل TIR پیچیده جهت اولویت بندی یادگیری ماشین ارائه کرد. حتی بر اساس اطلاعات ما، هنوز این امکان در دامنه TIR مورد ارزیابی قرار نگرفته است. با این حال، در حوزه کاربرد های کنترل از راه دور، کارایی راه حل به عنوان یک نگرانی واقعی جهت مطابقت با امکان نویز دار بودن و مشاهده داده های پراکنده به شمار می آید. 

            این موضوع توجیه کننده روش دیگر شامل به دست آوردن روابط تحلیلی صرف نظر از فرضیات ساده شده فیزیکی می باشد. به طور مثال روجین (2000) و برون و همکاران (2002) دو مدل از نقطه داغ را با ساده سازی روش های انتقال تابشی در داخل سایبان ها برای کاربرد های سنجش از راه دور اپتیکال ارائه کرده اند. در TIR، لاگوراده و ایروین (2008) مدل روجین (2000) را جهت به دست آوردن یک رابطه پارامتریک از ناهمسانگردی جهتی با نیاز به دو پارامتر معلوم اصلاح کرده اند. اولین آزمایش قابل قبول نسبت به اندازه گیری های آزمایشگاهی در سایبان شهری به دست آمد. سادگی مدل موجب جذاب شدن آن جهت بیان ناهمسانگردی جهتی شده است. 

           با این حال بایستی به صورت گسترده به بررسی این روش پرداخت. این موضوع هدف این مقاله می باشد. در بخش اول، مدل بیان شده و توانایی آن جهت شبیه سازی DA نسبت به گیاهان نشان داده می شود. کمبود پایگاه های داده DA آزمایشگاهی موجب ایجاد اطلاعات زاویه ای اوج و آزیموت و موجب ارزیابی قابلیت اطمینان مدل در گام دوم با ارزیابی آن نسبت به یک پایگاه داده ترکیبی ایجاد شده SCOPE به وسیله یک مدل تعینی می گردد. در این قسمت از SCOPE به عنوان یک تولید کننده داده برای شرایط واقعی که قابل برآورده شدن می باشند، استفاده می شود؛ ساختار سایبان، وضعیت آب، forcing هواشناسی. در نهایت بخش سوم مقایسه ای از را با روش وینیکو که جهت اصلاح داده های ماهواره برای اثراتDA  انجام می دهد. بر اساس اطلاعات ما، مدل وینیکو هیچ جایگزینی تا کنون نداشته است، از این رو قابلیت های دو روش برای سنجش از راه دور مورد بحث قرار می گیرند. 

 Abstract     

 Measurements of land surface temperature (LST) performed in the thermal infrared (TIR) domain are prone to strong directional anisotropy. Instead of detailed analytical physical TIR models requiring too much input information and computational capacities, simplified parametric approaches capable to mimic and correct with precision the angular effects on LST will be deemed suitable for practical satellite applications. In this study, we present a simple two parameters model, so-called RL (Roujean-Lagouarde), which shows capabilities to properly depict the directional signatures of both urban and vegetation targets within an accuracy better than 1 °C. This latter value is the RMSE (root mean square error) obtained as the best adjustment of the RL model against in situ datasets. Then the RL approach was compared to a synthetic dataset generated by the model Soil Canopy Observation, Photochemistry and Energy fluxes (SCOPE) in which large variability in meteorological scenarios, canopy structure and water status conditions was accounted for. Results indicate RMSE ≤0.6 °C which is a very hopeful result. Besides, the RL model performs even better than the popular parametric model of Vinnikov that encompasses two unknowns. The ability of RL model to better reproduce the hotspot phenomenon explains this feature.

             The RL model appears as a potential candidate for future operational processing chains of TIR satellite data because it fulfills the requirements of both simple analytical formulation and limited number of input parameters. Efforts nevertheless remain to be done on inversion methodologies.

1. Introduction

              Thermal infrared (TIR) measurements are widely used to retrieve land surface temperature (LST) which is a useful proxy to derive surface fluxes, especially evapotranspiration. However these measurements are prone to strong directional anisotropic effects. Those can be defined as the difference between off-nadir and nadir temperatures. Such difference can reach up to 15 °C according to various authors (Kimes and Kirchner, 1983; Lagouarde et al., 2014).

             Efforts have been made in the past to model the TIR radiation anisotropy in following geometric, radiative transfer, 3-dimensional and parametric approaches. A review can be found in Verhoef et al. (2007). Duffour et al. (2015b) recently demonstrated the ability of the Soil-Vegetation-Atmosphere Transfer (SVAT) model SCOPE (Van der Tol et al., 2009) which combines a detailed description of both physical and physiological processes to simulate TIR directional anisotropy. Actually, TIR data processing is in need of simple models for several purposes. First reason is to be able to correct TIR remote sensing data from directional effects using a fast and computationally efficient method. For such, one must only consider algorithms (i) requiring a few input data and (ii) being analytically interpretable for ease of implementation into operational satellite data processing chains. Secondly, simple models are very helpful for a rapid assessment of the impact of the angular sampling, which is particularly relevant for the design of experimental campaigns with the concern of optimizing the instrumental protocol.

          Simple parametric models are attractive in many ways. Because of their limited number of input parameters, the inversion procedure is more certain. Another asset is that they can be relevant at any spatial scale, in particular when linearity of the model is possible. Moreover, parametric models may be more robust to measurement noise compared to deterministic models which are affected by the cumulative uncertainties of the large input datasets they require. Parametric models can be totally empirical or based on physical assumptions. Although parametric models are widely used to correct optical BRDF (Bi-directional Reflectance Distribution Function), such an approach has not yet been developed so far to process and analyze TIR data. One limitation however would be the prescription of a priori values for the input parameters, unless their physical meaning may be well determined through field experiments for instance.

            When approaching TIR satellite measurements through modeling, a primary assumption is that any sensor pixel is the sum of dissociated elementary photometric quantities. These latter can be further modeled as a linear combination of mathematical functions sketched by kernels being trigonometric functions of the geometry of observation. In the optical domain, the kernel approach has been successful to mimic the BRDF (Wanner et al., 1995; Jupp, 2000; Bréon et al., 2002; Vermote et al., 2009). In the TIR domain, it has been applied to simulate the directional anisotropy of surface emissivity (Snyder and Wan, 1998; Su et al., 2002). In order to model the radiation anisotropy on TIR signal and further on temperature from geostationary satellites observations, Vinnikov et al. (2012) developed a parametric model of TIR anisotropy based on only two kernels.

            Generally speaking, the solution to the inverse problem may be obtained by generating first Look Up Tables (LUTs) issued from simulations of a sophisticated TIR model, at the cost of some training for initiate some machine learning. Even so, and to our knowledge, this possibility has not been evaluated yet in the TIR domain. However, in the context of remote sensing applications, the robustness of the solution is indeed a real concern in order to comply with possibly noisy and sparse observations.

           This justifies for another approach here consisting in the derivation of analytical expressions departing from simplified assumptions on the physics. For instance Roujean (2000) and Bréon et al. (2002) have proposed two models of hot spot simplifying the radiative transfer processes inside canopies for optical remote sensing applications. In the TIR, Lagouarde and Irvine (2008) adapted the Roujean (2000) model to derive a parametric expression of directional anisotropy requiring two parameters only to be known or adjusted. A first favorable test was obtained against experimental measurements acquired over an urban canopy. The simplicity of the model makes it very attractive to characterize the directional anisotropy.

          Nevertheless it still requires to be extensively evaluated. Such is the goal of this paper. In a first section, the model will be described and its ability to simulate DA over vegetation demonstrated. The scarcity of available experimental DA datasets providing both azimuth and zenith angular information led us to assess the reliability of the model in a second step by testing it against a synthetic dataset generated by a deterministic model, SCOPE. Here, SCOPE is used as a data generator, for a large range of realistic conditions that can be met: structure of the canopy, water status, meteorological forcing. A third section finally proposes a comparison with the Vinnikov's approach which was considered to correct satellite data for DA effects. Since to our knowledge, Vinnikov's model has no equivalent so far, the mutual assets of both approaches for remote sensing applications are further discussed.

چکیده
1. مقدمه 
2. مدل RL پارامتریک
2.1. فرمول بندی تحلیلی
2.1. ارزیابی آزمایشگاهی RL
2.1.1. داده های آزمایشگاهی
2.2.2. ارزیابی RL نسبت به یک سایبان شهری
2.2.3. ارزیابی RL نستب به یک سایبان جنگلی
3. تعمیم SCOPE
3.1. مدل SCOPE
3.2. ایجاد یک پایگاه داده ترکیبی
3.3. مقایسه RL و نا همسانگردی جهتی SCOPE
4. مقایسه بین قابلیت های RL و وینیکو
4.1. روش کرنل وینیکو
4.2. مقایسه بین قابلیت های RL و وینیکو
5. بحث 
5.1. محدودیت های روش های پارامتریک
5.2. کاربرد های RL در داده های ماهواره و محلی
5.2.1. ارزیابی کیفی اندازه گیری های محلی
5.2.2. ارزیابی کیفیت نا همسانگردی بر داده های ماهواره
5.2.3. اصلاح نا همسانگردی جهتی TIR در داده های مکانی
6. نتیجه گیری
منابع

Abstract
1. Introduction
2. The parametric RL model
2.1. Analytical formulation
2.2. Experimental evaluation of RL
2.2.1. Experimental data
2.2.2. Evaluation of RL over a urban canopy
2.2.3. Evaluation of RL over a forest canopy
3. SCOPE generalization
3.1. The SCOPE model
3.2. Generation of a synthetic dataset
3.3. Comparison of RL and SCOPE directional anisotropy
4. Comparison between RL and Vinnikov capabilities
4.1. The Vinnikov kernel approach
4.2. Comparison between RL and Vinnikov capabilities
5. Discussion
5.1. Limitations of the parametric approaches
5.2. Applications of RL to field and satellite data
5.2.1. Qualitative assessment of field measurements
5.2.2. Qualitative assessment of anisotropy on satellite data
5.2.3. Correction of TIR directional anisotropy on space data
6. Conclusion
References